15819x

001525

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2018-06-27

正交各向异性材料法则

任何材料满足其应力应变布置的地方，都会使用正交各向异性材料法则。对此例如纤维增强的合成材料、梯形板、配筋混凝土或者木材。

正交各向异性材料通常包含胡克定律

ν = \frac{E}{2 G} - 1 \leq 0, 5

公式 1

- 1 < ν < 0, 5

公式 2

不再有效。

横向应变

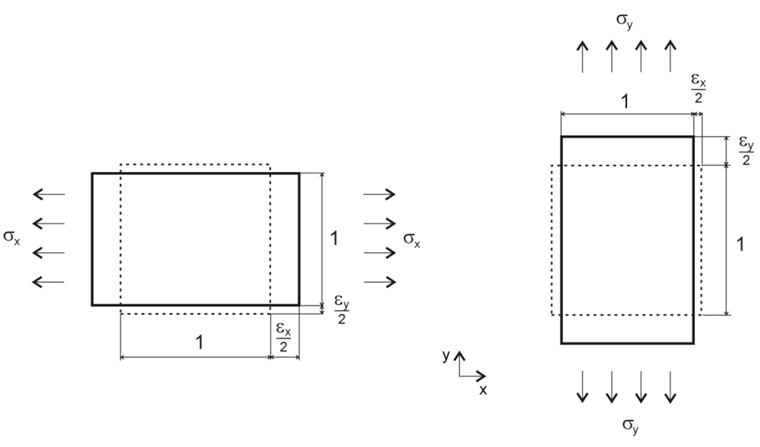
下列材料参数属于二维刚度，一般没有特别说明，指的材料是木材。基于一个局部坐标系，如图 01 所示。

E_x = 面上局部 x 方向上的刚度
E_y = 面上局部 y 方向上的刚度
G_xz = 面上局部 x 方向上的抗剪刚度（板厚度方向）
G_yz = 面上局部 y 方向上的抗剪刚度（板厚度方向）
G_xy = 板平面上的抗剪刚度
ν_xy = 在 x 方向上的横向应变
ν_yx = 在 y 方向上的横向应变

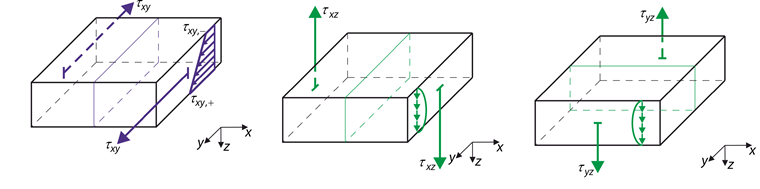
在图 02 中的应力和这里的提到的刚度相关。

剪应力

材料法则受如下的限制：

公式 1：

\frac{ν_{yx}}{E_{y}} = \frac{ν_{xy}}{E_{x}}

公式 3

公式 2：

ν_{xy} ⩾ ν_{yx}

公式 4

公式 3：

ν_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot ν_{yx}

公式 5

公式 4（在板平面上的刚度）：

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}] \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}]

公式 6

上述公式中的应变比强调了图 01 中的关系。

计算在板平面上的刚度如下。

公式 5：

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix}]

公式 7

横向应变 ν

如在图 01 中所解释的，在该方向上改变的变形和应力是由相应方向上更平滑的材料行为引起的。

应变比：

公式 6：

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

公式 8

公式 7：

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

公式 9

关于技术提问和解答：

σ_{x} \neq 0, σ_{y} = 0, σ_{xy} = 0

公式 10

下列公式是根据胡克定律得出的。

公式 8：

ε_{x} = \frac{σ_{x}}{E_{x}}

公式 11

公式 9：

ε_{y} = \frac{σ_{y}}{E_{y}}

公式 12

公式 10：

σ_{y} = ε_{y} \cdot E_{y} mit E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

公式 13

公式 11：

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

公式 14

公式 12：

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} mit ν_{xy} = - \frac{ε_{y}}{ε_{x}}

公式 15

公式 13：

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

公式 16

刚度矩阵

计算板的整体刚度矩阵。

公式 14：

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix}]

公式 17

弯曲部分：

公式 15：

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

公式 18

公式 16：

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

公式 19

公式 17：

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

公式 20

公式 18：

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

公式 21

板壳部分：

公式 19：

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - ν_{xy} ν_{yx}}

公式 22

公式 20：

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

公式 23

公式 21：

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - ν_{xy} ν_{yx}}

公式 24

公式 22：

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

公式 25

剪切部分：

公式 23：

D_{44} = \frac{5}{6} G_{xz} \cdot d

公式 26

公式 24：

D_{55} = \frac{5}{6} G_{yz} \cdot d

公式 27

当然，这些公式的前提条件一直是刚度矩阵为正，即矩阵的所有特征值也都是正的。

出于这个原因 RFEM 根据下面的公式来检查横向应变的定义。

公式 25：

ν_{xy} \leq 0, 999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

公式 28

示例

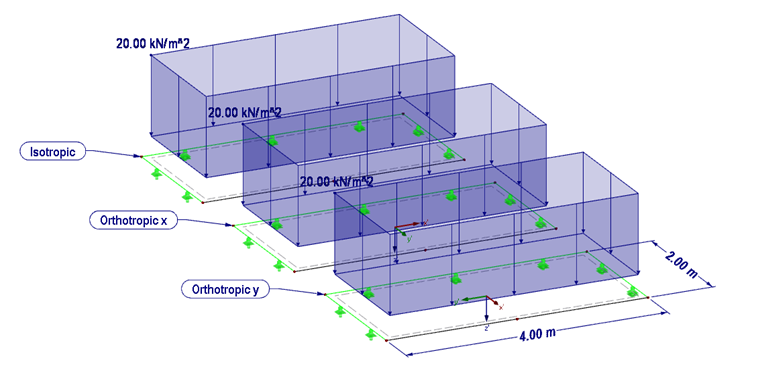
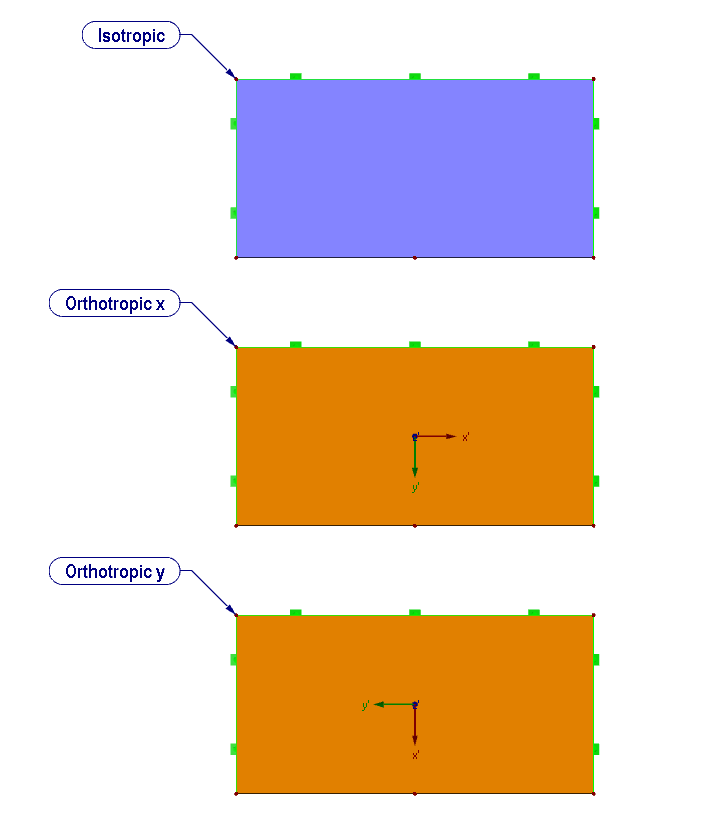
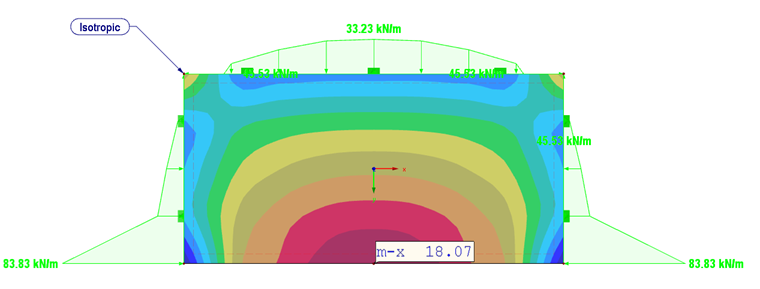
下面的示例（图 03）展示正交各向异性材料的材料行为。这里的例子，与最左边的各向异性材料比较，在右边设置了各向同性材料。并且，各向异性材料的板上设置在 x 方向上的抗剪刚度远大于 y 方向上的抗剪刚度。

系统

结构：

板厚 200mm
材料 C24
正交各向异性刚度

$\begin{array}{l} E_{x} = 1.100, 0 kN / {cm}^{2} \\ E_{y} = 37, 0 kN / {cm}^{2} \\ G_{y} = 6, 9 kN / {cm}^{2} \\ G_{x} = 69, 0 kN / {cm}^{2} \\ G_{xy} = 69, 0 kN / {cm}^{2} \\ ν_{xy} = 2, 52 \\ ν_{yx} = 0, 085 \end{array}$

公式 29
各向同性刚度

$\begin{array}{l} E = 1.100 kN / {cm}^{2} \\ G = 500 kN / {cm}^{2} \\ ν = 0, 1 \end{array}$

公式 30
尺寸 b = 2,0 m，l = 4,0 m
荷载 20 kN/m²
有限元网格尺寸 50 cm

该结构在垂直的 z 方向是固定不可移动的。对于在 x 方向和 y 方向上的支座条件，在软件中选择没有约束。

该计算基于一阶理论的线性弹性材料行为和支座条件得出。

通过上面的已知值胡克定律给出了下面的横向应变。

公式 26：

ν = (\sqrt{E_{x} \cdot E_{y}}) / (2 G) - 1 = 6, 97

公式 31

选定的材料模型无法实现这种高的横向应变。但是这些值可以通过 [1] 中的这个公式进行调整。

公式 27：

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

公式 32

公式 28：

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

公式 33

公式 29：

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1.100}{37}} = 2, 52

公式 34

公式 30：

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1.100}} = 0, 085

公式 35

面的刚度

结果:
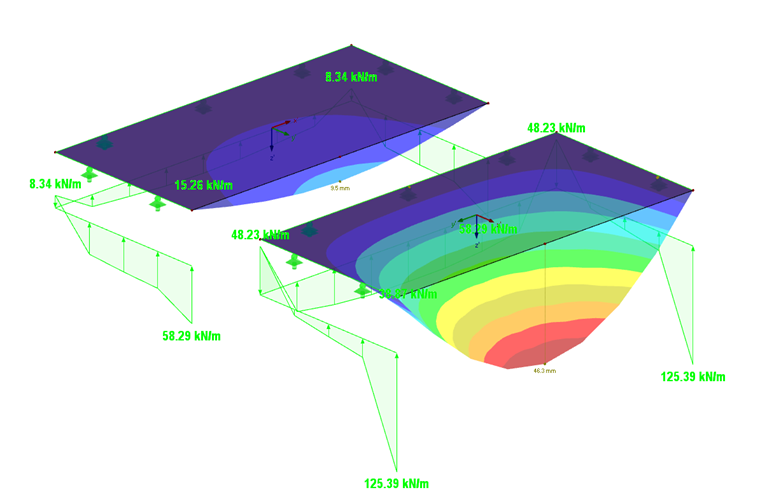
正如预期的那样，在 y 方向上的刚度产生最大的变形（图 06）。各向同性的板的支座反力和弯矩如图 05 所示。

各向同性材料的结果

由于板在 y 方向上具有高刚度 (E_y = 1.100 kN/cm²)，那么在这个方向上就具有高承载力，所以这里的支座反力也很大 (125,4 kNm 到 58,3 kNm)。

各向异性板的变形和支座反力

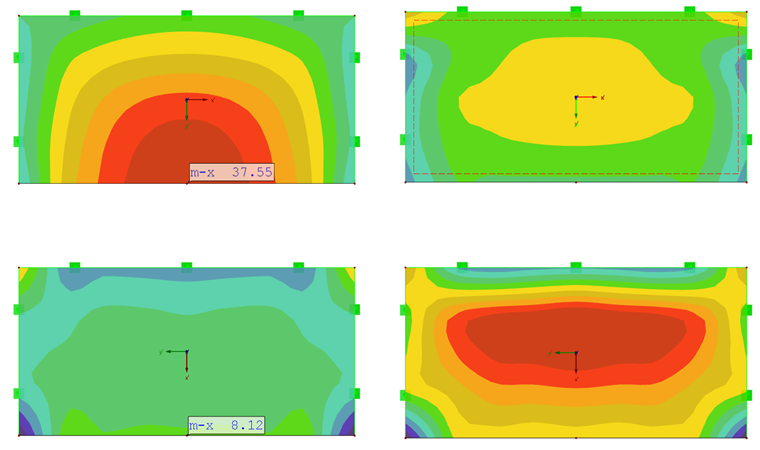
正交各向异性板中的 x 和 y 方向的最大弯矩分别为 m_x 和 m_y，在 y 方向上刚度更大。

板在 y 方向上有更大的刚度，那么最大弯矩 m_y 在板中心的附近（见图 07）。

Biegemomente der orthotropen Platte mx (links) und my (rechts)

横向应变的变量

对于强度为 C24 的材料，根据应变图，横向应变可以达到表格中所列的最大值和最小值。

	最大	最小
ν_xy	5.447	-5.447
ν_yx	0.183	-0.183

开始时引入的具有很大刚度 (E_x = 11.000) 的板在这里给它定义一个很大的横向应变。板的其它刚度保持不变。

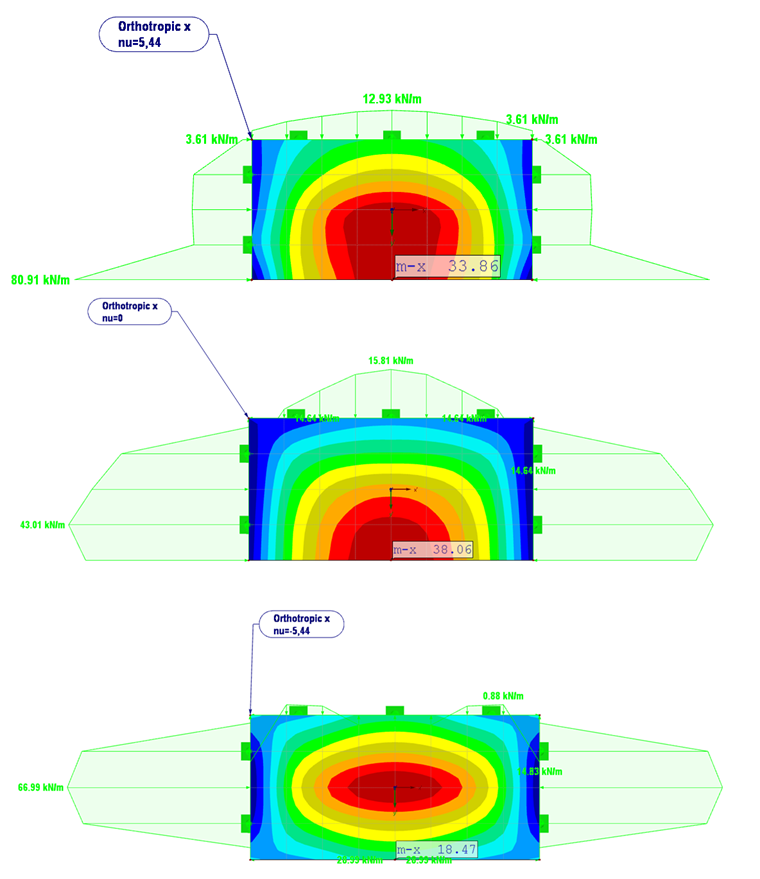
图 08 中是由 ν_xy = 5.44 到 -5.44 变量得出的结果。

对于 ν_xy = 5.44 支座反力性质上与各向同性的材料行为是相同的。弯矩从 m_x = 18.1 kNm/m (isotrope Platte) 增加到 m_x = 34.9 kNm/m（各向异性材料板）。

与具有较常见横向应变 (ν_xy = 2,5) 的正交各向异性材料板相比，弯矩有稍微变小。

Ergebnisse der Variation gemäß Tabelle (links: νxy= 5.44，中间： νxy= 0，右： νxy= -5.44）

当 ν_xy = 0 时板的自由端的支座的偏移值变为近似常量值 43 kN/m。

弯矩 m_x 增大到 38.1 kNm/m。和前面的结果 (ν_xy =5,44) 相比较这显示了横向应变的影响。对于 ν =0 横向应变没有引起变形或者应变。

当 ν_xy = -5.44 时在板的自由端出现超临界状况，支座反力为负。最大弯矩出现在板中心为 59.5 kNm/m。

现在这个板更像一个单轴拉紧的板，在它的纵向上没有第三个支座。

根据图 01 结合这里引入的关系就可以解释这种行为。

由于横向应变值为负且绝对值很大 (ν_xy = -5,44)，在板的自由端完全过压，这里不会变形。

正交各向异性在 y 方向上的影响在这里接近零 (E_y ≈ 0)。

概述总结

利用 RFEM 中的正交各向材料模型几乎可以对任何材料参数进行定义。基于横向应变的变量可以得出非常不同的结果。按照 [1] 中进行数值修改过的横向应变得出一个接近单跨梁的解。

公式 31：

M_{y} = \frac{q l^{2}}{8} = 40 kNm

公式 36

过高的负的横向应变表示一个修改的静力学系统，这不在与建模相关。

作者

Kuhn 先生负责木结构产品的开发工作，并为客户提供技术支持。

链接

结构非线性分析软件

参考

Huber, M. T : The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

下载

;