16131x

001525

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

27.6.2018

Ortotropní materiálové modely

Ortotropní materiálové modely se uplatňují všude tam, kde jsou materiály uspořádány podle svého namáhání. Příkladem jsou plasty zesílené vlákny, trapézové plechy, vyztužený beton nebo dřevo.

Pro ortotropní materiály již obvykle používaný Hookův zákon

u = \frac{E}{2 G} - 1 \leq 0, 5

Vzorec 1

- 1 < u < 0, 5

Vzorec 2

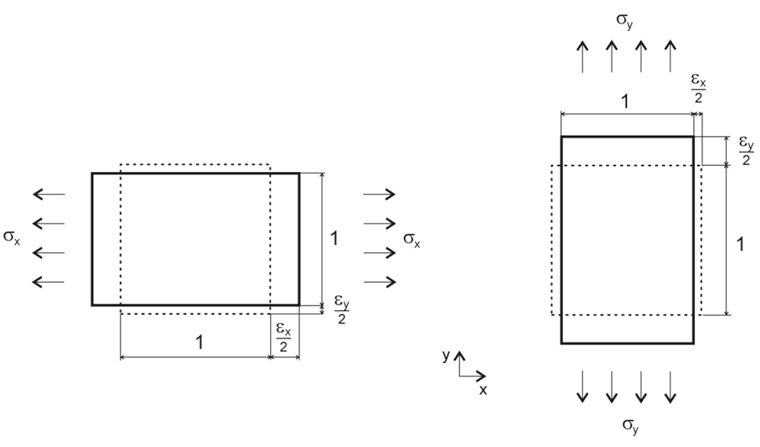
není platný.

Příčné protažení

Následující materiálové parametry se vztahují na dvourozměrnou tuhost a, pokud není uvedeno jinak, na materiál dřevo. Jako základ stanovíme lokální osový systém, který je znázorněn na obr. 01.

E_x = tuhost v lokálním směru x plochy
E_y = tuhost v lokálním směru y plochy
G_xz = tuhost ve smyku v lokálním směru x plochy (směr tloušťky desky)
G_yz = tuhost ve smyku v lokálním směru y plochy (směr tloušťky desky)
G_xy = tuhost ve smyku v rovině desky
ν_xy = příčné protažení ve směru x
ν_yx = příčné protažení ve směru y

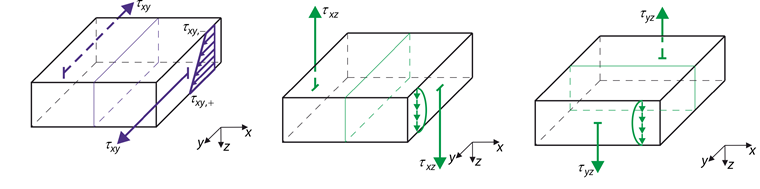
Napětí znázorněná na obr. 02 se vztahují k výše uvedeným tuhostem.

Smyková napětí

Materiálový model stanovuje následující pravidla.

Rovnice 1:

\frac{ν_{yx}}{E_{y}} = \frac{ν_{xy}}{E_{x}}

Vzorec 3

Rovnice 2:

ν_{xy} ⩾ ν_{yx}

Vzorec 4

Rovnice 3:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot ν_{yx}

Vzorec 5

Rovnice 4 (tuhosti v rovině desky):

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}] \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}]

Vzorec 6

Poměr protažení ve výše uvedených rovnicích podtrhuje vztahy na obr. 01.

Tuhosti v rovině desky se vypočítají následovně.

Rovnice 5:

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix}]

Vzorec 7

Příčné protažení ν

Jak je již zřejmé z obrázku 01, vlivem měkčích vlastností materiálu v daném směru se mění deformace a napětí v příslušném směru.

Poměr protažení:

Rovnice 6:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

Vzorec 8

Rovnice 7:

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

Vzorec 9

Krátký dotaz - rychlá odpověď:

σ_{x} e q 0, σ_{y} = 0, σ_{xy} = 0

Vzorec 10

z toho plynou následující rovnice podle Hookova zákona.

Rovnice 8:

ε_{x} = \frac{σ_{x}}{E_{x}}

Vzorec 11

Rovnice 9:

ε_{y} = \frac{σ_{y}}{E_{y}}

Vzorec 12

Rovnice 10:

σ_{y} = ε_{y} \cdot E_{y} kde E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

Vzorec 13

Rovnice 11:

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

Vzorec 14

Rovnice 12:

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} kde ν_{xy} = - \frac{ε_{y}}{ε_{x}}

Vzorec 15

Rovnice 13:

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

Vzorec 16

Matice tuhosti

Výpočet globální matice tuhosti desky

Rovnice 14:

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix}]

Vzorec 17

Ohybové složky:

Rovnice 15:

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Vzorec 18

Rovnice 16:

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

Vzorec 19

Rovnice 17:

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Vzorec 20

Rovnice 18:

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

Vzorec 21

Membránové složky:

Rovnice 19:

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - ν_{xy} ν_{yx}}

Vzorec 22

Rovnice 20:

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

Vzorec 23

Rovnice 21:

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - ν_{xy} ν_{yx}}

Vzorec 24

Rovnice 22:

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

Vzorec 25

Smykové složky:

Rovnice 23:

D_{44} = \frac{5}{6} G_{xz} \cdot d

Vzorec 26

Rovnice 24:

D_{55} = \frac{5}{6} G_{yz} \cdot d

Vzorec 27

Předpokladem platnosti těchto rovnic je samozřejmě kladná matice tuhosti, tj. všechna vlastní čísla matice jsou kladná.

RFEM proto mimo jiné ověří zadání příčného protažení pomocí následující rovnice.

Rovnice 25:

ν_{xy} \leq 0, 999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Vzorec 28

Příklad použití

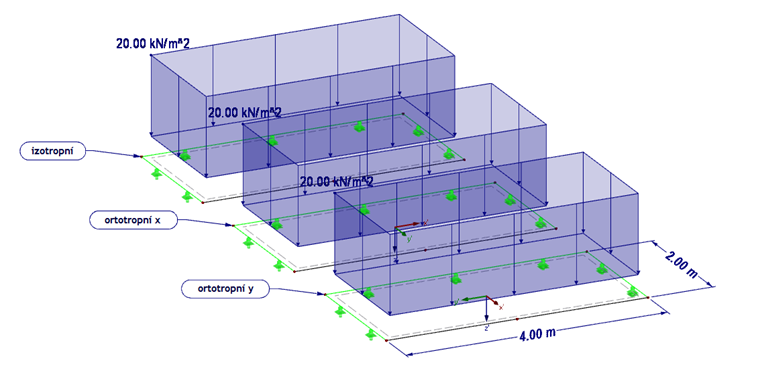
Na následujícím příkladu (obr. 03) si vysvětlíme ortotropní chování materiálu. Porovnáme přitom ortotropní materiál s izotropním materiálem. U ortotropní desky navíc zadáme vysokou tuhost jednou ve směru x a podruhé ve směru y.

Systém

Konstrukce:

Tloušťka desky 200 mm
Materiál C24
Ortotropní tuhosti

$\begin{array}{l} E_{x} = 1100, 0 kN / {cm}^{2} \\ E_{y} = 37, 0 kN / {cm}^{2} \\ G_{y} = 6, 9 kN / {cm}^{2} \\ G_{x} = 69, 0 kN / {cm}^{2} \\ G_{xy} = 69, 0 kN / {cm}^{2} \\ u_{xy} = 2, 52 \\ u_{yx} = 0, 085 \end{array}$

Vzorec 29
Izotropní tuhosti

$\begin{array}{l} E = 1100 kN / {cm}^{2} \\ G = 500 kN / {cm}^{2} \\ u = 0, 1 \end{array}$

Vzorec 30
Rozměry b = 2,0 m, l = 4,0 m
Zatížení 20 kN/m²
Velikost sítě konečných prvků 50 cm

Podepření konstrukce zamezuje posunu ve svislém směru z. Podporové podmínky ve směru x a y byly zvoleny tak, aby nedocházelo k žádným vynuceným přetvořením.

Výpočet proběhne podle teorie prvního řádu se zohledněním lineárně pružného chování materiálu a příslušných podporových podmínek.

Podle Hookova zákona se pro zadané hodnoty stanoví následující příčné protažení.

Rovnice 26:

ν = (\sqrt{E_{x} \cdot E_{y}}) / (2 G) - 1 = 6, 97

Vzorec 31

Takto vysoké příčné protažení není v případě zvoleného materiálového modelu možné. Pomocí rovnic z [1] lze ovšem hodnoty upravit.

Rovnice 27:

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Vzorec 32

Rovnice 28:

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

Vzorec 33

Rovnice 29:

ν_{xy} = (\frac{\sqrt{1100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1100}{37}} = 2, 52

Vzorec 34

Rovnice 30:

ν_{xy} = (\frac{\sqrt{1100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1100}} = 0, 085

Vzorec 35

Plochy s příslušnými tuhostmi

Výsledky:
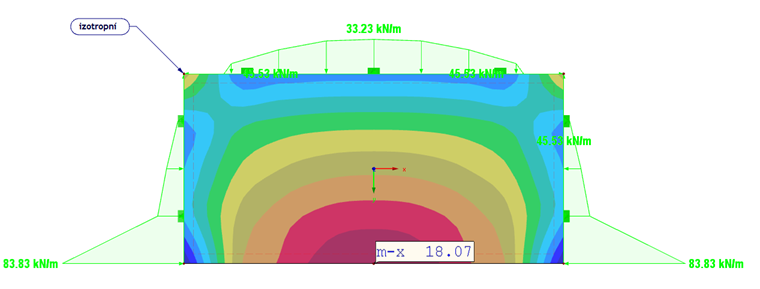
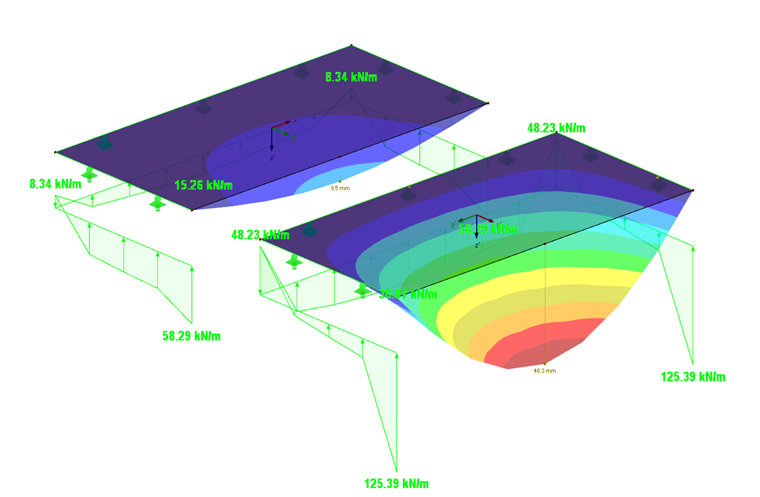
Podle očekávání vycházejí největší výsledné deformace, pokud jsou tuhosti orientovány ve směru y (obr. 06). Podporové reakce a moment v izotropní desce jsou znázorněny na obr. 05.

Výsledky izotropního materiálu

Vzhledem k tomu, že deska s vysokou tuhostí ve směru y (E_y = 1100 kN/cm²) vykazuje v tomto směru vysokou únosnost, jsou tu také reakce vyšší (125,4 kNm ku 58,3 kNm).

Deformace a podporové reakce u ortotropních desek

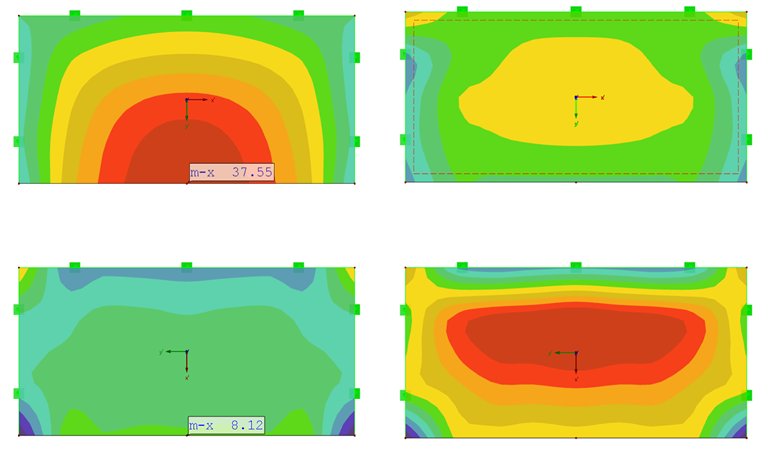
Maximální ohybové momenty jsou u ortotropních desek obdobné v případě m_x s tuhostí ve směru x a v případě m_y s vyšší tuhostí ve směru y.

Deska s vysokou tuhostí ve směru y vykazuje maximální ohybový moment m_y téměř ve svém středu (obr. 07).

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Variabilita příčného protažení

Příčné protažení může podle vztahů pro přetvoření u materiálu s pevností C24 dosahovat maximálních a minimálních hodnot uvedených v tabulce.

	Max.	Min.
ν_xy	5,447	-5,447
ν_yx	0,183	-0,183

První definovaná deska s vysokou tuhostí (E_x = 11 000) se proto zadá s danými vysokými hodnotami příčného protažení. Ostatní tuhosti ovšem u desky zůstávají beze změny.

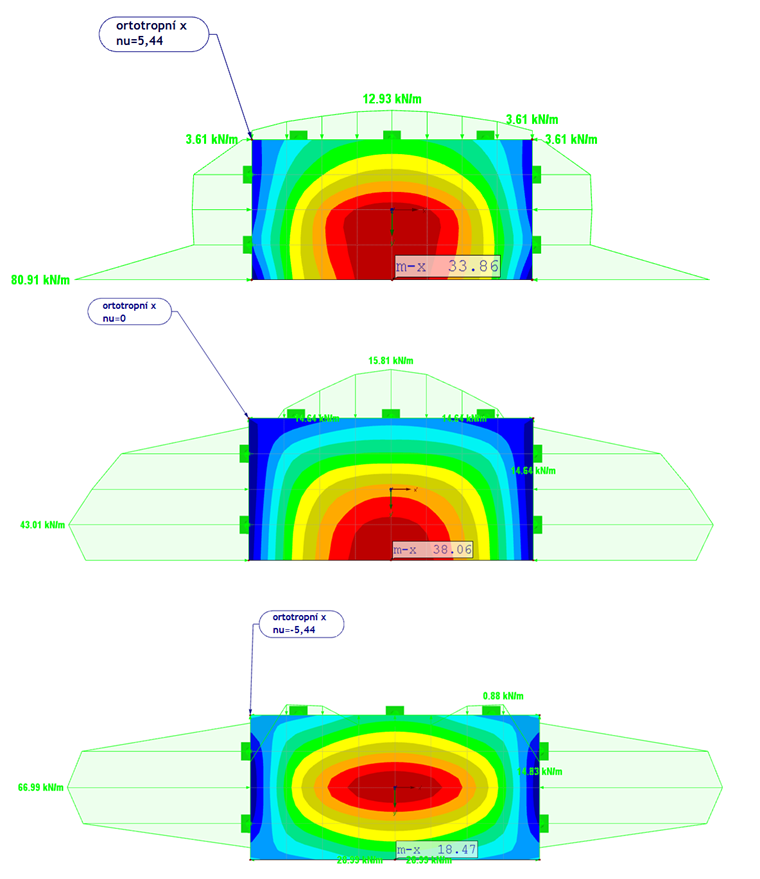
Na obr. 08 jsou uvedeny výsledky pro rozsah ν_xy od 5,44 do -5,44 .

V případě ν_xy = 5,44 reakce kvalitativně odpovídají izotropnímu chování materiálu. Ohybový moment roste od m_x = 18,1 kNm/m (izotropní deska) do m_x = 34,9 kNm/m (ortotropní deska).

Oproti ortotropní desce s obvyklým příčným protažením (ν_xy = 2,5) se ohybový moment lehce snižuje.

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, uprostřed: νxy = 0, vpravo: νxy = -5,44)

Při ν_xy = 0 se vysoká hodnota podporové reakce na volném konci desky rozloží do konstatní hodnoty 43 kN/m.

Moment m_x se zvýší na 38,1 kNm/m. Ve srovnání s předchozím výsledkem (ν_xy =5,44) se tu projevuje vliv příčného protažení. Při ν =0 nevzniká žádná deformace ani přetvoření v důsledku příčného protažení.

V případě ν_xy = -5,44 dochází k porušení na volném konci desky a podporové reakce přecházejí do záporných hodnot. Maximální moment, který dosahuje 59,5 kNm/m, lze pozorovat ve středu desky.

Deska se nyní chová spíše jako deska nosná v jednom směru bez třetí podpory ve svém podélném směru.

Na obr. 01 a zde znázorněných vztazích si můžeme toto chování vysvětlit.

Kvůli vysokému zápornému příčnému protažení (ν_xy = -5,44) je deska na volném okraji zcela přetížena, a nemůže se proto deformovat.

Vliv ortotropie ve směru y je přitom téměř nulový (E_y ≈ 0).

Shrnutí

Ortotropní materiálový model v programu RFEM umožňuje zadat takřka libovolné parametry materiálů. V důsledku variability příčného protažení můžeme dosáhnout značně odlišných výsledků. Příčné protažení po úpravě hodnot podle [1] vede k hodnotám, které se blíží řešení u prostého nosníku.

Rovnice 31:

M_{y} = \frac{q l^{2}}{8} = 40 kNm

Vzorec 36

Příliš vysoká záporná příčná protažení poukazují na upravený statický systém, který již neodpovídá příslušnému modelu.

Autor

Ing. Kuhn je zodpovědný za vývoj produktů pro dřevěné konstrukce a poskytuje technickou podporu zákazníkům.

Odkazy

Software pro nelineární analýzu

Reference

Huber, M. T : The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

Stahování

Model 1 v programu RFEM

472 KB

Model 2 v programu RFEM

460 KB

;