Voltar para a base de dados de conhecimento

15819x

001525

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2018-06-27

Leis de material ortotrópico

As leis para materiais ortotrópicos são utilizadas onde os materiais são ordenados de acordo com o seu carregamento. Exemplo disso é os plásticos reforçados com fibras, chapas perfiladas, betão armado e madeira.

a lei de Hooke é geralmente incluída para materiais ortotrópicos

m a t h r m n u = f r a c m a t h r m E 2 m a t h r m G - 1 l e q 0, 5

Fórmula 1

- 1 < m a t h r m n u < 0, 5

Fórmula 2

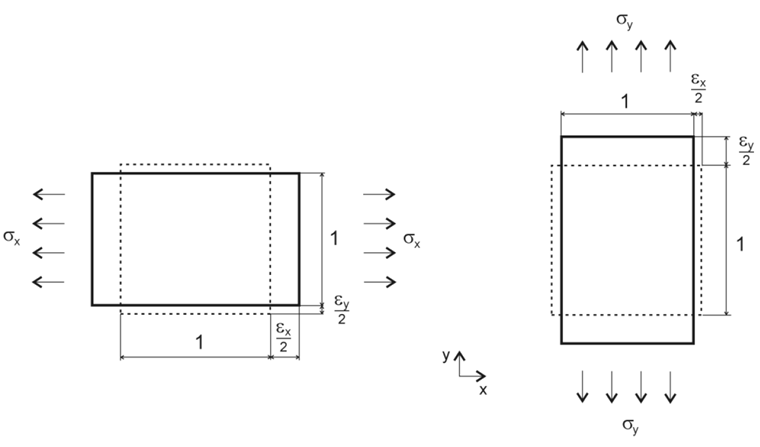
deixa de ser válida.

deformação transversal

Os seguintes parâmetros do material referem-se à rigidez bidimensional e, salvo indicação em contrário, ao material madeira. Um sistema de eixos local é a base, conforme apresentado na Figura 01.

E_x = rigidez na direção x local da superfície
E y = rigidez na direção y local da superfície
G_xz = rigidez de corte na direção x local da superfície (direção da espessura da laje)
G_yz = rigidez de corte na direção y local da superfície (direção da espessura da laje)
G_xy = área de rigidez de corte no plano
ν_xy = deformação transversal na direção x
ν_yx = deformação transversal na direção y

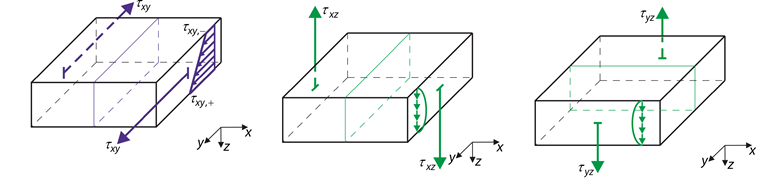
As tensões na Figura 02 estão relacionadas com as rigidezes aqui mencionadas.

tensões de corte

A lei dos materiais está sujeita às seguintes regras.

Equação 1:

\frac{ν_{yx}}{E_{y}} = \frac{ν_{xy}}{E_{x}}

Fórmula 3

Equação 2:

ν_{xy} ⩾ ν_{yx}

Fórmula 4

Equação 3:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot ν_{yx}

Fórmula 5

Equação 4 (rigidezes no plano da área):

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}] \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}]

Fórmula 6

A relação das deformações nas equações mencionadas acima destaca as relações na Figura 01.

A rigidez na área do plano é calculada como se segue.

Equação 5:

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix}]

Formel 7

Deformação transversal ν

Como explicado na Figura 01, as deformações e tensões alteradas nesta direção resultam do comportamento do material mais suave na respetiva direção.

Relação das deformações:

Equação 6:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

Fórmula 8

Equação 7:

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

Fórmula 9

Pergunta simples – resposta rápida:

{m a t h r m s i g m a}_{} m a t h r m x n e q 0, {m a t h r m s i g m a}_{} m a t h r m y = 0, {m a t h r m s i g m a}_{} m a t h r m x y = 0

Fórmula 10

as seguintes equações resultam da lei de Hooke.

Equação 8:

ε_{x} = \frac{σ_{x}}{E_{x}}

Fórmula 11

Equação 9:

ε_{y} = \frac{σ_{y}}{E_{y}}

Fórmula 12

Equação 10:

σ_{y} = ε_{y} \cdot E_{y} mit E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

Fórmula 13

Equação 11:

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

Fórmula 14

Equação 12:

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} mit ν_{xy} = - \frac{ε_{y}}{ε_{x}}

Fórmula 15

Equação 13:

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

Fórmula 16

Matriz de rigidez

Cálculo da matriz de rigidez global da placa.

Equação 14:

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix}]

Fórmula 17

Componentes de flexão:

Equação 15:

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Fórmula 18

Equação 16:

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

Fórmula 19

Equação 17:

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Fórmula 20

Equação 18:

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

Fórmula 21

Componentes de membrana:

Equação 19:

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - ν_{xy} ν_{yx}}

Fórmula 22

Equação 20:

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

Fórmula 23

Equação 21:

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - ν_{xy} ν_{yx}}

Fórmula 24

Equação 22:

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

Fórmula 25

Componentes de corte:

Equação 23:

D_{44} = \frac{5}{6} G_{xz} \cdot d

Fórmula 26

Equação 24:

D_{55} = \frac{5}{6} G_{yz} \cdot d

Fórmula 27

Um pré-requisito para estas equações é que a matriz de rigidez seja definida como positiva, isto é, que todos os valores próprios da matriz sejam positivos.

Por esta razão, o RFEM verifica, entre outras coisas, a definição da extensão transversal de acordo com a seguinte equação.

Equação 25:

ν_{xy} \leq 0, 999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Fórmula 28

Exemplo

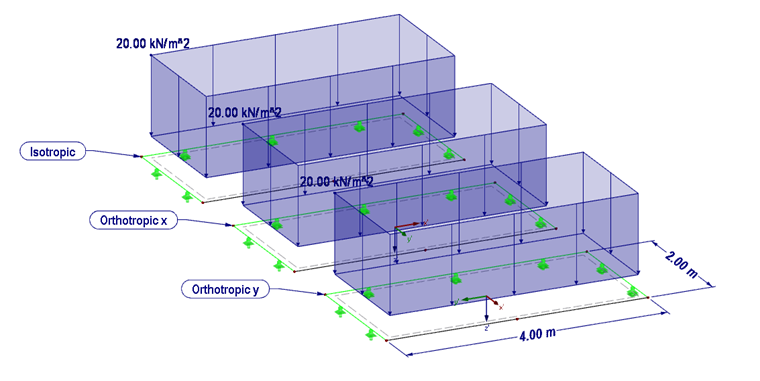
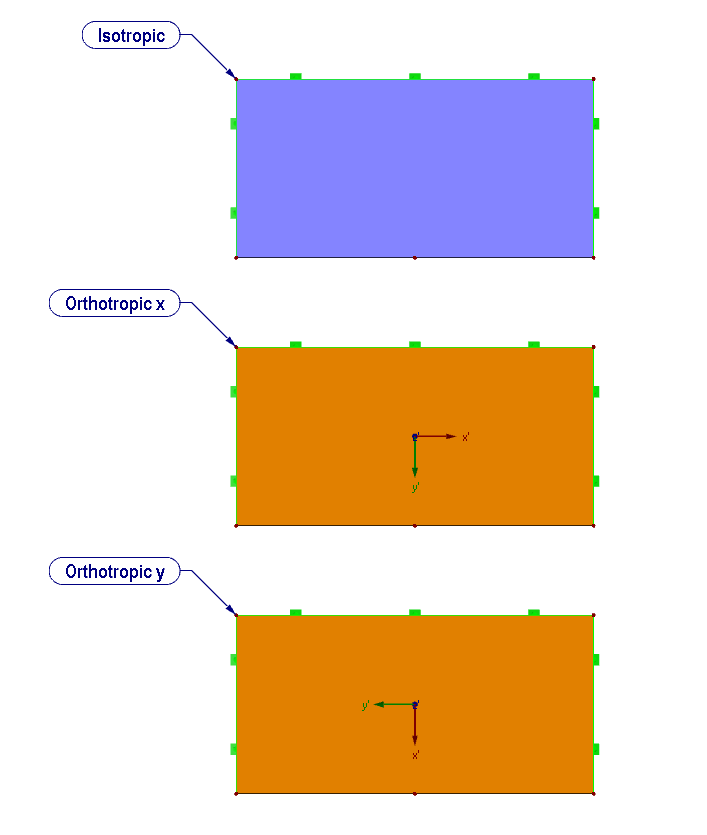
O comportamento do material ortotrópico será explicado com base no seguinte exemplo (Figura 03). Um material ortotrópico será comparado com um material isotrópico. Além disso, a rigidez da placa ortotrópica será definida com a rigidez elevada nas direções x e na direção y.

Sistema

Estrutura:

Espessura da placa 200 mm
Material C 24
Rigidezes ortotrópicas

$\begin{array}{l} E_{x} = 1.100, 0 kN / {cm}^{2} \\ E_{y} = 37, 0 kN / {cm}^{2} \\ G_{y} = 6, 9 kN / {cm}^{2} \\ G_{x} = 69, 0 kN / {cm}^{2} \\ G_{xy} = 69, 0 kN / {cm}^{2} \\ ν_{xy} = 2, 52 \\ ν_{yx} = 0, 085 \end{array}$

Fórmula 29
Rigidezes isotrópicas

$\begin{array}{l} E = 1.100 kN / {cm}^{2} \\ G = 500 kN / {cm}^{2} \\ ν = 0, 1 \end{array}$

Fórmula 30
Dimensão w = 2,0 m, l = 4,0 m
Carga 20 kN/m²
Tamanho da malha de EF 50 cm

A estrutura é suportada como fixada de forma rígida na direção vertical z. As condições de apoio nas direções x e y foram selecionadas de tal forma que não ocorrem efeitos devido à restrição.

O cálculo é realizado de acorco com a análise estática linear com comportamento de material elástico linear e condições de apoio.

A seguinte deformação transversal resulta da lei de Hooke, em conjunto com os valores dados.

Equação 26:

ν = (\sqrt{E_{x} \cdot E_{y}}) / (2 G) - 1 = 6, 97

Fórmula 31

Esta deformação transversal elevada não é possível com o modelo de material selecionado. Com as equações de [1] , os valores podem, contudo ser ajustados.

Equação 27:

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Fórmula 32

Equação 28:

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

Fórmula 33

Equação 29:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1.100}{37}} = 2, 52

Fórmula 34

Equação 30:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1.100}} = 0, 085

Fórmula 35

Superfícies com rigidez

Resultados:
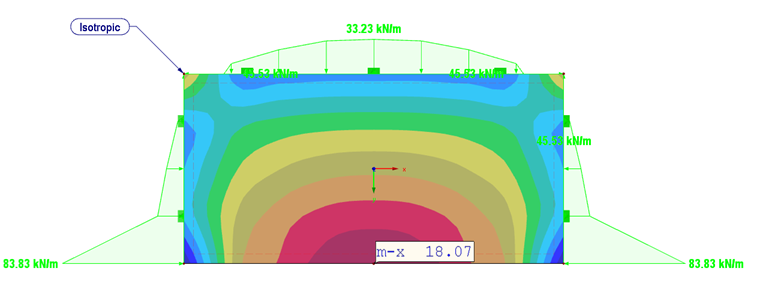
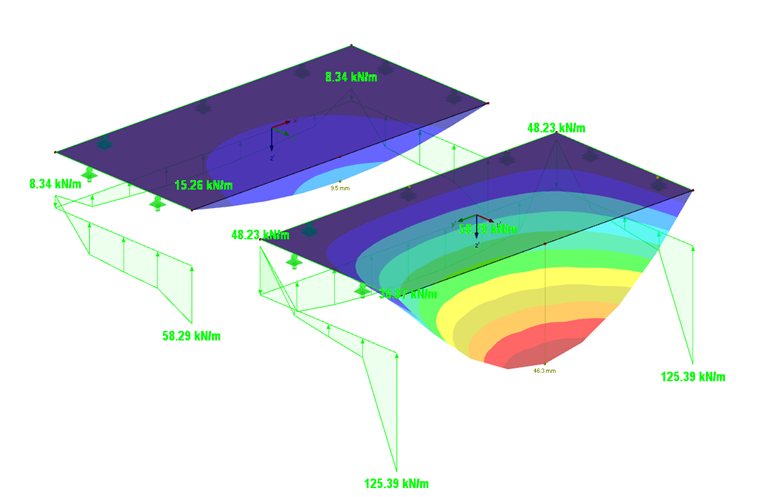
Conforme esperado, as maiores deformações ocorrem com a orientação da rigidez na direção y (Figura 06). A reação de apoio e o momento da placa isotrópica são apresentados na Figura 05.

Resultados de material isotrópico

a placa com rigidez elevada na direção y (E_y = 1100 kN/cm²) tem resistência elevada nesta direção, as reações de apoio também são mais altas (125,4 kNm em comparação com 58,3 kNm).

Deformações e reações de apoio de placas ortotrópicas

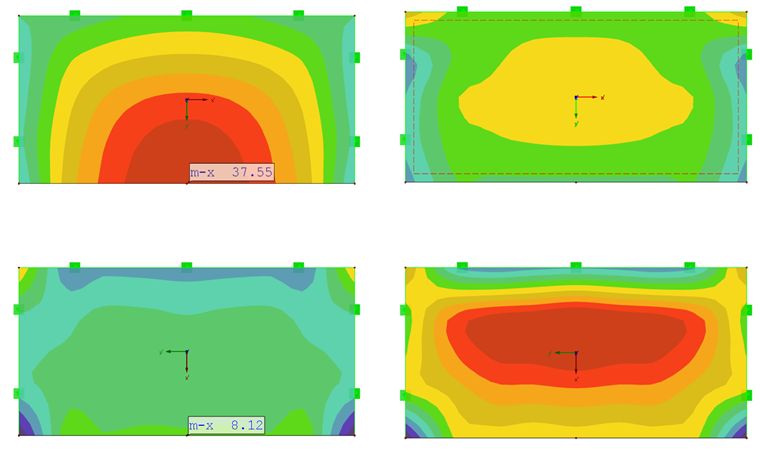
Os momentos de flexão máximos resultantes para as placas ortotrópicas são iguais para m_x com a rigidez na direção x e para m_y com uma rigidez elevada na direção y.

Para a laje com rigidez elevada na direção y, o momento fletor máximo m_y encontra-se quase no centro da laje (Figura 07).

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Variação da deformação transversal

A deformação transversal de acordo com os diagramas de deformação pode atingir os valores máximo e mínimo listados na tabela para um material de resistência C24.

	Máx	Mín
_νxy	5,447	-5,447
_νyx	0,183	-0,183

A placa introduzida no início com a rigidez elevada (E_x = 11 000) será definida com estas deformações transversais elevadas para este propósito. As outras rigidezes da laje, no entanto, permanecem inalteradas.

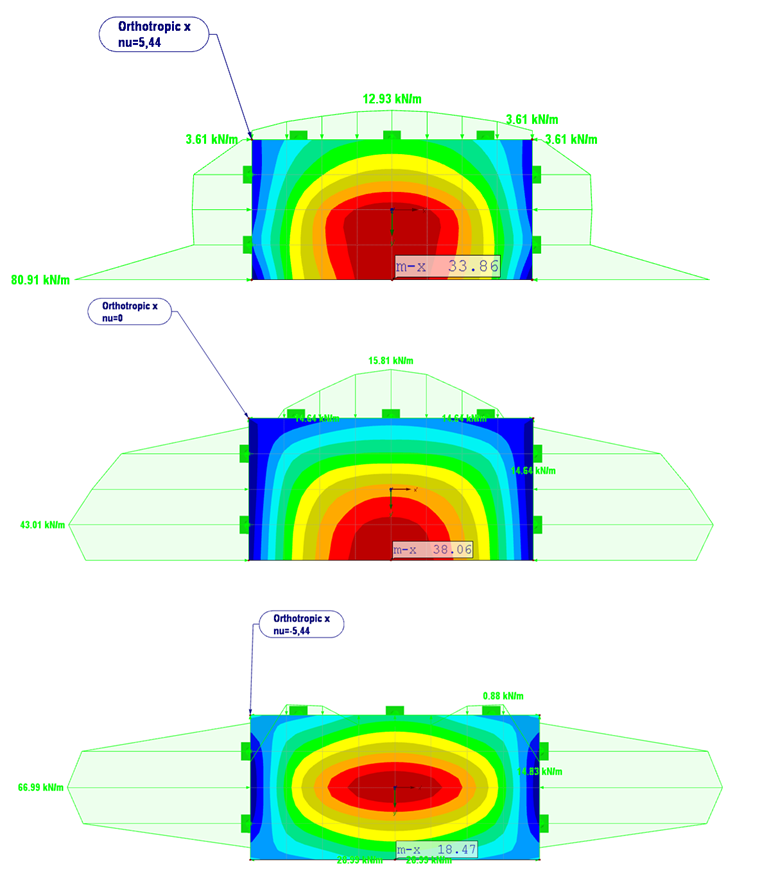
A Figura 08 mostra os resultados da variação de ν_xy = 5,44 até -5,44.

Para ν_xy = 5,44, as reações de apoio são qualitativamente idênticas ao comportamento do material isotrópico. O momento fletor aumenta de m_x = 18,1 kNm/m (placa isotrópica) para m_x = 34,9 kNm/m (placa ortotrópica).

Em comparação com a placa ortotrópica com deformações transversais comuns (ν_xy = 2,5), o momento fletor é ligeiramente reduzido.

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, meio: νxy = 0, direita: νxy = -5,44)

Com ν_xy = 0, a amplitude alta da reação de apoio na extremidade livre da placa é deslocada para um valor constante de 43 kN/m.

O momento m_x aumenta para 38,1 kNm/m. Comparada com o resultado anterior (ν_xy =5,44), a influência da deformação transversal é apresentada aqui. Para ν =0, não é causada qualquer deformação ou distorção devido à extensão transversal.

Para ν_xy = -5,44, ocorre uma rotura pós-crítica na extremidade da placa livre e as reações de apoio tornam-se negativas. O momento máximo ocorre com 59,5 kNm/m no centro da placa.

A placa agora comporta-se mais do que uma placa sujeita a tensão uniaxial, sem o terceiro apoio na direção longitudinal.

Este comportamento pode ser explicado com base na Figura 01 e na relação aí listada.

Devido à elevada deformação transversal negativa (ν_xy = -5,44), a placa está completamente comprimida na borda livre e, portanto, não pode ser deformada.

A influência da ortotropia na direção_y é quase nula aqui (Ey ≈ 0).

Conclusão

Quase todos os parâmetros de material podem ser definidos com o modelo de material ortotrópico no RFEM. São possíveis resultados muito diferentes com a variação das deformações transversais. Uma deformação transversal após a modificação dos valores de acordo com [1] resulta em valores que se encontram próximos da solução para uma viga de vão único.

Equação 31:

M_{y} = \frac{q l^{2}}{8} = 40 kNm

Fórmula 36

As deformações transversais negativas demasiado elevadas indicam um sistema estrutural alterado que já não corresponde à modelação.

Autor

O Eng. Kuhn é responsável pelo desenvolvimento de produtos e pela garantia de qualidade da área das estruturas de madeira e providencia apoio técnico aos nossos clientes.

Ligações

Software para análises não lineares

Referências

Huber, M. T : The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

Downloads

Ficheiro de modelo 1 do RFEM

472 KB

Ficheiro de modelo 2 do RFEM

460 KB

;