Volver a la base de datos de conocimientos

15819x

001525

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2018-06-27

Leyes de los materiales ortótropos

Las leyes de materiales ortótropos se utilizan siempre que se disponen los materiales según su carga. Los ejemplos incluyen plásticos reforzados con fibra, láminas trapezoidales, hormigón armado y madera.

La ley de Hooke generalmente se incluye para materiales ortótropos

ν = \frac{E}{2 G} - 1 \leq 0, 5

Fórmula 1

- 1 < ν < 0, 5

Fórmula 2

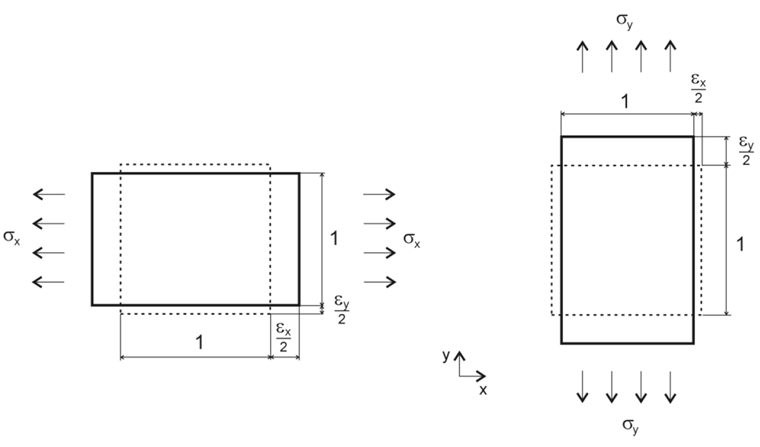
ya no es válido.

deformación transversal

Los siguientes parámetros del material se refieren a rigideces bidimensionales y, a menos que se indique lo contrario, al material de la madera. Un sistema de ejes local es la base, como se muestra en la figura 01.

E_x = rigidez en la dirección local x de la superficie
Ey = rigidez en la dirección local y de la superficie
G_xz = rigidez a cortante en la dirección local x de la superficie (dirección de la rigidez de la chapa)
G_yz = rigidez a cortante en la dirección local y de la superficie (dirección de la rigidez de la chapa)
G_xy = rigidez a cortante en el área de la chapa
ν_xy = deformación transversal en la dirección x
ν_yx = deformación transversal en la dirección y

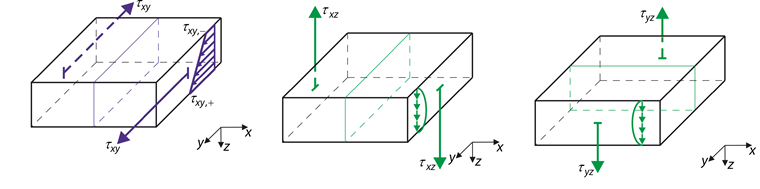
Las tensiones en la figura 02 están relacionadas con las rigideces aquí mencionadas.

Tensiones tangenciales

Esta ley del material está sujeta a las siguientes reglas.

Ecuación 1:

\frac{ν_{yx}}{E_{y}} = \frac{ν_{xy}}{E_{x}}

Fórmula 3

Ecuación 2:

ν_{xy} ⩾ ν_{yx}

Fórmula 4

Ecuación 3:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot ν_{yx}

Fórmula 5

Ecuación 4 (rigidez en el área de la chapa)

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}] \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}]

Fórmula 6

En las ecuaciones mencionadas anteriormente, la relación de las deformaciones subrayan las relaciones en la figura 01.

Las rigideces en el área en el plano se calculan como sigue.

Ecuación 5:

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix}]

Fórmula 7

Deformación transversal ν

Como se ha explicado en la figura 01, las deformaciones y tensiones modificadas en esta dirección se obtienen desde el comportamiento más suave del material en la dirección respectiva.

Razón de las deformaciones:

Ecuación 6:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

Fórmula 8

Ecuación 7:

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

Fórmula 9

Para

σ_{x} \neq 0, σ_{y} = 0, σ_{xy} = 0

Fórmula 10

las siguientes ecuaciones resultan con la ley de Hooke.

Ecuación 8:

ε_{x} = \frac{σ_{x}}{E_{x}}

Fórmula 11

Ecuación 9:

ε_{y} = \frac{σ_{y}}{E_{y}}

Fórmula 12

Ecuación 10:

σ_{y} = ε_{y} \cdot E_{y} con E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

Fórmula 13

Ecuación 11:

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

Fórmula 14

Ecuación 12:

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} con ν_{xy} = - \frac{ε_{y}}{ε_{x}}

Fórmula 15

Ecuación 13:

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

Fórmula 16

matriz de rigidez

Cálculo de la matriz de rigidez global de la chapa.

Ecuación 14:

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix}]

Fórmula 17

Componentes de flexión:

Ecuación 15:

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Fórmula 18

Ecuación 16:

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

Fórmula 19

Ecuación 17:

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Fórmula 20

Ecuación 18:

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

Fórmula 21

Componentes de la membrana:

Ecuación 19:

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - ν_{xy} ν_{yx}}

Fórmula 22

Ecuación 20:

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

Fórmula 23

Ecuación 21:

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - ν_{xy} ν_{yx}}

Fórmula 24

Ecuación 22:

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

Fórmula 25

Componentes de cortante:

Ecuación 23:

D_{44} = \frac{5}{6} G_{xz} \cdot d

Fórmula 26

Ecuación 24:

D_{55} = \frac{5}{6} G_{yz} \cdot d

Fórmula 27

Como requisito previo, la matriz de rigidez se define positiva, de forma que todos los valores propios de la matriz son positivos.

Por esta razón, RFEM comprueba, entre otras cosas, la definición de la deformación transversal según la siguiente ecuación.

Ecuación 25:

ν_{xy} \leq 0, 999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Fórmula 28

Ejemplo

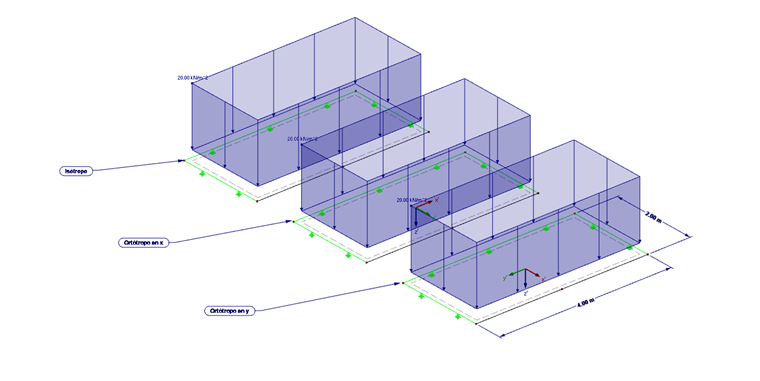
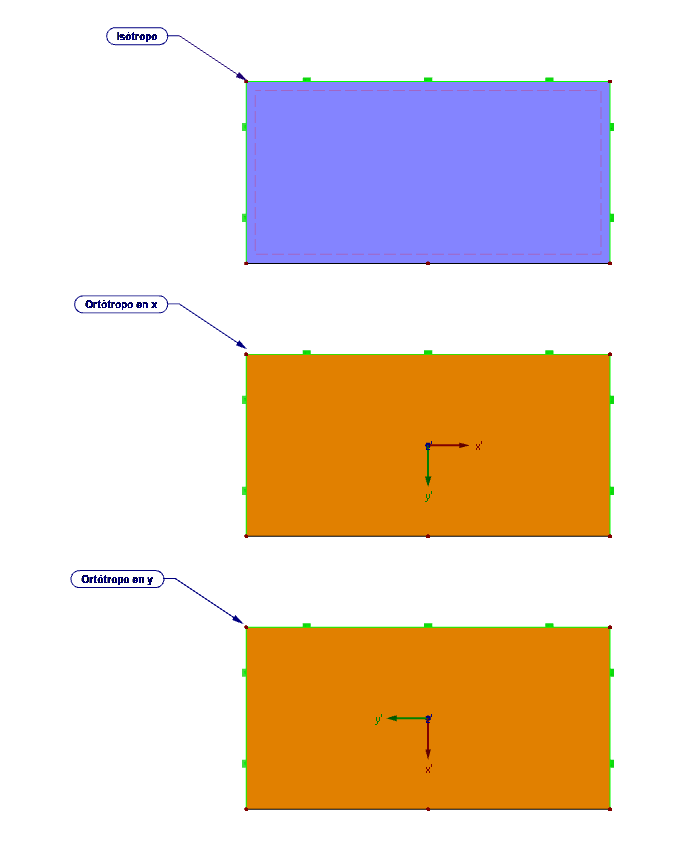
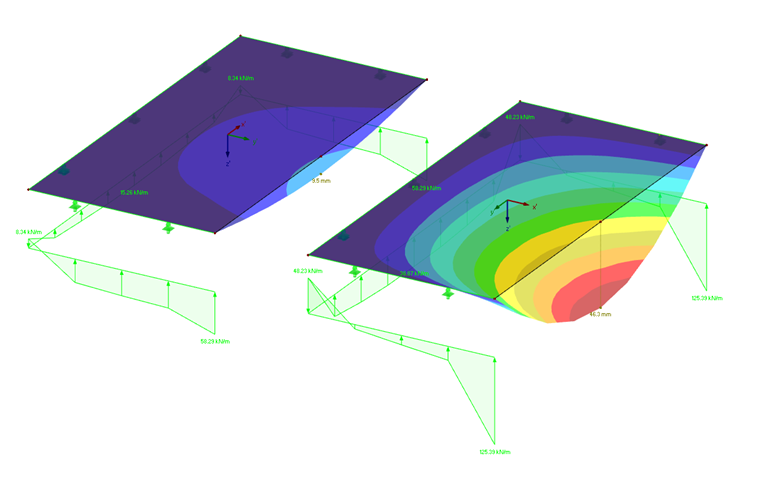
El comportamiento del material ortótropo se explicará con el siguiente ejemplo (figura 03). Se va a comparar un material ortótropo con un material isótropo. Además, la rigidez de la placa ortótropa se definirá con la rigidez alta en la dirección x y en la dirección y.

Sistema

Estructura:

Espesor de la chapa 200 mm
Material C 24
Rigidez ortótropa

$\begin{array}{l} E_{x} = 1.100, 0 kN / {cm}^{2} \\ E_{y} = 37, 0 kN / {cm}^{2} \\ G_{y} = 6, 9 kN / {cm}^{2} \\ G_{x} = 69, 0 kN / {cm}^{2} \\ G_{xy} = 69, 0 kN / {cm}^{2} \\ ν_{xy} = 2, 52 \\ ν_{yx} = 0, 085 \end{array}$

Fórmula 29
Rigidez isótropa

$\begin{array}{l} E = 1.100 kN / {cm}^{2} \\ G = 500 kN / {cm}^{2} \\ ν = 0, 1 \end{array}$

Fórmula 30
Dimensión 2 = 2,0 m, l = 4,0 m
Carga 20 kN/m²
Tamaño de la malla de EF 50 cm

La estructura está apoyada como rígidamente fijada en la dirección vertical z. Las condiciones del apoyo en las direcciones x e y se han seleccionado de tal manera que no se produzcan efectos debido a la coacción.

El cálculo se realiza según el análisis estático lineal con el comportamiento elástico lineal del material y las condiciones del apoyo.

La siguiente deformación transversal resulta de la ley de Hooke, junto con los valores dados.

Ecuación 26:

ν = (\sqrt{E_{x} \cdot E_{y}}) / (2 G) - 1 = 6, 97

Fórmula 31

Esta alta deformación transversal es imposible con el modelo de material seleccionado. Con las ecuaciones de [1], sin embargo, se pueden ajustar los valores.

Ecuación 27:

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Fórmula 32

Ecuación 28:

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

Fórmula 33

Ecuación 29:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1.100}{37}} = 2, 52

Fórmula 34

Ecuación 30:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1.100}} = 0, 085

Fórmula 35

Superficies con rigideces

Resultados:
Como se esperaba, las deformaciones más grandes ocurren con la orientación de las rigideces en la dirección y (figura 06). La reacción en el apoyo y el momento de la chapa isótropa se muestran en la figura 05.

Resultados del material isótropo

Desde que la chapa con la rigidez elevada en la dirección y (E_y = 1 100 kN/cm²) tiene la mayor resistencia en esta dirección, las reacciones en los apoyos también son mayores ahí (125,4 kNm comparado con 58,3 kNm).

Deformaciones y reacciones en los apoyos de las chapas ortótropas

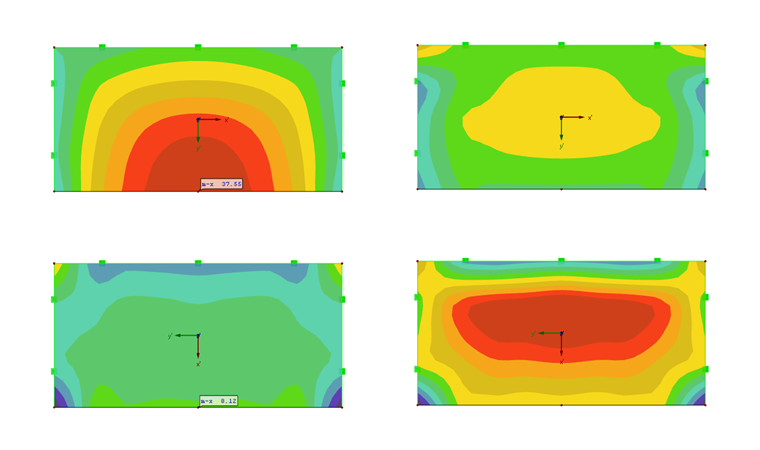
Los máximos momentos flectores resultantes de las chapas ortótropas son iguales a m_x con la rigidez en la dirección x y para m_y con la mayor rigidez en la dirección y.

Para la chapa con la mayor rigidez en la dirección y, el mayor momento flector m_y está casi en el centro de la chapa (figura 07).

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Variación de la deformación transversal

La deformación transversal según los diagramas de deformaciones puede alcanzar los valores máximos y mínimos enumerados en la tabla para un material de resistencia C24.

	Máx.	Mín.
ν_xy	5,447	-5,447
ν_yx	0,183	-0,183

Para este propósito, la chapa introducida al principio con la alta rigidez (E_x = 11 000) se va a definir con estas deformaciones transversales altas. Las otras rigideces de la chapa, sin embargo, permanecen sin cambios.

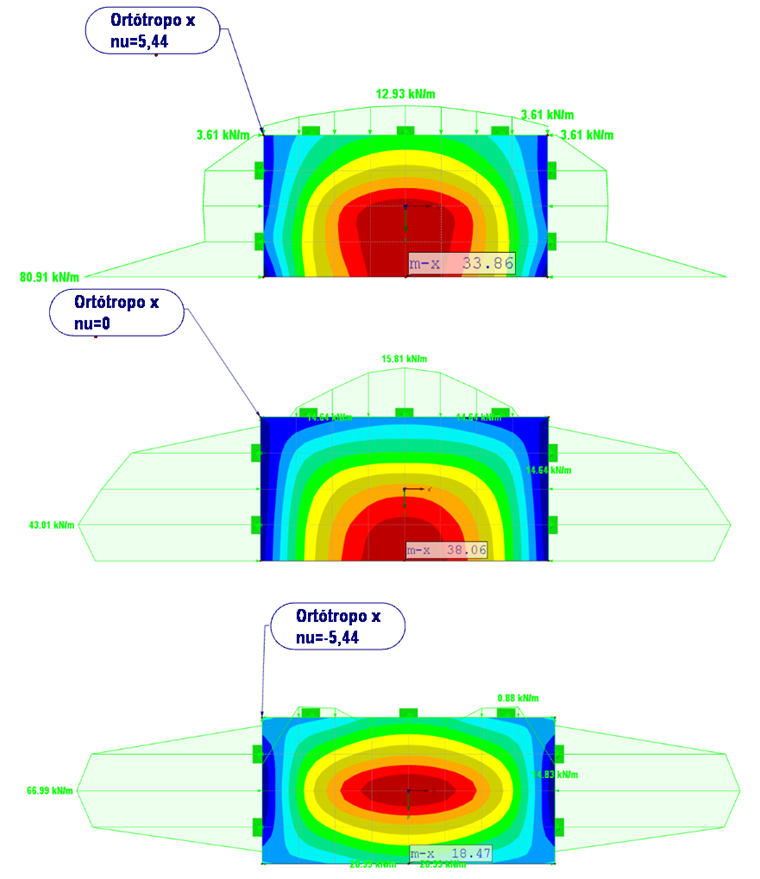
La figura 08 muestra los resultados de la variación de ν_xy = 5,44 a -5.44.

Para ν _xy = 5,44, las reacciones de los apoyos son cualitativamente idénticas al comportamiento del material isótropo. El momento flector aumenta desde m_x 0 18,1 kNm/m (chapa isótropa) a m_x = 34,9 kNm/m (chapa ortótropa).

Comparado con la chapa ortótropa con deformaciones transversales comunes (ν_xy = 2,5), el momento flector está ligeramente reducido.

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, medio: νxy = 0, Derecha: νxy = -5,44)

Con ν_xy = 0, la amplitud elevada de la reacción en el apoyo en el final libre de la chapa ha cambiado a un valor constante de 43 kN/m.

El momento m_x aumenta hasta 38,1 kNm/m. Comparado con el resultado previo (v_xy = 5,44), aquí se muestra la influencia de la deformación transversal. Para ν = 0, no se produce ninguna deformación o distorsión debido a la deformación transversal.

Para ν _xy = -5,44, se muestra una rotura postcrítica en el extremo libre de la chapa y las reacciones de soporte se vuelven negativas. El momento máximo se produce en el centro de la chapa con 59,5 kNm/m.

La placa ahora se comporta más que una placa tensada uniaxialmente, sin el tercer apoyo en la dirección longitudinal.

Este comportamiento se puede explicar con la figura 01 y la relación ahí numerada.

Debido a la deformación transversal negativa elevada (ν_xy = -5,44), la chapa está sometida completamente a una sobrepresión en el extremo libre y, por lo tanto, no se puede deformar.

Aquí, la influencia de la ortotropía en la dirección y es casi nula (E_y ≈ 0).

Conclusión

Casi cualquier parámetro del material se puede definir con el modelo de material ortótropo en RFEM. Son posibles resultados muy diferentes con la variación de las deformaciones transversales. Una deformación transversal, después de la modificación de los valores según [1], da como resultado valores próximos a la solución para una viga de vano simple.

Ecuación 31:

M_{y} = \frac{q l^{2}}{8} = 40 kNm

Fórmula 36

Las deformaciones transversales negativas demasiado altas muestran un sistema estructural modificado que ya no se corresponde con el modelado.

Autor

El Sr. Kuhn es responsable del desarrollo de productos para estructuras de madera y proporciona soporte técnico a nuestros clientes.

Enlaces

Análisis estructural no lineal

Referencias

Huber, M. T : The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

Descargas

Archivo del modelo de RFEM 1

472 KB

Archivo del modelo de RFEM 2

460 KB

;