16131x

001525

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

27.06.2018

Lois de matériau orthotrope

Les lois de matériau orthotrope sont utilisées dès lors que les matériaux sont disposés en fonction de leur chargement. Nous pouvons citer comme exemple les plastique renforcé de fibres, les tôles trapézoïdales, le béton armé et le bois.

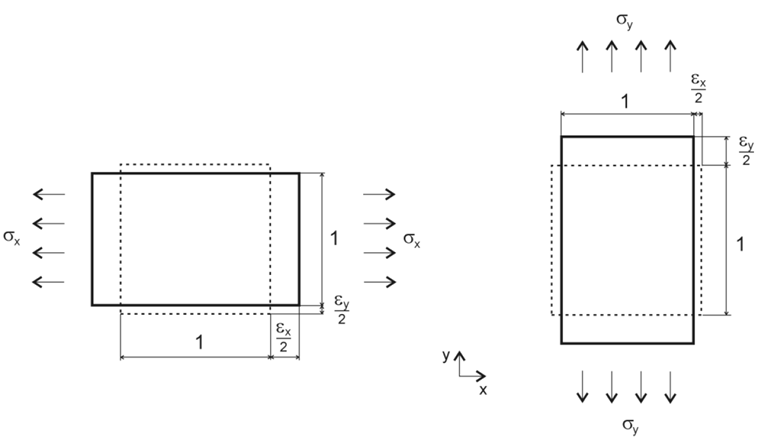
La loi de Hooke est habituellement incluse pour les matériaux orthotropes

u = \frac{E}{2 G} - 1 \leq 0.5

Formule 1

- 1 < u < 0.5

Formule 2

n'est plus valide.

Allongement transveral

Les paramètres de matériau suivants sont relatifs à des rigidités bidirectionnelles et, à moins que le contraire ne soit précisé, de matériau bois. Comme affiché dans la Figure 01, nous utilisons un système d’axe local.

E_x = rigidité dans la direction x locale de la surface
E_y = rigidité dans la direction y locale de la surface
G_xz = rigidité de cisaillement dans la direction x locale de la surface (direction d’épaisseur de la plaque)
G_yz = rigidité de cisaillement dans la direction y locale de la surface (direction d’épaisseur de la plaque)
G_xy = rigidité de cisaillement dans la zone dans le plan
ν_xy = déformation transversale dans la direction x
ν_yx = déformation transversale dans la direction y

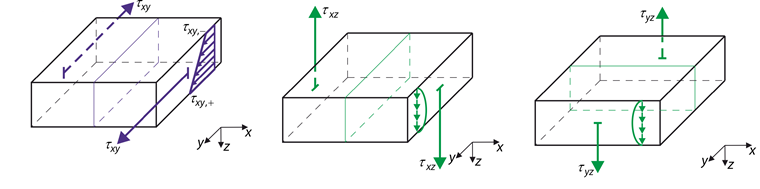
Les contraintes dans la Figure 02 sont relatives aux rigidités mentionnées ici.

contraintes de cisaillement

La loi de matériau est sujette aux règles suivantes.

Équation 1 :

\frac{u_{yx}}{E_{y}} = \frac{u_{xy}}{E_{x}}

Formule 3

Équation 2 :

u_{xy} ⩾ u_{yx}

Formule 4

Équation 3 :

u_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot u_{yx}

Formule 5

Équation 4 (rigidités dans la zone du plan):

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}] \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}]

Formule 6

Le ratio de déformations dans les équations ci-dessus souligne les relations dans la Figure 01.

Les rigidités dans la zone dans le plan sont calculées comme suit.

Équation 5 :

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix}]

Formule 7

Déformation transversale ν

Comme expliqué dans la Figure 01, les déformations etcontraintes modifiées dans cette direction résultent d’un comportement dematériau lissé dans la direction respective.

Ratio des déformations :

Équation 6 :

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

Formule 8

Équation 7 :

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

Formule 9

Question simple – réponse rapide :

σ_{x} e q 0, σ_{y} = 0, σ_{xy} = 0

Formule 10

les équations suivantes sont obtenues avec la loi de Hooke.

Équation 8 :

ε_{x} = \frac{σ_{x}}{E_{x}}

Formule 11

Équation 9:

ε_{y} = \frac{σ_{y}}{E_{y}}

Formule 12

Équation 10:

σ_{y} = ε_{y} \cdot E_{y} with E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

Formule 13

Équation 11:

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

Formule 14

Équation 12:

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} with ν_{xy} = - \frac{ε_{y}}{ε_{x}}

Formule 15

Équation 13:

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

Formule 16

Matrice de rigidité

Calcul de la matrice de rigidité globale de la plaque.

Équation 14:

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix}]

Formule 17

Composants du fléchissement:

Équation 15:

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Formule 18

Équation 16:

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

Formule 19

Équation 17:

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Formule 20

Équation 18:

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

Formule 21

Composants de membrane:

Équation 19:

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - u_{xy} u_{yx}}

Formule 22

Équation 20:

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

Formule 23

Équation 21:

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - u_{xy} u_{yx}}

Formule 24

Équation 22:

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

Formule 25

Composants du cisaillement:

Équation 23:

D_{44} = \frac{5}{6} G_{xz} \cdot d

Formule 26

Équation 24:

D_{55} = \frac{5}{6} G_{yz} \cdot d

Formule 27

La matrice de rigidité doit être définie positive pour ces équations, de sorte que toutes les valeurs propres de la matrice soient positives.

C’est pour cette raison que RFEM contrôle, entre autres, la définition de la déformation transversale relative à l’équation suivante.

Équation 25 :

u_{xy} \leq 0.999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Formule 28

Exemple

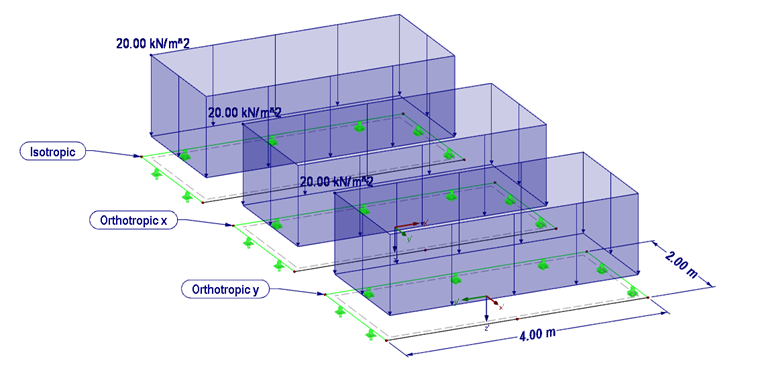
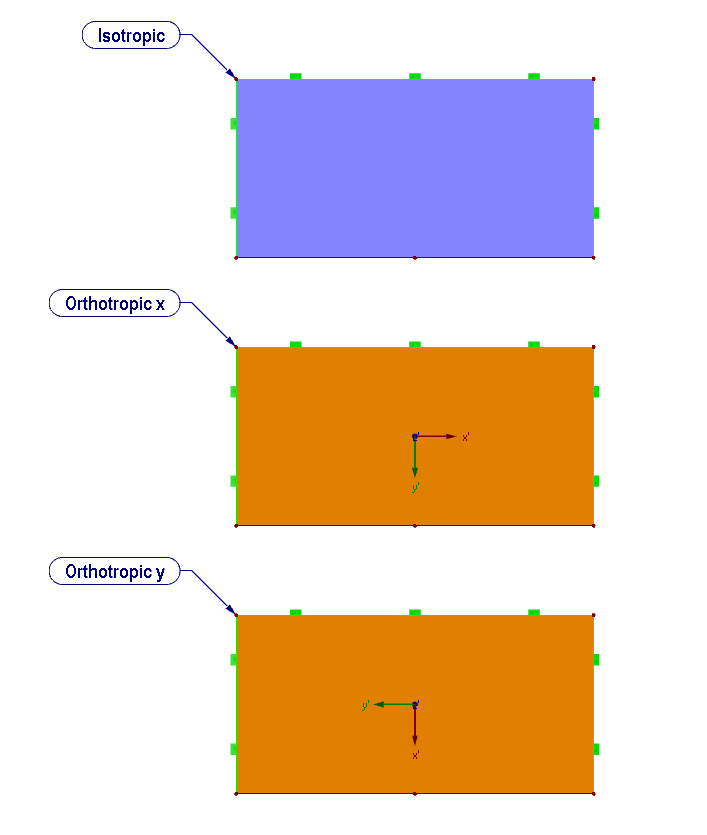
Le comportement de matériau orthotrope sera expliqué à l’aide de l’exemple suivant (Figure 03). Un matériau orthotrope sera comparé à un matériau isotrope. De plus, la rigidité d’une plaque orthotrope sera définie avec une rigidité élevée dans la direction x et y.

Système

Construction :

Épaisseur de plaque 200 mm
Matériau C 24
Rigidités orthotropes

$\begin{array}{l} E_{x} = 1, 100.0 kN / {cm}^{2} \\ E_{y} = 37.0 kN / {cm}^{2} \\ G_{y} = 6.9 kN / {cm}^{2} \\ G_{x} = 69.0 kN / {cm}^{2} \\ G_{xy} = 69.0 kN / {cm}^{2} \\ u_{xy} = 2.52 \\ u_{yx} = 0.085 \end{array}$

Formule 29
Rigidités isotropes

$\begin{array}{l} E = 1, 100 kN / {cm}^{2} \\ G = 500 kN / {cm}^{2} \\ u = 0.1 \end{array}$

Formule 30
Dimension l = 2.0 m, L = 4.0 m
Charge: 20 kN/m²
Taille du maillage EF: 50 cm

La structure est définie comme encastrée dans la direction z verticale. Les conditions d’appui dans les directions x et y ont été sélectionnées de sorte qu’aucun effet dû aux maintiens n’ait lieu.

Le calcul est réalisé selon l’analyse statique linéaire avec des conditions d’appui et un comportement de matériau linéaire élastique.

La déformation transversale suivante est un résultat de la loi de Hooke appliqué aux valeurs données.

Équation 26 :

ν = (\sqrt{E_{x} \cdot E_{y}}) / (2 G) - 1 = 6.97

Formule 31

Cette déformation transversale élevée est impossible avec le modèle sélectionné. Avec les équations de [1], les valeurs peuvent toutefois être ajustées.

Équation 27 :

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Formule 32

Équation 28 :

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

Formule 33

Équation 29 :

ν_{xy} = (\frac{\sqrt{1, 100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1, 100}{37}} = 2.52

Formule 34

Équation 30 :

ν_{xy} = (\frac{\sqrt{1, 100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1, 100}} = 0.085

Formule 35

Surfaces et rigidités

Résultats :
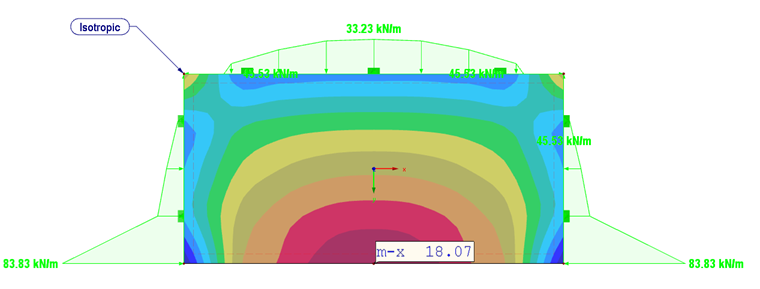
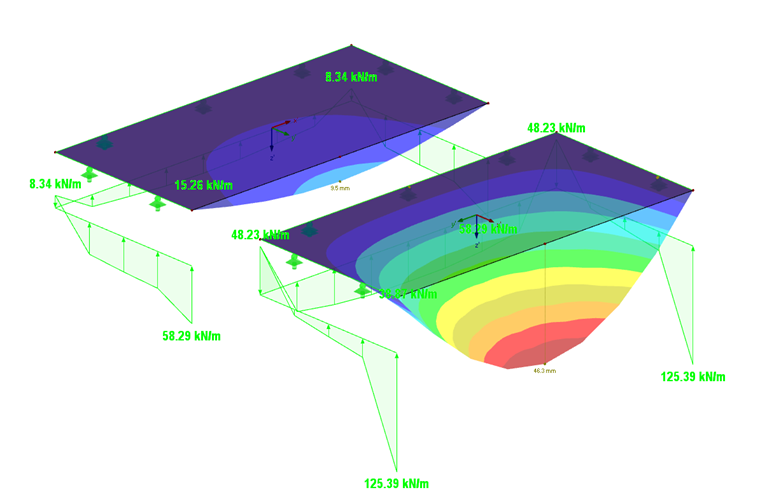
Comme prévu, les plus grandes déformations ont lieu avec l’orientation des rigidités dans la direction y (Figure 06). Les réactions d’appui et le moment de la plaque isotrope sont affichés dans la Figure 05.

Résultats de matériau isotrope

La plaque avec une rigidité importante dans la direction y (Ey = 1 100 kN/cm^{2) ayant une résistance importante dans cette direction, les réactions d’appui sont également plus élevées (125,4 kNm contre 58,3 kNm).}

Déformations et réactions d'appui des plaques orthotropes

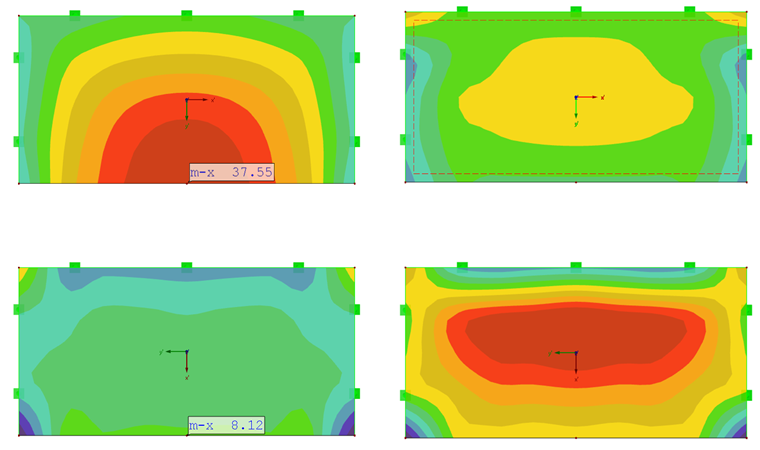
Les moments de flexion maximum résultants pour les plaques orthotropes sont égaux à m_x avec la rigidité en direction x et pour m_y avec une rigidité importante en direction y.

La plaque à la rigidité élevée dans la direction-y a son moment fléchissant m_y quasiment en son centre (Figure 07).

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Variation de la déformation transversale

La déformation transversale relative aux diagrammes de déformation peut atteindre les valeurs maximale et minimale listées dans ce tableau pour un matériau de résistance C24.

	Max.	Min.
ν_xy	5,447	-5,447
ν_yx	0,183	-0,183

La plaque à rigidité importante vue précédemment (E_x = 11,000) sera définie avec ces déformations transversales élevées. Les autres rigidités de plaque restent toutefois identiques.

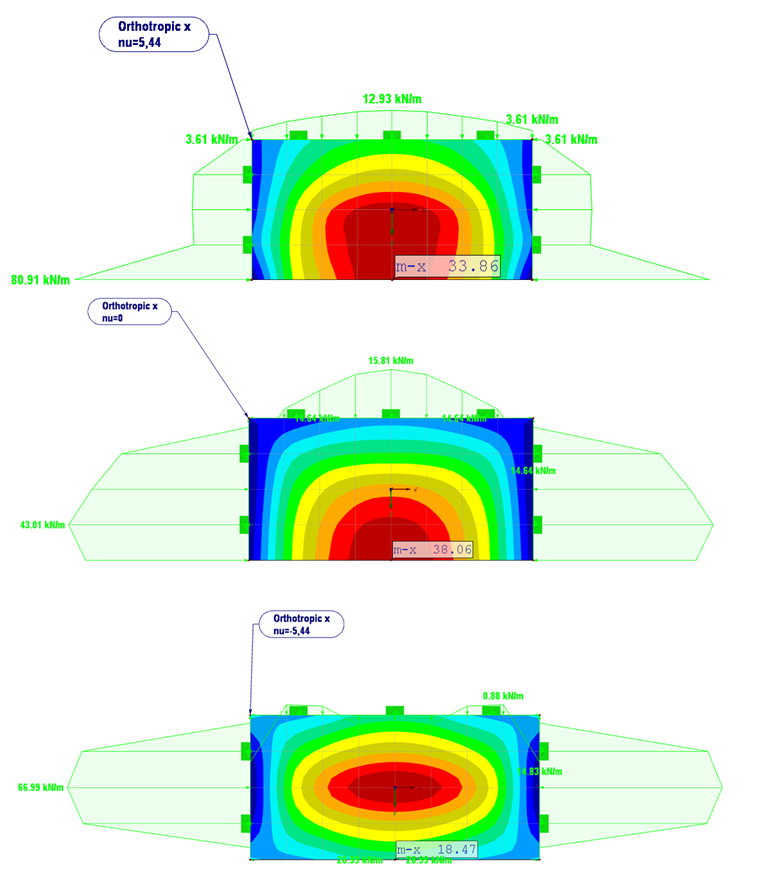
La Figure 08 affiche les résultats de la variation de ν_xy = 5,44 à -5,44.

Pour ν_xy = 5,44 les réactions d’appui sont qualitativement identiques à celles du comportement de matériau isotrope. Le moment fléchissant passe de m_x = 18.1 kNm/m (plaque isotrope) à m_x = 34.9 kNm/m (plaque orthotrope).

Le moment fléchissant est légèrement réduit en comparaison aux déformations transversales habituelles (ν_xy = 2.5).

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, Milieu: νxy = 0, à droite: νxy = -5,44)

Avec ν_xy = 0, la grande amplitude de valeurs des réactions d’appui de la fin libre de plaque est remplacée par une valeur constante de 43 kN/m.

Le moment m_x augmente à 38.1 kNm/m. Relativement au résultat précédent (ν_xy =5.44), l’influence de la déformation transversale est perceptible visuellement. Pour v = 0, aucune déformation ou distorsion n’est causée par la déformation transversale.

Pour ν_xy = -5,44 un échec post-critique est affiché en fin de plaque et les réactions d’appui deviennent alors négatives. Le moment maximum a lieu dans le centre de la plaque avec 59,5 kNm/m.

La plaque a maintenant un comportement plus proche de celui d’une plaque sous contraintes uniaxales sans troisième appui dans la direction longitudinale.

Ce comportement peut être expliqué avec la Figure 01 et la relation qui y est listée.

La déformation transversale négative élevée (ν_xy = -5,44), provoque un échec sous charge de la bordure libre et ne peut ainsi pas être déformée.

L’influence de l’orthotropie dans la direction y est ici quasi-nulle (E_y ≈ 0).

Conclusion

Presque tous les paramètres de matériau peuvent être définis avec un matériau orthotrope dans RFEM. La variation des déformations transversales permet d’obtenir des résultats très différents. Une déformation transversale suite à la modification des valeurs selon [1] résulte de valeurs proches de la solution pour une poutre à travée simple.

Équation 31:

M_{y} = \frac{q l^{2}}{8} = 40 kNm

Formule 36

Les déformations transversales négatives trop élevées affichent un système structural modifié qui ne correspond pas à la modélisation.

Auteur

M. Kuhn est responsable du développement de produits pour les structures en bois et fournit une assistance technique à nos clients.

Liens

Logiciels pour les analyses non linéaires

Références

Huber, M. T : The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

Téléchargements

;