7868x

001536

Sonja von Bloh, M.Sc.

2018-09-12

Усиленные панели с потерей устойчивости согласно EN 1993-1-5, раздел 4.5

В SHAPE-THIN можно выполнить расчет усиленных панелей с потерей устойчивости в соответствии с разделом 4.5 нормы EN 1993-1-5. Для усиленных панелей с потерей устойчивости должны учитываться эффективные поверхности от местной потери устойчивости отдельных панелей в плите и в элементах жесткости, а также эффективные поверхности от всей потери устойчивости панели.

прежде всего, эффективные поверхности отдельных панелей задаются с помощью понижающего коэффициента по EN 1993-1-5 [1] , раздел 4.4 для учета потери устойчивости отдельных панелей. На втором этапе определяется устойчивость всей панели с учетом потери устойчивости, аналогичной работе одного из стержней с потерей устойчивости. С понижающим коэффициентом общей потери устойчивости панели, расчетная ширина отдельных панелей снова уменьшается. В результате получается эффективное сечение, которое можно рассматривать как принадлежащее к классу сечений 3.

Пример

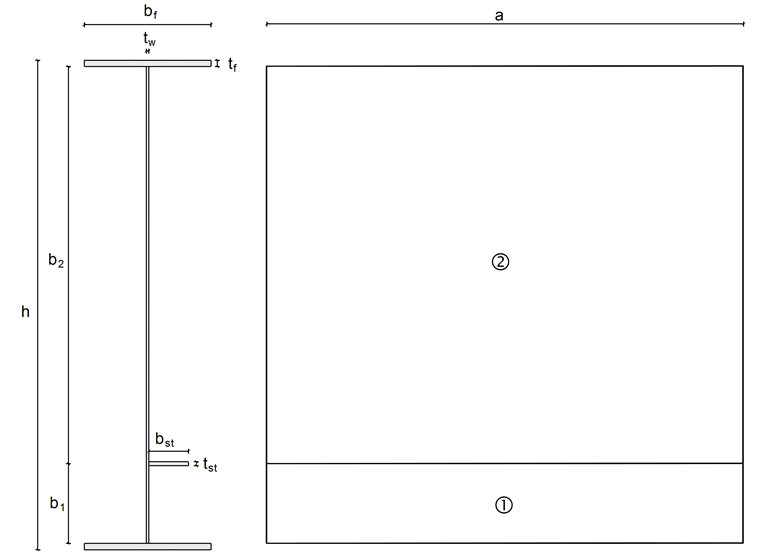
Следующий пример взят из Ежегодника строительных конструкций за 2015 год [2]. Сечение состоит из двутавровой балки, стенка которой усилена жесткими поперечными элементами жесткости и продольным элементом жесткости. Поперечные элементы жесткости расположены на расстоянии 3 000 мм друг от друга, а продольный элемент жесткости приварен на расстоянии 500 мм от нижней полки. Сварными швами пренебрегаем. Действует сжимающая нормальная сила N_Ed = 4000 кН.

Сечение

Материал:
S355 J0
f_y = 35,5 кН/см² (for t ≤ 3 мм и t ≤ 16 мм)
f_y = 34,5 кН/см² (для t >16 мм и t ≤ 40 мм)
E = 21 000 кН/см²
G = 8 076,92 кН/см²
γ_M0 = 1,0

a = 3 000 мм
b₁ = 500 мм
b₂ = 2 500 мм
b_f = 800 мм
b_st = 250 мм
t_w = 15 мм
t_f = 40 мм
t_st = 25 мм
h = 3 080 мм

Сечение брутто и распределение напряжений

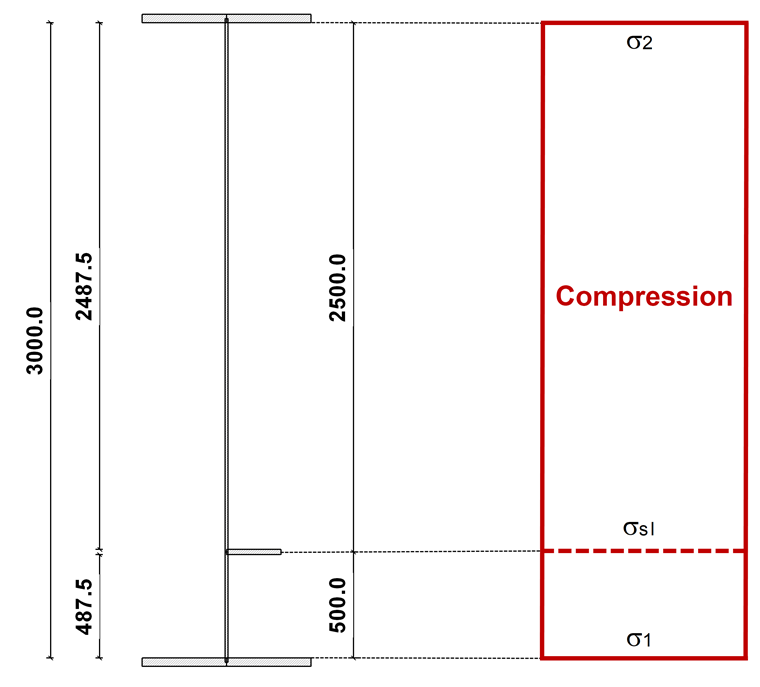
Напряжение рассчитывается следующим образом:

σ_{1} = σ_{sl} = σ_{2} = \frac{N_{Ed}}{A} = \frac{4.000}{1.152, 5} = 3, 47 kN / cm ²

Формула 1

Сечение брутто и распределение напряжений показаны на Рисунке 02.

распределение напряжений

Классификация сечений

В ходе классификации сечения выполняется оценка, чтобы определить, необходим ли для отдельных панелей расчет на потерю устойчивости. Если отдельная панель имеет сечение хотя бы класса 3, то местная деформация не будет определяющей.

Полка

\begin{array}{l} c_{f} = \frac{b_{f} - t_{w}}{2} = \frac{800 - 15}{2} = 392, 5 mm \\ \frac{c_{f}}{t_{f}} = \frac{392, 5}{40} = 9, 8 \end{array}

Формула 2

Максимальное отношение c/t λ_i определяется в соответствии с EN 1993-1-1 [3] , таблица 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{c_{f}}{t_{f}} = 9, 8 \end{array}

Формула 3

Полка должна быть придана к сечению класса 3. Таким образом, местная потеря устойчивости не будет определяющей, и не требуется уменьшения отдельных панелей полки.

Стенка

\begin{array}{l} c_{1} = b_{1} - \frac{t_{st}}{2} = 500 - \frac{25}{2} = 487, 5 mm \\ \frac{c_{1}}{t_{w}} = \frac{487, 5}{15} = 32, 5 \end{array}

Формула 4

Максимальное отношение c/t λ_i определяется согласно [3] , таблица 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 > \frac{c_{1}}{t_{w}} = 32, 5 \end{array}

Формула 5

Отдельная панель 1 должна быть придана к сечению класса 3. Таким образом, местная потеря устойчивости не будет определяющей, и не требуется уменьшения отдельных панелей полки.

\begin{array}{l} c_{2} = b_{2} - \frac{t_{st}}{2} = 2.500 - \frac{25}{2} = 2.487, 5 mm \\ \frac{c_{2}}{t_{w}} = \frac{2.487, 5}{15} = 165, 8 \end{array}

Формула 6

Максимальное отношение c/t λ_i определяется согласно [3] , таблица 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 < \frac{c_{2}}{t_{w}} = 165, 8 \end{array}

Формула 7

Отдельная панель 2 должна быть придана к сечению класса 4. Таким образом, местная потеря устойчивости является определяющей для данной панели и необходимо ее уменьшить.

Жесткость

\begin{array}{l} b_{st} = 250 mm \\ \frac{b_{st}}{t_{st}} = \frac{250}{25} = 10 \end{array}

Формула 8

Максимальное отношение c/t λ_i определяется согласно [3] , таблица 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{b_{st}}{t_{st}} = 10 \end{array}

Формула 9

Стенка должна быть придана к сечению класса 3. Таким образом, местная потеря устойчивости не будет определяющей, и не требуется уменьшения этой отдельной панели.

Расчётная ширина

Отдельная панель 1 придана к сечению класса 3, поэтому местная потеря устойчивости не будет определяющей. Эффективные значения сечения соответствуют значениям сечения брутто. Согласно [1] , таблица 4.1, мы получим следующие полезные ширины:

\begin{array}{l} b_{1, eff} = c_{1} = 487, 5 mm \\ b_{1, edge, eff} = b_{1, edge} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \\ b_{1, \inf, eff} = b_{1, \inf} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \end{array}

Формула 10

Отдельная панель 2 придана к сечению класса 4, поэтому местная потеря устойчивости не будет определяющей. Расчетные ширины отдельной панели 2 должны определяться по [1] , раздел 4.4.

Распределение напряжений в отдельной панели 2 - равномерное. Это приводит к коэффициенту напряжений ψ = 1 и, согласно таблице 4.1, к величине потери устойчивости k_σ = 4,0. Результат для коэффициента гибкости λ_p2 согласно [1] , раздел 4.4(2), равен:

${\bar{λ}}_{p 2} = \frac{\frac{c_{2}}{t_{w}}}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{165, 8}{28, 4 \cdot 0, 814 \cdot \sqrt{4}} = 3, 588$ Формула 12	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Формула 13
	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Формула 14

Местный понижающий коэффициент ρ определяется согласно [1] , формула (4.2):

ρ_{2} = \frac{{\bar{λ}}_{p 2} - 0, 055 \cdot (3 ψ)}{{\bar{λ}}_{p 2}^{2}} = \frac{3, 588 - 0, 055 \cdot (3 1)}{3, 588^{2}} = 0, 262 < 1

Формула 15

Полезные ширины отдельной панели 2, с учетом местной потери устойчивости, рассчитываются согласно [1] , таблица 4.1:

\begin{array}{l} b_{2, eff} = ρ_{2} \cdot c_{2} = 0, 262 \cdot 2.487, 5 = 650, 7 mm \\ b_{2, edge, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \\ b_{2, \sup, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \end{array}

Формула 16

Ширины сечения брутто получаются:

\begin{array}{l} b_{2, edge} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \\ b_{2, \sup} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \end{array}

Формула 17

Работа как плита

Упругое критическое напряжение потери устойчивости элемента жесткости σcr,sl рассчитывается согласно [1] , Приложение A.2.2. Сначала должна быть вычислена расчетная длина элемента жесткости a_c :

a_{c} = 4, 33 \cdot \sqrt[4]{\frac{I_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}}{t^{3} \cdot b}} = 4, 33 \cdot \sqrt[4]{\frac{11.900 \cdot 50^{2} \cdot 250^{2}}{1, 5^{3} \cdot (50 250)}} = 896, 4 cm > a = 300 cm

Формула 18

Упругое критическое напряжение потери устойчивости элемента жесткости σ_{cr,sl равно} a < a_c в:

\begin{array}{l} σ_{cr, sl} = \frac{π^{2} \cdot E \cdot I_{sl, 1}}{A_{sl, 1} \cdot a^{2}} + \frac{E \cdot t^{3} \cdot b \cdot a^{2}}{4 \cdot π^{2} \cdot (1 - ν^{2}) \cdot A_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}} für a < a_{c} \\ σ_{cr, sl} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} + \frac{21.000 \cdot 1, 5^{3} \cdot (50 250) \cdot 300^{2}}{4 \cdot π^{2} \cdot (1 - 0, 3^{2}) \cdot 289, 4 \cdot 50^{2} \cdot 250^{2}} = 95, 9 kN / {cm}^{2} \end{array}

Формула 19

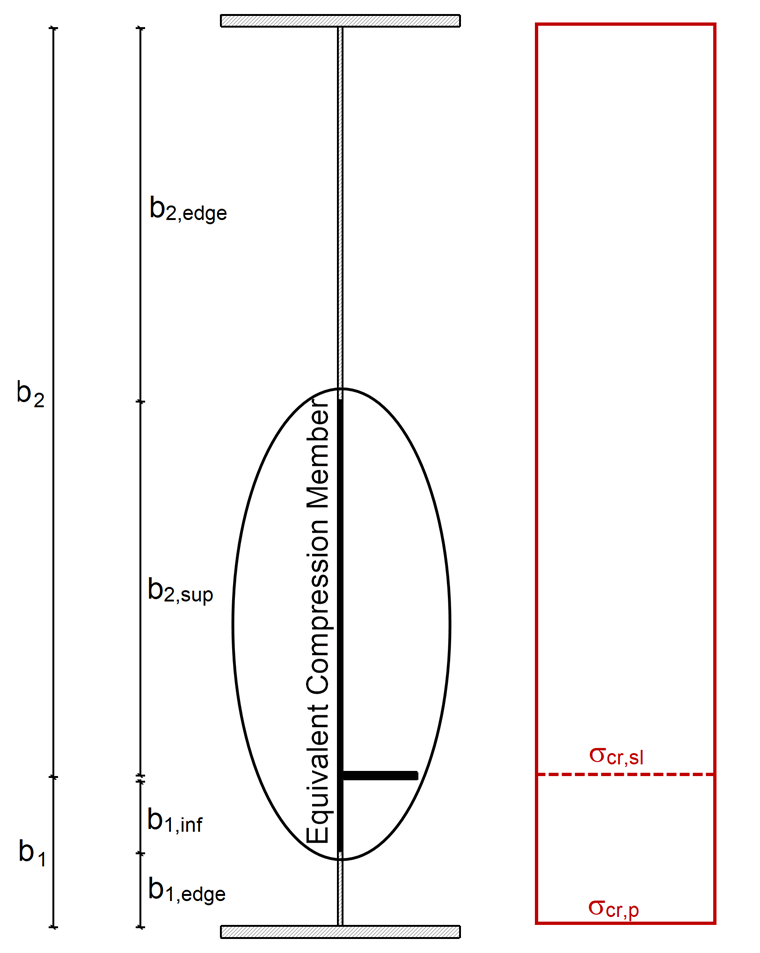
I_sl,1 и A_sl,1 здесь представляют момент инерции площади сечения брутто и площадь сечения брутто эквивалентного сжатого элемента согласно [1] ; A.2.1(2) для потери устойчивости перпендикулярно плоскости плиты, а также b₁ и b₂ описывают расстояния от элементов жесткости до продольных краев (b₁ + b₂ = b).

Распределение напряжений - равномерное. Следовательно, упругое напряжение потери устойчивости плиты σ_cr,p соответствует критическому напряжению потери устойчивости σ_cr,sl.

σ_{cr, p} = σ_{cr, sl} = 95, 9 kN / {cm}^{2}

Формула 20

Эквивалентный сжатый стержень сечения брутто

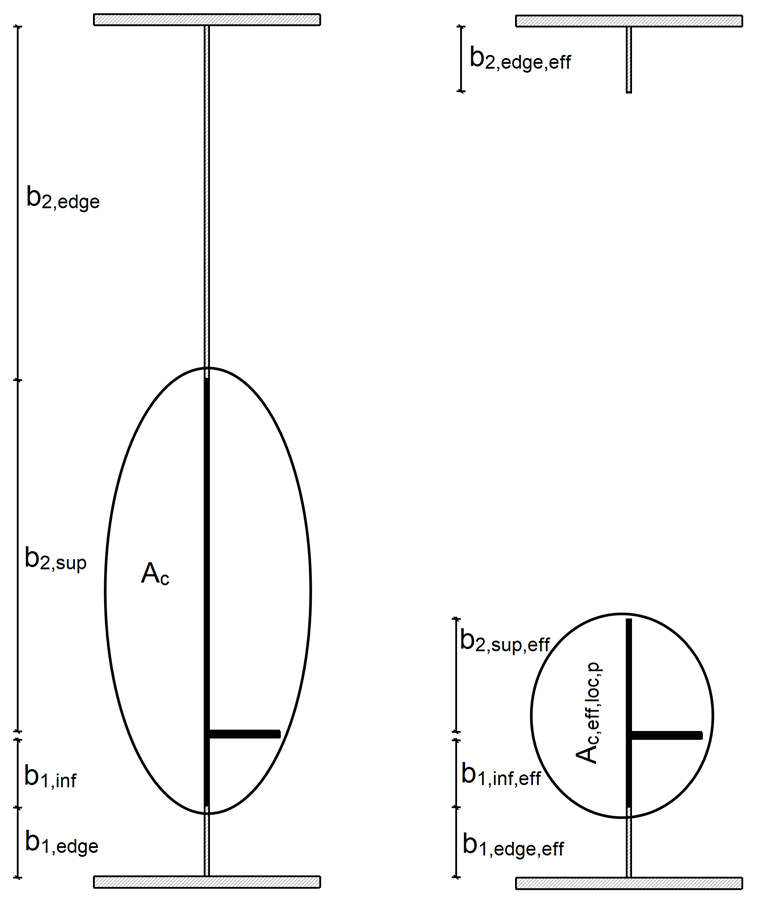
Площадь сечения брутто A_c панели плиты с продольными элементами жесткости рассчитывается следующим образом, без учета крайних плит, опертых на смежные компоненты плиты, и полезной площади сечения A_c,eff,loc,p площади описанных выше:

A_{c} = (b_{1, \inf} + b_{2, \sup} + t_{st}) \cdot t_{w} + b_{st} \cdot t_{st} = (24, 38 + 124, 38 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 289, 4 {cm}^{2}

Формула 21

Жесткость относится к сечению класса 3, поэтому полезная площадь сечения жесткости соответствует площади сечения брутто жесткости.

A_{c, eff, loc, p} = (b_{1, \inf, eff} + b_{2, \sup, eff} + t_{st}) \cdot t_{w} + b_{st, eff} \cdot t_{st} = (24, 38 + 32, 54 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 151, 6 {cm}^{2}

Формула 22

Характеристики сечения показаны на Рисунке 04.

Сечение брутто и эффективное сечение при местной потере устойчивости

Понижающий коэффициент β_a,c,p рассчитан согласно [1] , раздел 4.5.2, следующим образом:

\begin{array}{l} β_{a, c, p} = \frac{A_{c, eff, loc, p}}{A_{c}} \\ β_{a, c, p} = \frac{151, 6}{289, 4} = 0, 524 \end{array}

Формула 23

Общая гибкость λ_p усиленной плиты согласно [1] , формула (4.7), равна:

${\bar{λ}}_{p} = \sqrt{\frac{β_{a, c, p} \cdot f_{y}}{σ_{cr, p}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{95, 9}} = 0, 440$ Формула 25	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Формула 26
	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Формула 27

Согласно [1] , 4.4 (2), коэффициент гибкости λ_p меньше предельного значения 0,673. Таким образом, не требуется уменьшения из-за работы плиты; например, ρ_p = 1,0.

Работа плиты при потере устойчивости

Упругое критическое напряжение потери устойчивости σ_cr,c определяется согласно [1] , раздел 4.5.3(3). Прежде всего, напряжение потери устойчивости σ_cr,c,sl элемента жесткости, расположенного на сжатом крае с максимальной нагрузкой, определяется по [1] , формула (4.9).

σ_{cr, c, sl} = \frac{π^{2} \cdot E \cdot I_{sl}}{A_{sl} \cdot a^{2}} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} = 94, 7 kN / {cm}^{2}

Формула 28

Распределение напряжений - равномерное. Поэтому упругое критическое напряжение потери устойчивости σ_cr,c соответствует упругому напряжению потери устойчивости σ_cr,c,sl элемента жесткости, который расположен на сжатом крае с максимальной нагрузкой.

σ_cr,c = σ_cr,c,sl = 94,7 кН/см²

Понижающий коэффициент β_a,c,c рассчитывается согласно [1] , раздел 4.5.3(4) следующим образом:

β_{a, c, c} = \frac{A_{sl, eff}}{A_{sl}} = \frac{151, 6}{289, 4} = 0, 524

Формула 29

Коэффициент гибкости λcрезультатов эквивалентных сжатых стержней, согласно [1] , уравнение (4.11), в:

{\bar{λ}}_{c} = \sqrt{\frac{β_{a, c, c} \cdot f_{y}}{σ_{cr, c}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{94, 7}} = 0, 443

Формула 31

Согласно [1] , раздел 4.5.3(5), радиус вращения i рассчитывается следующим образом:

i = \sqrt{\frac{I_{sl}}{A_{sl}}} = \sqrt{\frac{11.900}{289, 4}} = 6, 41 cm

Формула 32

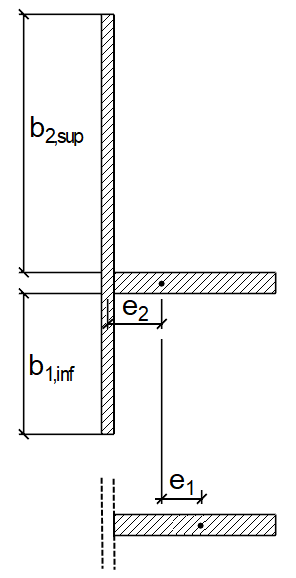
Расстояние e является большим из двух расстояний согласно [1] , рисунок A.1; например, либо расстояние e₁ отдельного элемента жесткости, установленное между центром тяжести и учитываемое независимо от плиты, без расчетной ширины, до центральной оси усиленной плиты, либо расстояние e₂ от центральной оси усиленной плиты панель к средней плоскости плиты. Расстояния показаны на Рисунке 05.

Эквивалентный сжатый стержень и элемент жесткости: Расстояния e1, e2

e = max (e₁, e₂ ) = max (10,39 см, 2,86 см) = 10,39 см

Коэффициент несовершенства αe определяется согласно [1] , формула (4.12) с α = 0,49, для открытых усиленных сечений следующим образом:

α_{e} = α \frac{0, 09}{i / e} = 0, 49 \frac{0, 09}{6, 41 / 10, 39} = 0, 636

Формула 33

Понижающий коэффициент χ_c определяется согласно [3] , 6.3.1.2:

\begin{array}{l} ϕ = 0, 5 \cdot (1, 0 α_{e} \cdot ({\bar{λ}}_{c} - 0, 2) {\bar{λ}}_{c}^{2}) = 0, 5 \cdot (1, 0 0, 636 \cdot (0, 443 - 0, 2) 0, 443^{2}) = 0, 675 \\ χ_{c} = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}_{c}^{2}}} = \frac{1}{0, 675 \sqrt{0, 675^{2} - 0, 443^{2}}} = 0, 844 < 1 \end{array}

Формула 34

Взаимодействие потери устойчивости и работы плиты

Работа конструкции всей панели определяется с коэффициентом ξ, согласно [1] , раздел 4.5.4(1):

\begin{array}{l} ξ = \frac{σ_{cr, p}}{σ_{cr, c}} - 1 jedoch 0 \leq ξ \leq 1 \\ ξ = \frac{95, 9}{94, 7} - 1 = 0, 013 \end{array}

Формула 35

Окончательный понижающий коэффициент ρc определяется по уравнению взаимодействия согласно [1] , формула (4.13):

ρ_{c} = (ρ_{p} - χ_{c}) \cdot ξ \cdot (2 - ξ) + χ_{c} = (1 - 0, 844) \cdot 0, 013 \cdot (2 - 0, 013) + 0, 844 = 0, 848

Формула 36

Характеристики полезного сечения

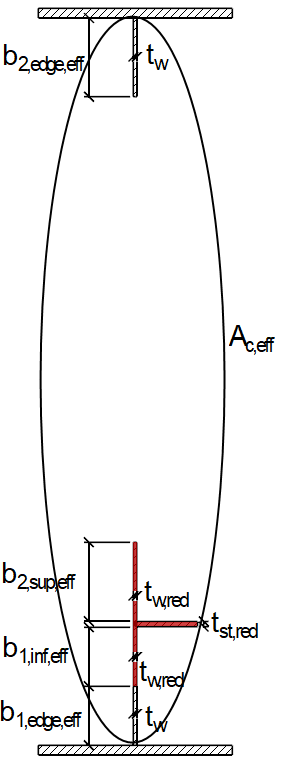
Эффективная поверхность зоны сжатия A_c,eff панели усиленной плиты рассчитывается согласно [1] , формула (4.5):

A_{c, eff} = ρ_{c} \cdot A_{c, eff, loc, p} + \sum b_{edge, eff} \cdot t = 0, 848 \cdot 151, 6 24, 38 \cdot 1, 5 + 32, 54 \cdot 1, 5 = 214, 1 cm ²

Формула 37

Полезная плоюадь сечения A_eff получается:

A_{eff} = A_{c, eff} + 2 \cdot b_{f} \cdot t_{f} = 214, 1 + 2 \cdot 80 \cdot 4 = 854, 1 cm ²

Формула 38

Эффективное сечение при местной и общей потере устойчивости

Расчет усиленной панели

Центральные оси сечения брутто и эффективного сечения не совпадают, поэтому дополнительно действующие изгибающие моменты от перемещения центральных осей эффективного сечения, связанные с центральными осями сечения брутто должны быть учтены. Дополнительные изгибающие моменты рассчитываются следующим образом:

\begin{array}{l} e_{y} = 0, 82 - 0, 72 = 0, 10 cm \\ e_{z} = 164, 97 - 157, 42 = 7, 55 cm \\ M_{y} = N \cdot e_{z} = 4.000 \cdot 7, 55 = 30.202, 4 kNcm \\ M_{z} = N \cdot e_{y} = - 4.000 \cdot 0, 10 = - 414, 3 kNcm \\ M_{u} = 30.203, 7 KNcm \\ M_{v} = - 306, 4 KNcm \end{array}

Формула 39

Максимальное напряжение получается:

σ_{eff} = \frac{N}{A_{eff}} + \frac{M_{u} \cdot e_{v}}{I_{u, eff}} - \frac{M_{v} \cdot e_{u}}{I_{v, eff}} = \frac{4.000}{854, 1} + \frac{30.203, 7 \cdot 165, 12}{17.466.764} - \frac{- 306, 4 \cdot 40, 23}{352.626} = 5, 01 kN / cm ²

Формула 40

Расчет выполняется согласно [1] , формула (4.15) следующим образом:

η_{1} = \frac{σ_{eff}}{\frac{f_{y}}{γ_{M 0}}} = \frac{5, 01}{\frac{34, 5}{1, 0}} = 0, 15

Формула 41

Расчет на потерю устойчивости при кручении

Согласно [1] , раздел 9.2.1(8) в общем случае должен выполняться следующий критерий, чтобы избежать потерю устойчивости при кручении элементов ьесткости с открытыми сечениями:

\begin{array}{l} η_{1} = \frac{5, 3 \cdot f_{y} \cdot I_{p}}{E \cdot I_{S t . V e n}} \leq 1 \\ η_{1} = \frac{5, 3 \cdot 34, 5 \cdot 13.053}{21.000 \cdot 122} = 0, 93 \leq 1 \end{array}

Формула 42

I_p и I_St.Ven описывают полярный момент инерции и момент инерции Сен-Венана одного сечения элемента жесткости (без плиты), рассчитанного вокруг точки соединения к плите.

Если учитывать жесткость депланации, сначала необходимо определить критическое напряжение потери устойчивости при кручении σ_cr. Он рассчитывается согласно [4] , уравнение (2.119) и уравнение (2.120) следующим образом:

\begin{array}{l} σ_{cr 1} = \frac{1}{I_{p}} \cdot (\frac{π^{2} \cdot E \cdot I_{ω}}{l^{2}} + G \cdot I_{St . Ven}) für l < L_{cr} \\ σ_{cr 2} = \frac{1}{I_{p}} \cdot (2 \cdot \sqrt{C_{θ} \cdot E \cdot I_{ω}} + G \cdot I_{St . Ven}) für l > L_{cr} \end{array}

Формула 43

Жесткость имеет константу депланации I_ω = 0 см⁶. Критическое напряжение потери устойчивости при кручении σ_cr упрощается до:

\begin{array}{l} σ_{cr 1} = σ_{cr 2} = \frac{1}{I_{p}} \cdot G \cdot I_{S t . V e n} \\ σ_{cr 1} = σ_{cr 2} = \frac{1}{13.053} \cdot 8.077 \cdot 122 = 75, 5 kN / cm ² \end{array}

Формула 44

Согласно [1] , раздел 9.2.1(9), критерий по 9.2.1(8) или следующий критерий должен быть в целом рассмотрен с учетом жесткости депланации:

\begin{array}{l} η_{2} = \frac{θ \cdot f_{y}}{σ_{cr 1}} \leq 1 \\ η_{3} = \frac{θ \cdot f_{y}}{σ_{cr 2}} \leq 1 \end{array}

Формула 45

При коэффициенте для обеспечения упругой работы в соответствии с классом сечения 3 согласно [5] при θ = 2 f для элементов жесткости с низкой жесткостью депланации (например, полоса или полособульбовый профиль) мы получим:

η_{2} = η_{3} = \frac{2 \cdot 34, 5}{75, 5} = 0, 91 \leq 1

Формула 46

Таким образом, расчет на потерю устойчивости при кручении выполнен.

SHAPE-THIN

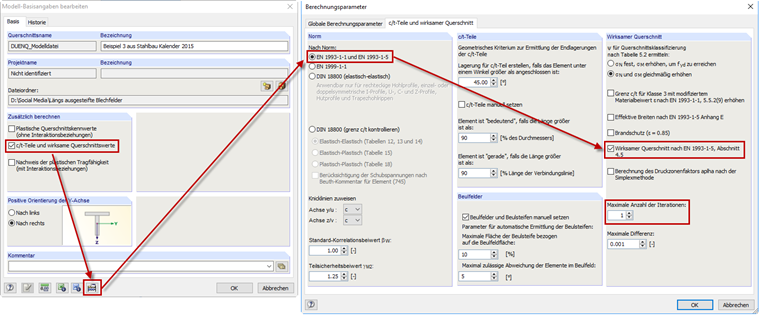
В SHAPE-THIN расчет усиленных панелей с потерей устойчивости можно выполнить в соответствии с [1] , раздел 4.5. В общих данных должна быть активирована панель управления «части c/t и эффективные характеристики сечения». После этого в параметрах расчета должны быть выбраны «EN 1993-1-1 и EN 1993-1-5» ; необходимо также выбрать панель управления «Эффективное сечение согласно норме EN 1993-1-5, раздел 4.5». Определение полезной ширины должно выполняться в процессе итерации согласно [1] , раздел 4.4(3). В нашем примере для расчета была применена только одна итерация, поэтому в программе SHAPE-THIN отразится только одна итерация (см.Рисунок 07).

Параметры расчета

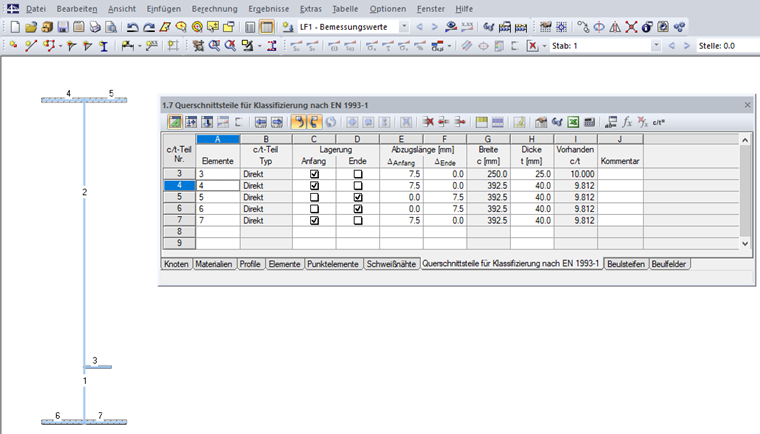
Сначала необходимо задать элементы сечения. Части c/t обычно создаются автоматически на основе геометрических условий; однако их можно создать как пользовательские в таблице «1.7 Части сечения для классификации по EN 1993-1» (см. рисунок 08) или в соответствующем диалоговом окне.

Части сечения для классификации

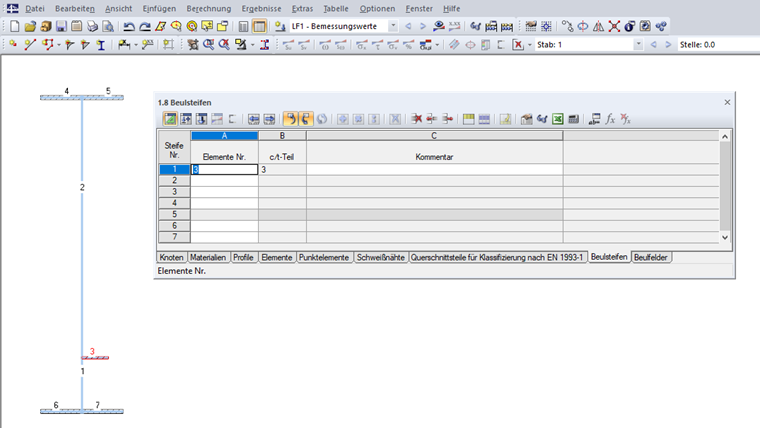
Элементы жесткости затем можно задать в таблице «1.8 Элементы жесткости» или в соответствующем диалоговом окне (см. Рисунок 09).

элементы жесткости

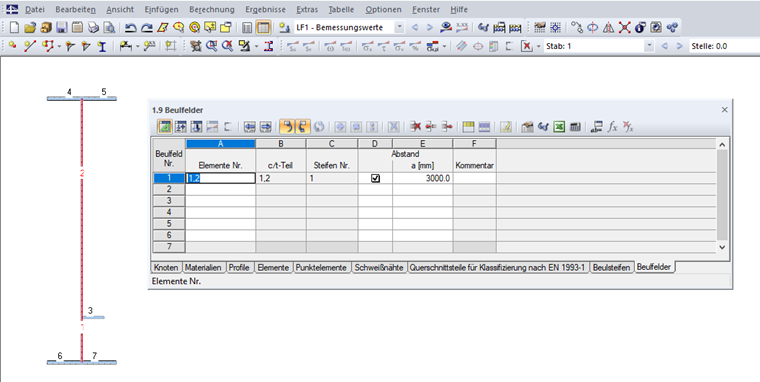
Кроме того, усиленная панель должна быть указана в таблице «1.9 Усиленные панели» (см. Рисунок 10) или соответствующем диалоговом окне. Должны быть выбраны элементы усиленной панели и необходимо задать расстояние до поперечного элемента жесткости. Если расстояние между поперечными элементами жёсткости не задано, то в расчете применяется значение a = 10 000 мм. Элементы жесткости, расположенные в усиленной панели, определяются автоматически. Усиленная панель должна опираться в начале и в конце, что означает, что здесь необходима опора.

Панели с потерей устойчивости

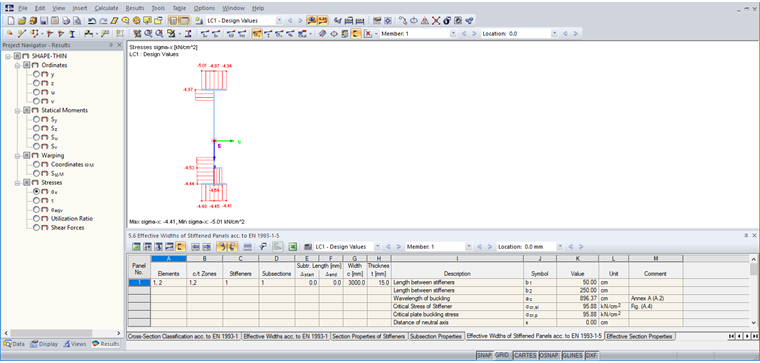
Результаты эффективного сечения можно просмотреть с помощью кнопки «Расчетная ширина».

Ergebnisse

Автор

Г-жа фон Бло оказывает техническую поддержку нашим клиентам и отвечает за разработку программы SHAPE‑THIN, а также стальных и алюминиевых конструкций.

Ссылки

Программы для расчета стальных конструкций

Ссылки

Еврокод 3: Расчет стальных конструкций - Часть 1-5: Элементы конструкции с покрытием. Издательский дом Beuth GmbH,
Beg, D .; Kuhlmann, U .; Davaine, L .; & Braun, B (2011). Расчет плоских конструкций. Еврокод 3: Расчет стальных конструкций. Часть 1-5 Расчет плоских конструкций. Берлин: Ernst & Sohn, 2013
Kuhlmann, U .: (2015). Stahlbau-Kalender 2015 – Еврокод 3 – Grundnorm, Leichtbau. Берлин: Ernst & Sohn, 2013
Йоханссон, B .; Maquoi, R .; Sedlacek, G .; Müller, C .; & Beg, D Commentary and Worked Examples to EN 1993-1-5, Plated Structural Elements. Luxemburg: Office for Official Publications of the European Communities, 2007
Еврокод 3: Расчет стальных конструкций - Часть 1‑1: Общие правила и правила для зданий. (2010). Берлин: Beuth VerLAG GmbH

Скачивания

Файл модели SHAPE-THIN

308 KB

;