7473x

12.09.2018

Panneaux avec raidisseurs longitudinaux selon EN 1993-1-5, section 4.5

Dans SHAPE-THIN, le calcul des panneaux raidis au flambement peut être effectué selon la section 4.5 de l’EN 1993-1-5. Pour les panneaux avec raidisseurs longitudinaux, les aires efficaces résultant du flambement local des différents panneaux entre les raidisseurs et les aires efficaces du flambement global du panneau raidi doivent être considérés.

L’aire efficace de chaque panneau est d'abord déterminée à l’aide d’un facteur de réduction selon l'EN 1993-1-5, 4.4 [1] afin de tenir compte du flambement local. Dans la deuxième étape, la résistance au flambement de l'ensemble de la plaque est déterminée en considérant un comportement au flambement similaire à celui des barres de flambement. Les largeurs efficaces des différents panneaux sont réduites à nouveau à l’aide du facteur de réduction pour le flambement d’ensemble du panneau. La section efficace obtenue est ainsi traitée comme appartenant à la classe de section 3.

Exemple

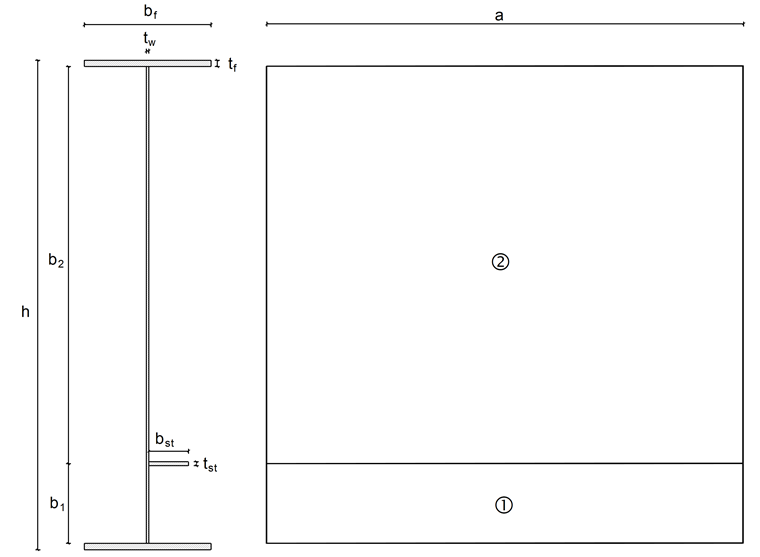
L’exemple suivant est tiré du Stahlbau-Kalender 2015 [2]. La poutre a une section en I dont l’âme est raidie par des raidisseurs transversaux et un raidisseur longitudinal. Les raidisseurs transversaux sont disposés à une espacement de 3 000 mm les uns des autres et le raidisseur longitudinal est soudé à une distance de 500 mm de la semelle inférieure. Les cordons de soudure ne sont pas pris en compte. Un effort normal en compression de N_Ed = 4 000 kN agit.

Section

Matériau :
S355 J0
f_y = 35,5 kN/cm² (pour t ≤ 3 mm et t ≤ 16 mm)
f_y = 34,5 kN/cm² (pour t >16 mm et t ≤ 40 mm)
E = 21 000 kN/cm²
G = 8 076,92 kN/cm²
γ_M0 = 1,0

a = 3 000 mm
b₁ = 500 mm
b₂ = 2 500 mm
b_f = 800 mm
b_st = 250 mm
t_w = 15 mm
t_f = 40 mm
t_st = 25 mm
h = 3 080 mm

Section brute et distribution des contraintes

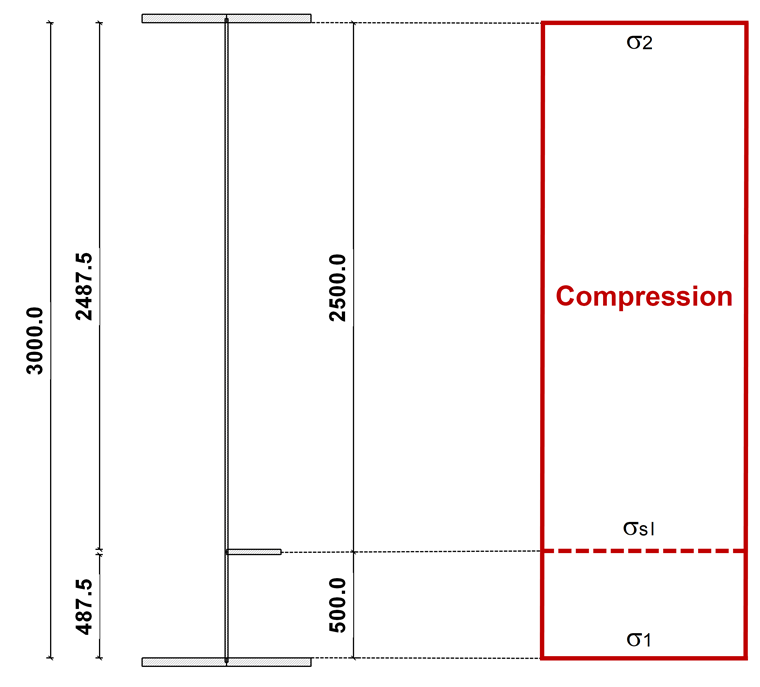
Les contraintes sont calculées comme suit :

σ_{1} = σ_{sl} = σ_{2} = \frac{N_{Ed}}{A} = \frac{4.000}{1.152, 5} = 3, 47 kN / cm ²

Formule 1

La section brute et la répartition des contraintes sont indiquées sur la Figure 02.

Distribution des contraintes

Classification des sections

Lors de la classification d'une section, une évaluation est effectuée pour déterminer si une analyse du flambement des panneaux est nécessaire. Si un panneau a une classe de section 3 au moins, le flambement local ne s'applique pas.

Semelle

\begin{array}{l} c_{f} = \frac{b_{f} - t_{w}}{2} = \frac{800 - 15}{2} = 392, 5 mm \\ \frac{c_{f}}{t_{f}} = \frac{392, 5}{40} = 9, 8 \end{array}

Formule 2

Le ratio c/t maximal λ_i est déterminé selon le Tableau 5.2 de l'EN 1993-1-1 [3].

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{c_{f}}{t_{f}} = 9, 8 \end{array}

Formule 3

La semelle doit être assignée à la classe de section 3. Ainsi, le flambement local n'est pas déterminant et il n'est pas nécessaire de réduire les panneaux de la semelle.

Âme

\begin{array}{l} c_{1} = b_{1} - \frac{t_{st}}{2} = 500 - \frac{25}{2} = 487, 5 mm \\ \frac{c_{1}}{t_{w}} = \frac{487, 5}{15} = 32, 5 \end{array}

Formule 4

Le ratio c/t maximal λ_i est déterminé selon le Tableau 5.2 de [3].

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{1}}{t_{w}} = 32.5 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 > \frac{c_{1}}{t_{w}} = 32, 5 \end{array}

Formule 5

Le panneau 1 doit être assignée à la classe de section 3. Ainsi, le flambement local ne s'exerce pas et il n'est pas nécessaire de réduire les panneaux.

\begin{array}{l} c_{2} = b_{2} - \frac{t_{st}}{2} = 2500 - \frac{25}{2} = 2487, 5 mm \\ \frac{c_{2}}{t_{w}} = \frac{2487, 5}{15} = 165, 8 \end{array}

Formule 6

Le ratio c/t maximal λ_i est déterminé selon le Tableau 5.2 de [3].

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 < \frac{c_{2}}{t_{w}} = 165, 8 \end{array}

Formule 7

Le panneau 2 doit être assignée à la classe de section 4. Le flambement local est donc déterminant pour ce panneau et une réduction du panneau est nécessaire.

Raidisseur

\begin{array}{l} b_{st} = 250 mm \\ \frac{b_{st}}{t_{st}} = \frac{250}{25} = 10 \end{array}

Formule 8

Le ratio c/t maximal λ_i est déterminé selon le Tableau 5.2 de [3].

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0.825 = 11, 6 > \frac{b_{st}}{t_{st}} = 10 \end{array}

Formule 9

L’âme doit être assignée à la classe de section 3. Ainsi, le flambement local n’est pas déterminant et il n’est pas nécessaire de réduire ce panneau.

Largeurs efficaces

Le panneau 1 est assignée à la classe de section 3, le flambement local n’est donc pas déterminant. Les valeurs de la section efficace correspondent à celle de la section brute. Selon le Tableau 4.1 de [1], il en résulte les largeurs efficaces suivantes :

\begin{array}{l} b_{1, eff} = c_{1} = 487, 5 mm \\ b_{1, edge, eff} = b_{1, edge} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \\ b_{1, \inf, eff} = b_{1, \inf} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \end{array}

Formule 10

Le panneau 2 est assigné à une classe de section 4, le flambement local n’est donc pas déterminant. Les largeurs efficaces du panneau 2 doivent être déterminées selon [1] , section 4.4.

La distribution des contraintes au niveau du panneau 2 est uniforme. Il en résulte un ratio de contraintes ψ = 1 et, selon le Tableau 4.1, une valeur de flambement de k_σ = 4,0. Pour l'élancement λ_p2, le résultat est, selon la Section 4.4 (2) [1] :

${\bar{λ}}_{p 2} = \frac{\frac{c_{2}}{t_{w}}}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{165, 8}{28, 4 \cdot 0, 814 \cdot \sqrt{4}} = 3, 588$ Formule 12	$> 0, 5 \sqrt{0.085 - 0, 055 \cdot ψ}$ Formule 13
	$> 0, 5 \sqrt{0.085 - 0.055 \cdot 1} = 0, 673$ Formule 14

Le facteur de réduction locale ρ est déterminé selon l'Équation (4.2) de [1] :

ρ_{2} = \frac{{\bar{λ}}_{p 2} - 0.055 \cdot (3 ψ)}{{\bar{λ}}_{p 2}^{2}} = \frac{3, 588 - 0, 055 \cdot (3 1)}{3, 588^{2}} = 0, 262 < 1

Formule 15

Les largeurs efficaces du panneau 2 sont calculées selon le Tableau 4.1 de [1], en prenant en compte le flambement local :

\begin{array}{l} b_{2, eff} = ρ_{2} \cdot c_{2} = 0, 262 \cdot 2.487, 5 = 650, 7 mm \\ b_{2, edge, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \\ b_{2, \sup, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \end{array}

Formule 16

Avec les largeurs de la section brute, on obtient :

\begin{array}{l} b_{2, edge} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \\ b_{2, \sup} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \end{array}

Formule 17

Comportement similaire à celui d’une dalle

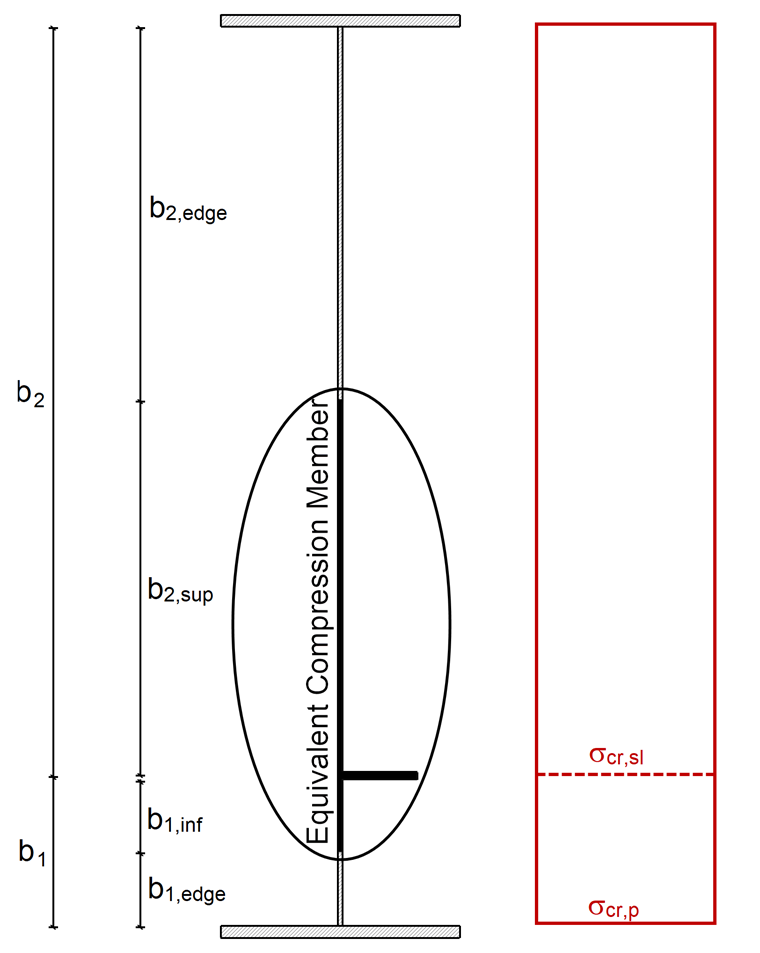
La contrainte critique de flambement du raidisseur σcr,sl est calculée selon l’Annexe A.2.2 de [1]. Il faut tout d’abord calculer la longueur efficace de la plaque a_c :

a_{c} = 4, 33 \cdot \sqrt[4]{\frac{I_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}}{t^{3} \cdot b}} = 4, 33 \cdot \sqrt[4]{\frac{11900 \cdot 50^{2} \cdot 250^{2}}{1, 5^{3} \cdot (50 250)}} = 896, 4 cm > a = 300 cm

Formule 18

La contrainte critique de flambement du raidisseur σ_cr,sl se traduit par a < a_c :

\begin{array}{l} σ_{cr, sl} = \frac{π^{2} \cdot E \cdot I_{sl, 1}}{A_{sl, 1} \cdot a^{2}} + \frac{E \cdot t^{3} \cdot b \cdot a^{2}}{4 \cdot π^{2} \cdot (1 - ν^{2}) \cdot A_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}} für a < a_{c} \\ σ_{cr, sl} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} + \frac{21.000 \cdot 1, 5^{3} \cdot (50 250) \cdot 300^{2}}{4 \cdot π^{2} \cdot (1 - 0, 3^{2}) \cdot 289, 4 \cdot 50^{2} \cdot 250^{2}} = 95, 9 kN / {cm}^{2} \end{array}

Formule 19

I_sl,1 et A_sl,1 représentent ici le moment d’inertie de la section brute et l’aire de la section brute de la barre comprimée équivalente selon [1] ; A.2.1(2) pour le flambement perpendiculaire au plan de la plaque ainsi que b₁ et b₂ sont les distances entre les raidisseurs et les bords longitudinaux (b₁ + b₂ = b).

La distribution des contraintes est uniforme. Par conséquent, la contrainte critique de flambement σ_cr,p correspond à la contrainte critique de flambement σ_cr,sl.

σ_{cr, p} = σ_{cr, sl} = 95, 9 kN / {cm}^{2}

Formule 20

Section brute de la barre équivalente comprimée

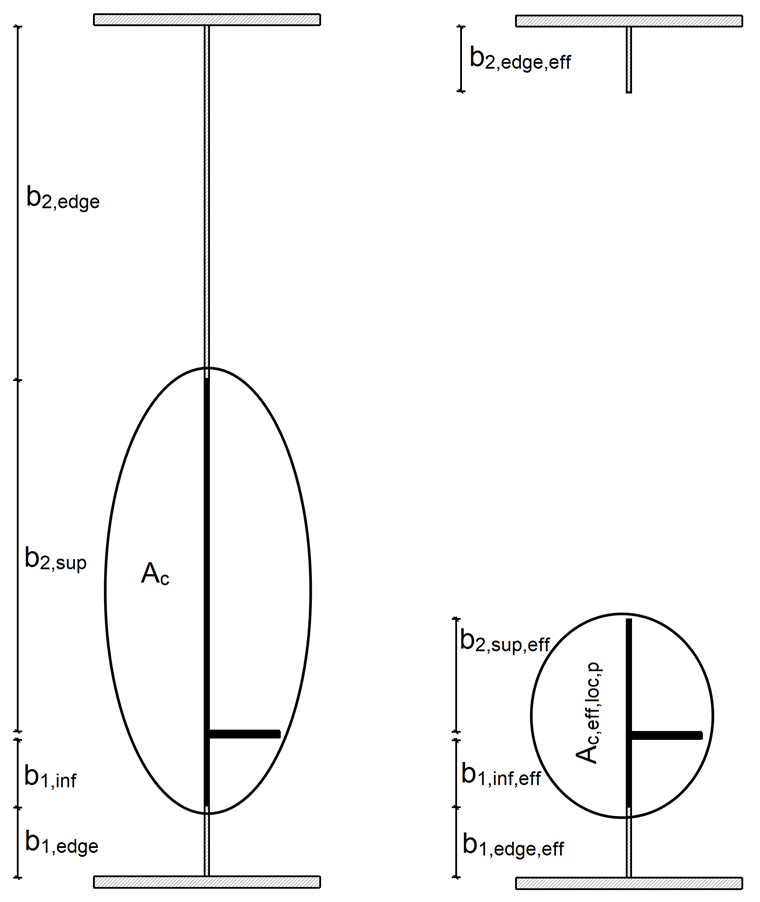
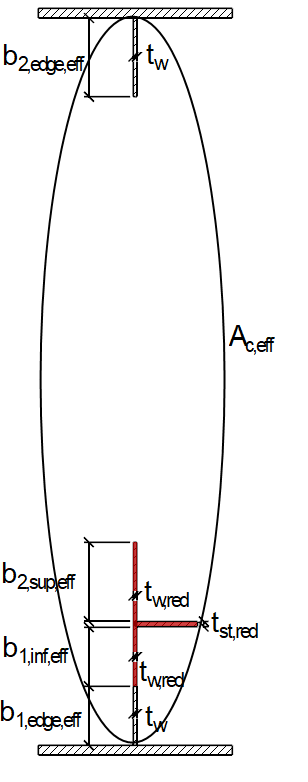
L’aire de la section brute A_c du panneau avec raidisseurs longitudinaux est calculée comme suit, en négligeant les plaques de bord supportées par un composant de plaque adjacent et l’aire de la section efficace A_{c, eff, loc,p} de l’aire décrite ci-dessus :

A_{c} = (b_{1, \inf} + b_{2, \sup} + t_{st}) \cdot t_{w} + b_{st} \cdot t_{st} = (24, 38 + 124, 38 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 289, 4 {cm}^{2}

Formule 21

La rigidité appartient à la classe de section 3, l’aire de section efficace de la rigidité correspond donc à l’aire de section brute de la rigidité.

A_{c, eff, loc, p} = (b_{1, \inf, eff} + b_{2, \sup, eff} + t_{st}) \cdot t_{w} + b_{st, eff} \cdot t_{st} = (24, 38 + 32, 54 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 151, 6 {cm}^{2}

Formule 22

Les valeurs de la section sont indiquées sur la Figure 04.

Section brute et efficace dues au flambement local

Le facteur de réduction β_a,c,p est calculé comme suit selon la section 4.5.2 de [1] :

\begin{array}{l} β_{a, c, p} = \frac{A_{c, eff, loc, p}}{A_{c}} \\ β_{a, c, p} = \frac{151, 6}{289, 4} = 0, 524 \end{array}

Formule 23

Selon l'Équation (4.7) de [1], l’élancement global λ_p du panneau raidi donne :

${\bar{λ}}_{p} = \sqrt{\frac{β_{a, c, p} \cdot f_{y}}{σ_{cr, p}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{95, 9}} = 0, 440$ Formule 25	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Formule 26
	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Formule 27

L’élancement λ_p est inférieur à la valeur limite de 0,673 selon 4.4(2) de [1]. Par conséquent, aucune réduction due au comportement de la dalle n’est nécessaire (par exemple, ρ_p = 1,0).

Comportement de flambement des plaques

La contrainte critique de flambement σ_cr,c est déterminée selon la section 4.5.3 (3) de [1]. Premièrement, la contrainte de flambement σ_cr,c,sl du raidisseur, positionnée au plus proche du bord le plus comprimé, est déterminée selon l’Équation (4.9) de [1].

σ_{cr, c, sl} = \frac{π^{2} \cdot E \cdot I_{sl}}{A_{sl} \cdot a^{2}} = \frac{π^{2} \cdot 21000 \cdot 11900}{289, 4 \cdot 300^{2}} = 94, 7 kN / {cm}^{2}

Formule 28

La distribution des contraintes est uniforme. La contrainte critique de flambement σ_cr,c correspond donc à la contrainte critique de flambement σ_cr,c,sl du raidisseur positionné au plus proche du bord le plus comprimé.

σ_cr,c = σ_cr,c,sl = 94,7 kN/cm²

Le facteur de réduction β_a,c,c est calculé comme suit selon la section 4.5.3(4) de [1] :

β_{a, c, c} = \frac{A_{sl, eff}}{A_{sl}} = \frac{151, 6}{289, 4} = 0, 524

Formule 29

Le coefficient d'élancement λcdes résultats de la barre équivalente comprimée, selon l'Équation (4.11) de [1] est :

{\bar{λ}}_{c} = \sqrt{\frac{β_{a, c, c} \cdot f_{y}}{σ_{cr, c}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{94, 7}} = 0, 443

Formule 31

Selon la section 4.5.3 (5) de [1] , le rayon de giration i est calculé comme suit :

i = \sqrt{\frac{I_{sl}}{A_{sl}}} = \sqrt{\frac{11.900}{289, 4}} = 6, 41 cm

Formule 32

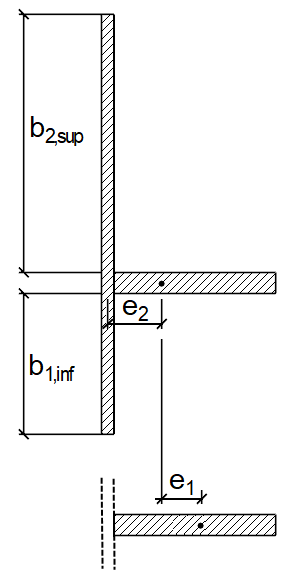
L’espacement e est le plus grand des deux espacements selon la Figure A.1 de [1] ; par exemple, soit l’espacement e₁ du raidisseur, ajusté entre le centre de gravité et considérée indépendamment de la plaque, soit l’espacement e₂ du centre de gravité de la plaque raidie au milieu de la plaque. Ces distances sont indiquées sur la Figure 05.

Barre de compression équivalente et raidisseur : Espacements e1, e2

e = max (e₁, e₂) = max(10,39 cm, 2,86 cm) = 10,39 cm

Le facteur d'imperfection αe est déterminé comme suit selon l'Équation (4.12) de [1] avec α = 0,49 pour les sections ouvertes avec raidisseurs :

α_{e} = α \frac{0, 09}{i / e} = 0, 49 \frac{0, 09}{6, 41 / 10, 39} = 0, 636

Formule 33

Le facteur de réduction χ_c est déterminé selon [3] , 6.3.1.2 :

\begin{array}{l} ϕ = 0, 5 \cdot (1, 0 α_{e} \cdot ({\bar{λ}}_{c} - 0, 2) {\bar{λ}}_{c}^{2}) = 0, 5 \cdot (1, 0 0, 636 \cdot (0, 443 - 0, 2) 0, 443^{2}) = 0, 675 \\ χ_{c} = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}_{c}^{2}}} = \frac{1}{0, 675 \sqrt{0, 675^{2} - 0, 443^{2}}} = 0, 844 < 1 \end{array}

Formule 34

Interpolation entre le flambement de plaque et le flambement de dalle

Le comportement structurel du panneau est déterminé à l'aide du facteur ξ, selon la Section 4.5.4(1) de [1] :

\begin{array}{l} ξ = \frac{σ_{cr, p}}{σ_{cr, c}} - 1 but 0 \leq ξ \leq 1 \\ ξ = \frac{95, 9}{94, 7} - 1 = 0, 013 \end{array}

Formule 35

Le facteur de réduction final ρc est déterminé à l'aide de l'équation d’interaction selon l'Équation (4.13) de [1] :

ρ_{c} = (ρ_{p} - χ_{c}) \cdot ξ \cdot (2 - ξ) + χ_{c} = (1 - 0, 844) \cdot 0, 013 \cdot (2 - 0, 013) + 0, 844 = 0, 848

Formule 36

Propriétés de la section efficace

L’aire de la section efficace de la zone comprimée A_c,eff du panneau raidi est calculée selon l’Équation (4.5) de [1] :

A_{c, eff} = ρ_{c} \cdot A_{c, eff, loc, p} + \sum b_{edge, eff} \cdot t = 0, 848 \cdot 151, 6 24, 38 \cdot 1, 5 + 32, 54 \cdot 1, 5 = 214, 1 cm ²

Formule 37

L’aire de la section efficace A_eff est :

A_{eff} = A_{c, eff} + 2 \cdot b_{f} \cdot t_{f} = 214, 1 + 2 \cdot 80 \cdot 4 = 854, 1 cm ²

Formule 38

Section efficace due au flambement local et global

Calcul des panneaux avec raidisseurs

Les axes du centre de gravité de la section brute et de la section efficace ne coïncident pas. Les moments fléchissants agissants additionnels dus au déplacement de l’axe de gravité de la section efficace lié à l’axe de gravité de la section brute doivent donc être pris en compte. Ces moments fléchissants additionnels sont calculés comme suit :

\begin{array}{l} e_{y} = 0, 82 - 0, 72 = 0, 10 cm \\ e_{z} = 164, 97 - 157, 42 = 7, 55 cm \\ M_{y} = N \cdot e_{z} = 4000 \cdot 7, 55 = 30202, 4 kNcm \\ M_{z} = N \cdot e_{y} = - 4000 \cdot 0, 10 = - 414, 3 kNcm \\ M_{u} = 30203, 7 KNcm \\ M_{v} = - 306, 4 KNcm \end{array}

Formule 39

La contrainte maximale est la suivante :

σ_{eff} = \frac{N}{A_{eff}} + \frac{M_{u} \cdot e_{v}}{I_{u, eff}} - \frac{M_{v} \cdot e_{u}}{I_{v, eff}} = \frac{4.000}{854, 1} + \frac{30.203, 7 \cdot 165, 12}{17.466.764} - \frac{- 306, 4 \cdot 40, 23}{352.626} = 5, 01 kN / cm ²

Formule 40

Le calcul est effectué comme suit selon l'Équation (4.15) de [1] :

η_{1} = \frac{σ_{eff}}{\frac{f_{y}}{γ_{M 0}}} = \frac{5, 01}{\frac{34, 5}{1, 0}} = 0, 15

Formule 41

Vérification du flambement par torsion

Selon la Section 9.2.1(8) de [1], le critère suivant doit être respecté de manière générale pour éviter le flambement par torsion des raidisseurs à sections ouvertes :

\begin{array}{l} η_{1} = \frac{5, 3 \cdot f_{y} \cdot I_{p}}{E \cdot I_{S t . V e n}} \leq 1 \\ η_{1} = \frac{5, 3 \cdot 34, 5 \cdot 13.053}{21.000 \cdot 122} = 0, 93 \leq 1 \end{array}

Formule 42

I_p and I_St.Ven décrivent le moment d’inertie polaire et l’inertie de torsion de Saint-Venant de la section raidie seule (sans plaque), calculé autour du point de connexion avec la plaque.

Si la rigidité de gauchissement est prise en compte, la contrainte de flambement critique par torsion σ_cr doit être déterminée en premier. Cette valeur est calculée selon les Équations (2.119) et (2.120) de [4] comme suit :

\begin{array}{l} σ_{cr 1} = \frac{1}{I_{p}} \cdot (\frac{π^{2} \cdot E \cdot I_{ω}}{l^{2}} + G \cdot I_{St . Ven}) für l < L_{cr} \\ σ_{cr 2} = \frac{1}{I_{p}} \cdot (2 \cdot \sqrt{C_{θ} \cdot E \cdot I_{ω}} + G \cdot I_{St . Ven}) für l > L_{cr} \end{array}

Formule 43

La rigidité présente une constante de gauchissement I_ω = 0 cm⁶. La contrainte critique de flambement par torsion σ_cr est alors simplifiée comme suit :

\begin{array}{l} σ_{cr 1} = σ_{cr 2} = \frac{1}{I_{p}} \cdot G \cdot I_{S t . V e n} \\ σ_{cr 1} = σ_{cr 2} = \frac{1}{13.053} \cdot 8.077 \cdot 122 = 75, 5 kN / cm ² \end{array}

Formule 44

I_p and I_St.Ven décrivent le moment d'inertie polaire et l'inertie de torsion de Saint-Venant du raidisseur seul, calculé autour du point de raccord avec la plaque.

Selon la Section 9.2.1(9) de [1], le critère dans 9.2.1(8) ou le critère suivant ne doit généralement pas être négligé lorsque l’on tient compte de la rigidité de gauchissement :

\begin{array}{l} η_{2} = \frac{θ \cdot f_{y}}{σ_{cr 1}} \leq 1 \\ η_{3} = \frac{θ \cdot f_{y}}{σ_{cr 2}} \leq 1 \end{array}

Formule 45

À l'aide d'un facteur assurant le comportement élastique selon la classe de section 3 d’après [5] de θ = 2 f pour les raidisseurs présentant une faible rigidité de gauchissement (barre plate ou acier plat à boudin), on obtient le résultat suivant :

η_{2} = η_{3} = \frac{2 \cdot 34, 5}{75.5} = 0, 91 \leq 1

Formule 46

La vérification du flambement par torsion est donc achevée.

SHAPE-THIN

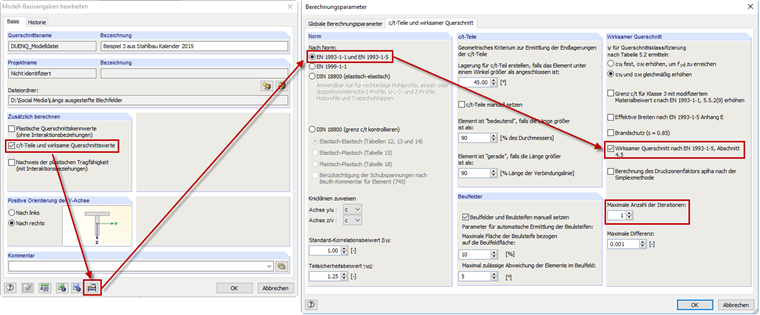
Dans SHAPE-THIN, le calcul des plaques avec raidisseurs peut être effectué selon la section 4.5 de [1]. Le panneau de contrôle « Parties c/t et propriétés des sections efficaces » doit être activé dans les données générales. « EN 1993-1-1 et EN 1993-1-5 » doivent ensuite être sélectionnés dans les paramètres de calcul ; le panneau de contrôle « Section efficace selon l'EN 1993-1-5, Section 4.5 » doit également être sélectionné. La détermination des largeurs efficaces doit être effectuée dans un processus itératif selon la Section 4.4(3) de [1]. Dans cet exemple, une seule itération doit être utilisée pour le calcul dans SHAPE-THIN (voir la Figure 07).

Paramètres de calcul

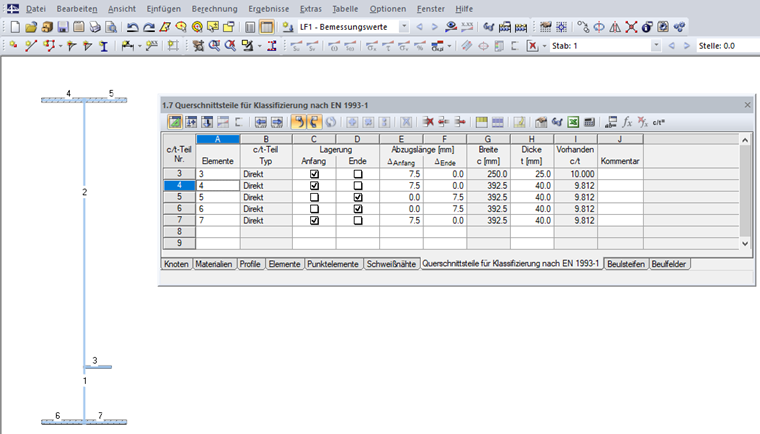
Les éléments de la section doivent d’abord avoir été saisis. Les parties c/t sont généralement générées automatiquement à partir des conditions géométriques, elles peuvent cependant être créées dans le tableau « 1.7 Parties de la section pour la classification selon l'EN 1993-1 » (voir la Figure 08) ou la boîte de dialogue correspondante.

Parties de la section pour la classification

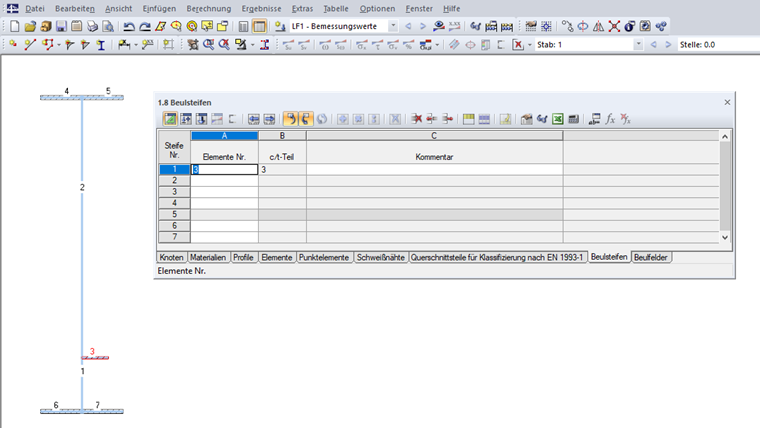
Les raidisseurs peuvent ensuite être définis dans le Tableau « 1.8 Raidisseurs » ou dans la boîte de dialogue correspondante (voir la Figure 09).

Raidisseurs

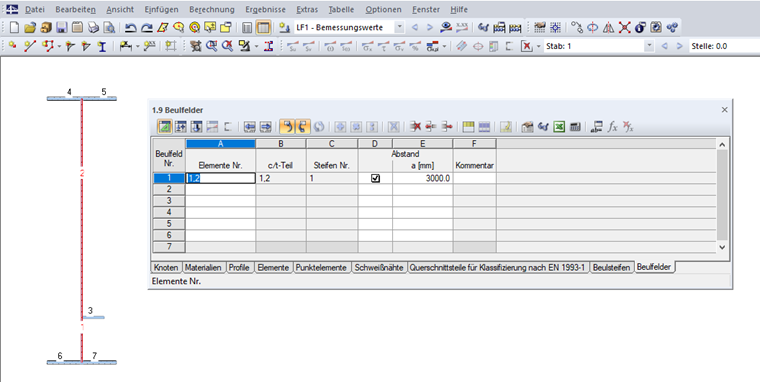
De plus, le panneau raidi doit être spécifié dans le Tableau « 1.9 Panneaux raidis » (voir la Figure 10) ou la boîte de dialogue correspondante. Les éléments du panneau raidi doivent être sélectionnés et l'espacement des raidisseurs transversaux a doit être saisi. Si aucune distance n'est définie pour les raidisseurs transversaux, la valeur a = 10 000 mm est appliquée pour le calcul. Les raidisseurs dans le panneau sont identifiés automatiquement. Les extrémités du panneau doivent être soutenues, ce qui signifie qu’un appui est nécessaire.

Panneaux de flambement

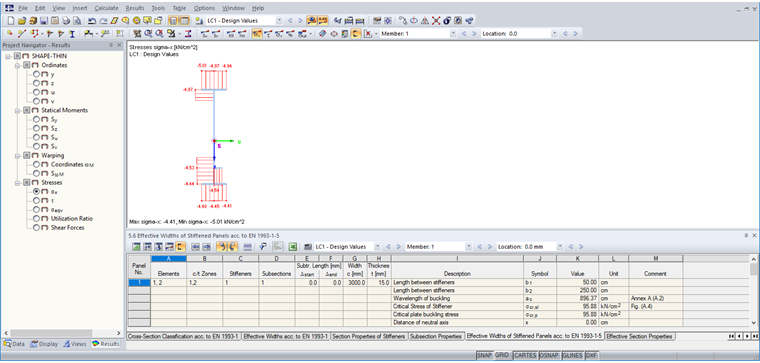
Les résultats de la section efficace peuvent être affichés à l'aide du bouton « Largeurs efficaces ».

Résultats

Auteur

Mme von Bloh fournit une assistance technique à nos utilisateurs et est également responsable du développement du programme SHAPE-THIN et de la construction en acier et en aluminium.

Liens

Logiciels de calcul de structures en acier

Références

Eurocode 3 : calcul des structures en acier - Partie 1-5 : Plattenförmige Bauteile. Beuth Verlag GmbH, Berlin, 2010.
Beg, D.; Kuhlmann, U.; Davaine, L.; Braun, B.: Design of Plated Structures. Eurocode 3: Design of Steel Structures. Part 1-5 Design of Plated Structures. Berlin: Ernst & Sohn, 2011
Kuhlmann, U.: Stahlbau-Kalender 2015 - Eurocode 3 - Grundnorm, Leichtbau. Berlin: Ernst & Sohn, 2015
Johansson, B.; Maquoi, R.; Sedlacek, G.; Müller, C.; Beg, D.: Commentary and Worked Examples to EN 1993-1-5, Plated Structural Elements. Luxemburg: Office for Official Publications of the European Communities, 2007
Eurocode 3 : Bemessung und Konstruktion von Stahlbauten − Teil 1-1: Règles générales et règles pour les bâtiments. Beuth Verlag GmbH, Berlin, 2010

Téléchargements

Fichier de modèle SHAPE-THIN

308 KB

Flambement de sous-panneau Flambement de plaque raidie

Avez-vous des questions ?

Evénements

24.07.2024

Analyse de stabilité linéaire dans RFEM 6 et RSTAB 9

Webinaire

Analyse de stabilité linéaire dans RFEM 6 et RSTAB 9

22.08.2024

Vérification des assemblages acier dans RFEM 6 à l'aide d'un exemple pratique

Webinaire

Vérification des assemblages acier dans RFEM 6 à l'aide d'un exemple pratique

06.11.2024

Formation en ligne

RFEM6 | Étudiants | Introduction à la vérification de l'acier

Vidéos

Foire aux questions (FAQ)

[FR] FAQ 003156 | Lors du calcul, je reçois un avertissement indiquant que certains éléments sont connectés à ...

Longueur: 00:00:52 min

Événement

Matinale de Dlubal Software | Fonctionnalités avancées pour les assemblages en acier dans RFEM 6

Longueur: 00:32:16 min

Fonctionnalité de produit

Composant « Platine d’assise » pour les assemblages de bloc de fondation

Longueur: 00:00:42 min

Événement

Webinaire | Intégration de Tekla Structures dans RFEM 6

Longueur: 00:52:56 min

Événement

Webinaire | Modélisation et calcul de structures en acier dans RFEM 6 | Partie 2 : Combinaisons, Calcul, Documentation

Longueur: 01:08:12 min

Événement

Webinaire | Modélisation et calcul de structure acier dans RFEM 6 | Partie 1 : Modélisation, entrée de charge

Longueur: 00:58:00 min

Événement

Webinaire | Considération des phases de construction dans RFEM 6

Longueur: 00:55:53 min

Webinaire | Vérification d'un chapiteau industriel en profilés aluminium dans RFEM 6

Événement

Webinaire | Étapes de construction dans les structures en toile tendue dans RFEM 6

Longueur: 01:02:19 min

Événement

Webinaire | Vérification des assemblages acier dans RFEM 6 selon l'AISC 360-22

Longueur: 01:02:00 min

Playlist

Modèles à télécharger

Appui métallique pour panneaux photovoltaïques dans RFEM 6

49x

14x

Support métallique pour panneaux photovoltaïques

170x

70x

hangar en acier

38x

Construction du pavillon au Zoo Tabor

Modèle 004954 | Assemblages d'une ombrière photovoltaïque

213x

83x

Assemblages d'une ombrière photovoltaïque

Modèle 004984 | Bâtiment en acier à un étage

98x

30x

Structure en acier | Intégration de Tekla

Modèle 004972 | Structure de scène avec différents assemblages en acier

359x

153x

Structure de scène avec différents assemblages en acier

Modèle 004976 | Poutres en I d'assemblage en acier

141x

30x

Assemblage en acier d'une poutre en I à un poteau avec des raidisseurs

Modèle 004969 | Poutre en porte-à-faux en acier

98x

18x

Poutre en porte-à-faux en acier

83x

19x

Balcon étendu

Articles de la base de connaissance

Lire la suite

KB 001883 | Plate Girder Design According to AISC 360-22 in RFEM 6

La poutre à âme pleine est un choix économique pour la construction avec de longues travées. Les poutre à âme pleine en acier avec section en I ont généralement une âme profonde pour tirer le meilleur parti de leur résistance au cisaillement et de l'espacement entre les semelles, mais l'âme est mince pour réduire le poids propre. En raison de son important rapport hauteur/épaisseur (h/t_w), des raidisseurs transversaux peuvent être nécessaires pour rigidifier l'âme élancée.

Lire la suite

Rigidité des assemblages acier et son influence sur le calcul des structures

La considération de la rigidité des assemblages en acier est cruciale dans le calcul de structure. Les assemblages sont souvent traités comme strictement articulés ou rigides, ce qui peut entraîner des vérifications peu économiques, voire dangereuse. Découvrez comment le logiciel RFEM et le module complémentaire Assemblages acier de Dlubal Software permettent de vérifier la rigidité des assemblages et la résistance au moment, permettant ainsi des vérifications plus sûres et plus économiques.

Lire la suite

ko 001875 | AISC 341-22 Vérification des barres de portiques résistants à la flexion dans RFEM 6

Les trois types de portiques résistants à la flexion (ordinaire, intermédiaire, spécial) sont disponibles dans le module complémentaire Vérification de l'acier de RFEM 6. Le résultat de l'analyse de sismicité selon l'AISC 341-22 est divisé en deux sections : les exigences pour les barres et les exigences pour les assemblages.

Lire la suite

Fonctionnalités de produit

Module complémentaire « Assemblages acier pour RFEM 6 » | Bibliothèque de composants

De nombreux types de composants tels que des platines de base et d'about, des cornières d'âme, des plaques de connexion, des goussets, des raidisseurs, des jarrets ou des nervures pour une entrée facile des situations d'assemblage typiques
Composants de base universellement applicables (par ex. des plaques, des soudures, des boulons, des plans auxiliaires) pour la modélisation de situations d'assemblage complexes
Affichage graphique de la géométrie de l'assemblage avec actualisation dynamique lors de l'entrée
Large éventail de formes de section : Sections en I, sections en U, cornières, sections en T, sections creuses, sections composées et sections à parois minces
Bibliothèque dans le Dlubal Center avec un grand nombre de modèles de connexion côté programme, y compris des modèles définis par l'utilisateur
La géométrie de l'assemblage est automatiquement adaptée en fonction de la disposition relative des composants, même en cas de modification ultérieure des composants structuraux.

Lire la suite

Fonctionnalité 002820 | Déformation plastique limite pour les cordons de soudure

Dans la configuration pour l'ELU de la vérification des assemblages acier, vous avez la possibilité de modifier la déformation plastique ultime des soudures.

Lire la suite

Le composant « Platine d’assise » permet de vérifier des assemblages avec une platine et des ancrages coulés dans la fondation. Les plaques, les cordons de soudures, les ancrages et l’interaction acier-béton sont analysés.

Lire la suite

Fonctionnalité 002807 | Affichage 3D des résultats FSM

La boîte de dialogue « Modifier la section » permet d'afficher les modes de flambement selon la méthode des bandes finies (FSM) comme graphique tridimensionnel.

Lire la suite

Foire aux Questions (FAQ)

Quelle est la différence entre SHAPE-THIN 9 et SHAPE-THIN 8 ?

Est-il possible de modéliser des sections formées à froid dans SHAPE-THIN 8 et de les vérifier dans RF-/STEEL Cold-Formed Sections ?

Lors du calcul, un avertissement indique que certains éléments sont connectés au panneau de flambement, mais qu'ils ne sont pas définis comme des raidisseurs (voir la Figure 01). Que faire dans ce cas précis ?

Qu’est ce que la méthode des éléments finis basée sur les composants (CBFEM) ?

Est-il possible d’effectuer des analyses de stabilité selon l’EN 1993-1-1 dans RSECTION 1 ?

Pourquoi la plaque que je souhaite couper/modifier dans n’est-elle pas modifiable dans l’éditeur de plaques/coupe de plaque ?

Projets clients

Modèle RFEM avec les contraintes de membrane

Toiture à membrane de la tribune de l'Université technique de Xuzhou, Chine

CP 001302 | Vue extérieure de l’extension d’entrepôt industriel

Extension d’entrepôt industriel à Bressuire, France

Vue extérieure de l'unité de production et de stockage de viennoiseries | © GH HERVOUET

Création d'une unité de production et de stockage de viennoiseries à Montbert, France

Gare de péage éclairée | © M. Yunchao Ding, Jiangsu Jingong être Structure Co., Ltd.

Gare de péage de Dawang, Shaanxi, Chine

Modèle RFEM de l'entrepôt à rayonnages hauts avec résultats des déformations

Entrepôt à rayonnages en hauteur, Chine

Station multi-énergies aux Sables-d’Olonne, France

Vue de face du bâtiment avec les poteaux mixtes en acier en forme de V | © Tragwerker GmbH

Immeuble de bureaux avec centre visiteurs et parking à Geiselbullach, Allemagne

Pergola métallique de l'Université Rafael Landívar (© Ing. Enrique de León)

Pergola en acier sur la Plaza del Edificio L, Université Rafael Landívar, Guatemala

Tour du Radar à gauche (© SAQQERA Ingeniería)

Calcul de structure de la tour radar de l'aéroport de Málaga, Espagne

Produits recommandés pour vous

RFEM6 | Logiciel de base RFEM 6

RFEM 6

Logiciel de base

La nouvelle génération de logiciels aux éléments finis est utilisée pour le calcul de structures composées de barres, de surfaces et de solides.

Prix de la licence initiale 4 170,00 USD

RFEM6 | Vérification

Vérification de l'acier pour RFEM 6

Module complémentaire

Le module complémentaire Vérification de l'acier permet d'effectuer les vérifications à l'état limite ultime et à l'état limite de service des barres en acier selon diverses normes.

Prix de la licence initiale 2 550,00 USD

RFEM6 | Assemblages

Assemblages acier pour RFEM 6

Module complémentaire

Le module complémentaire Assemblages acier pour RFEM vous permet d'analyser les assemblages acier à l'aide d'un modèle EF. La modélisation s'exécute de manière entièrement automatique en arrière-plan et peut être contrôlée via la saisie simple et familière des composants.

Prix de la licence initiale 2 110,00 USD