Voltar para a base de dados de conhecimento

7881x

001536

Sonja von Bloh, M.Sc.

2018-09-12

Painéis reforçados longitudinalmente segundo a EN 1993-1-5, Secção 4.5

No SHAPE-THIN é possível realizar o cálculo de painéis reforçados longitudinalmente de acordo com a Secção 4.5 da norma EN 1993-1-5. Para painéis reforçados longitudinalmente têm de ser consideradas as superfícies efectivas devido à encurvadura local dos painéis singulares na laje e nos reforços, bem como as superfícies efetivas de todo o painel de encurvadura do reforço de todo o painel.

Em primeiro lugar, as superfícies efetivas dos painéis singulares são determinadas através do fator de redução de acordo com a EN 1993-1-5 [1] , Secção 4.4, para ter em consideração a encurvadura dos painéis singulares. Numa segunda etapa, a segurança de encurvadura de todo o painel é determinada tendo em consideração o comportamento de encurvadura similar ao das encurvadura das barras. Com o fator de redução de todo o painel de encurvadura, as larguras efetivas do painel singular são novamente reduzidas. Isto resulta numa secção eficaz que pode ser gerida como secção da classe 3.

Exemplo

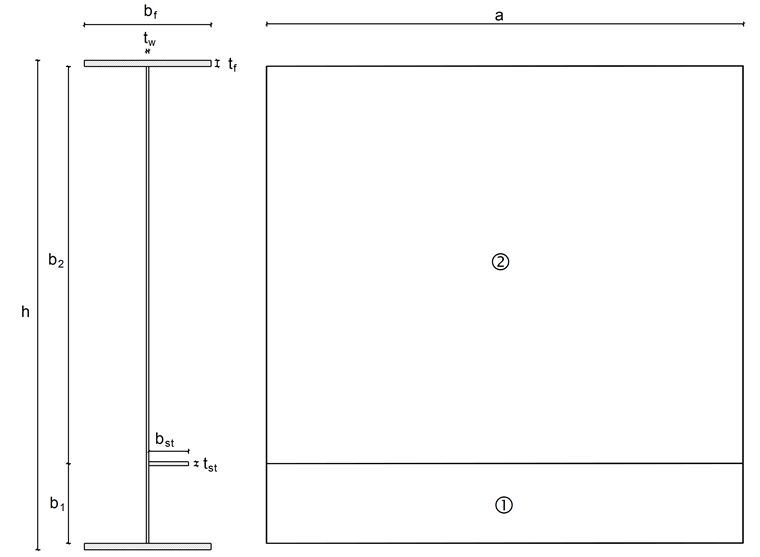
O exemplo seguinte é retirado do Anuário de estruturas em Aço de 2015 [2]. A secção consiste numa viga em I cuja alma é reforçada por um reforço transversal rígido e um reforço longitudinal. Os reforços transversais são dispostos numa distância de 3,000 mm entre estes e o reforço longitudinal é soldado a uma distância de 500 mm do banzo inferior. As soldaduras são ignoradas. Uma força de compressão axial de N_Ed = 4,000 kN está a atuar.

secção

Material:
S355 J0
f_y = 35,5 kN/cm² (para t ≤ 3 mm e t ≤ 16 mm)
f_y = 34,5 kN/cm² (para t >16 mm e t ≤ 40 mm)
E= 21 000 kN/cm²
G = 8076,92 kN/cm²
γ_M0 = 1,0

a = 3,000 mm
_b1 = 500 mm
_b2 = 2500 mm
b_f = 800 mm
b_st = 250 mm
t_w = 15 mm
t_f = 40 mm
t_st = 25 mm
h = 3,080 mm

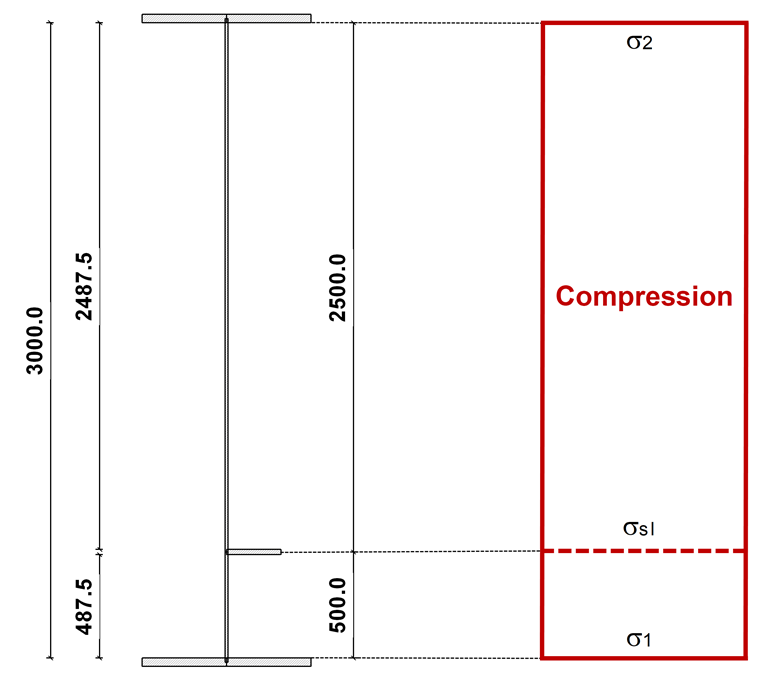
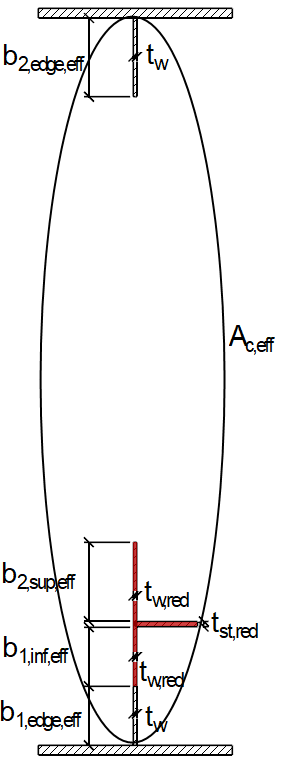
Secção bruta e distribuição de tensões

A tensão é calculada da seguinte forma:

σ_{1} = σ_{sl} = σ_{2} = \frac{N_{Ed}}{A} = \frac{4, 000}{1, 152.5} = 3.47 kN / cm ²

Fórmula 1

A secção bruta e a distribuição de tensões são apresentadas na Figura 02.

distribuição de tensões

Classificação da secção

Durante a classificação da secção, é avaliado se é necessário o dimensionamento de uma encurvadura para painéis singulares. Se o painel é pelo menos de secção classe 3, encurvadura local não é determinante.

corda

\begin{array}{l} c_{f} = \frac{b_{f} - t_{w}}{2} = \frac{800 - 15}{2} = 392.5 mm \\ \frac{c_{f}}{t_{f}} = \frac{392.5}{40} = 9.8 \end{array}

Fórmula 2

A relação c/t máxima λ_i é determinada de acordo com EN 1993-1-1 [3] , Tabela 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0.825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0.825 = 7.4 < \frac{c_{f}}{t_{f}} = 9.8 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0.825 = 8.2 < \frac{c_{f}}{t_{f}} = 9.8 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0.825 = 11.6 > \frac{c_{f}}{t_{f}} = 9.8 \end{array}

Fórmula 3

O banzo tem de ser atribuído com secção de classe 3. A encurvadura local não é determinante e não é necessária redução deste painel.

Alma

\begin{array}{l} c_{1} = b_{1} - \frac{t_{st}}{2} = 500 - \frac{25}{2} = 487.5 mm \\ \frac{c_{1}}{t_{w}} = \frac{487.5}{15} = 32.5 \end{array}

Fórmula 4

A relação c/t máxima λ_i é determinada de acordo com [3] , Tabela 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0.814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0.814 = 26.8 < \frac{c_{1}}{t_{w}} = 32.5 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0.814 = 30.9 < \frac{c_{1}}{t_{w}} = 32.5 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0.814 = 34.2 > \frac{c_{1}}{t_{w}} = 32.5 \end{array}

Fórmula 5

O painel 1 tem de ser atribuído com a classe 3 de secção. A encurvadura local não é determinante e não é necessária redução deste painel.

\begin{array}{l} c_{2} = b_{2} - \frac{t_{st}}{2} = 2, 500 - \frac{25}{2} = 2, 487.5 mm \\ \frac{c_{2}}{t_{w}} = \frac{2, 487.5}{15} = 165.8 \end{array}

Fórmula 6

A relação c/t máxima λ_i é determinada de acordo com [3] , Tabela 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0.814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0.814 = 26.8 < \frac{c_{2}}{t_{w}} = 165.8 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0.814 = 30.9 < \frac{c_{2}}{t_{w}} = 165.8 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0.814 = 34.2 < \frac{c_{2}}{t_{w}} = 165.8 \end{array}

Fórmula 7

O painel 2 tem de ser atribuído com secção de classe 4. A encurvadura local é determinante para este painel e é necessária a redução deste painel.

Reforço

\begin{array}{l} b_{st} = 250 mm \\ \frac{b_{st}}{t_{st}} = \frac{250}{25} = 10 \end{array}

Fórmula 8

A relação c/t máxima λ_i é determinada de acordo com [3] , Tabela 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0.825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0.825 = 7.4 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0.825 = 8.2 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0.825 = 11.6 > \frac{b_{st}}{t_{st}} = 10 \end{array}

Fórmula 9

A alma tem de ser atribuída com secção de classe 3. A encurvadura local não é determinante e não é necessária redução deste painel.

Larguras efetivas

O painel 1 é atribuído com secção de classe 3 por isso a encurvadura local não é determinante. Os valores da secção efetiva correspondem aos valores da secção bruta. De acordo com [1] , Tabela 4.1, isto resulta nas seguintes larguras efetivas:

\begin{array}{l} b_{1, eff} = c_{1} = 487.5 mm \\ b_{1, edge, eff} = b_{1, edge} = 0.5 \cdot c_{1} = 0.5 \cdot 487.5 = 243.8 mm \\ b_{1, \inf, eff} = b_{1, \inf} = 0.5 \cdot c_{1} = 0.5 \cdot 487.5 = 243.8 mm \end{array}

Fórmula 10

O painel 2 é atribuído com secção de classe 4 por isso a encurvadura local é determinante. As larguras efectivas do painel 2 tem de ser determinadas de acordo com [1] , Secção 4.4.

A distribuição de tensões no painel 2 é uniforme. Isto resulta numa relação de tensões de ψ = 1 e, de acordo com a Tabela 4.1, num valor de encurvadura de k_σ = 4,0. De acordo com [1] , Secção 4.4(2), o resultado para a relação de esbelteza λ_p2 é:

${\bar{λ}}_{p 2} = \frac{\frac{c_{2}}{t_{w}}}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{165.8}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 3.588$ Fórmula 12	$> 0.5 \sqrt{0.085 - 0.055 \cdot ψ}$ Fórmula 13
	$> 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673$ Fórmula 14

O fator de redução local ρ é determinado de acordo com [1] , Equação (4.2):

ρ_{2} = \frac{{\bar{λ}}_{p 2} - 0.055 \cdot (3 ψ)}{{\bar{λ}}_{p 2}^{2}} = \frac{3.588 - 0.055 \cdot (3 1)}{3 . 588^{2}} = 0.262 < 1

Fórmula 15

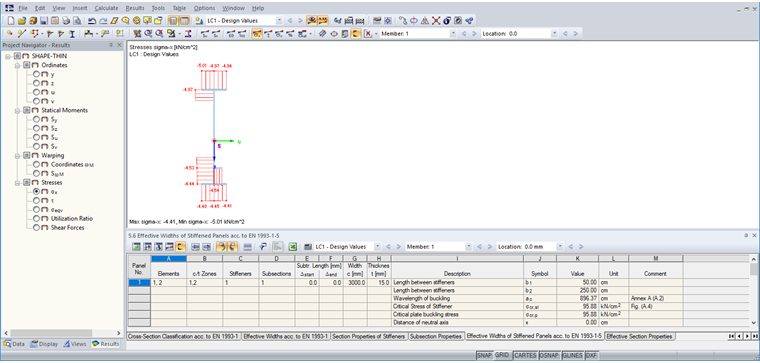
As larguras efetivas do painel 2, tendo em consideração a encurvadura local, são calculadas de acordo com [1] , Tabela 4.1:

\begin{array}{l} b_{2, eff} = ρ_{2} \cdot c_{2} = 0.262 \cdot 2, 487.5 = 650.7 mm \\ b_{2, edge, eff} = 0.5 \cdot b_{2, eff} = 0.5 \cdot 650.7 = 325.4 mm \\ b_{2, \sup, eff} = 0.5 \cdot b_{2, eff} = 0.5 \cdot 650.7 = 325.4 mm \end{array}

Fórmula 16

As larguras da secção bruta resultam em:

\begin{array}{l} b_{2, edge} = 0.5 \cdot c_{2} = 0.5 \cdot 2, 487.5 = 1, 243.8 mm \\ b_{2, \sup} = 0.5 \cdot c_{2} = 0.5 \cdot 2, 487.5 = 1, 243.8 mm \end{array}

Fórmula 17

Comportamento das lajes

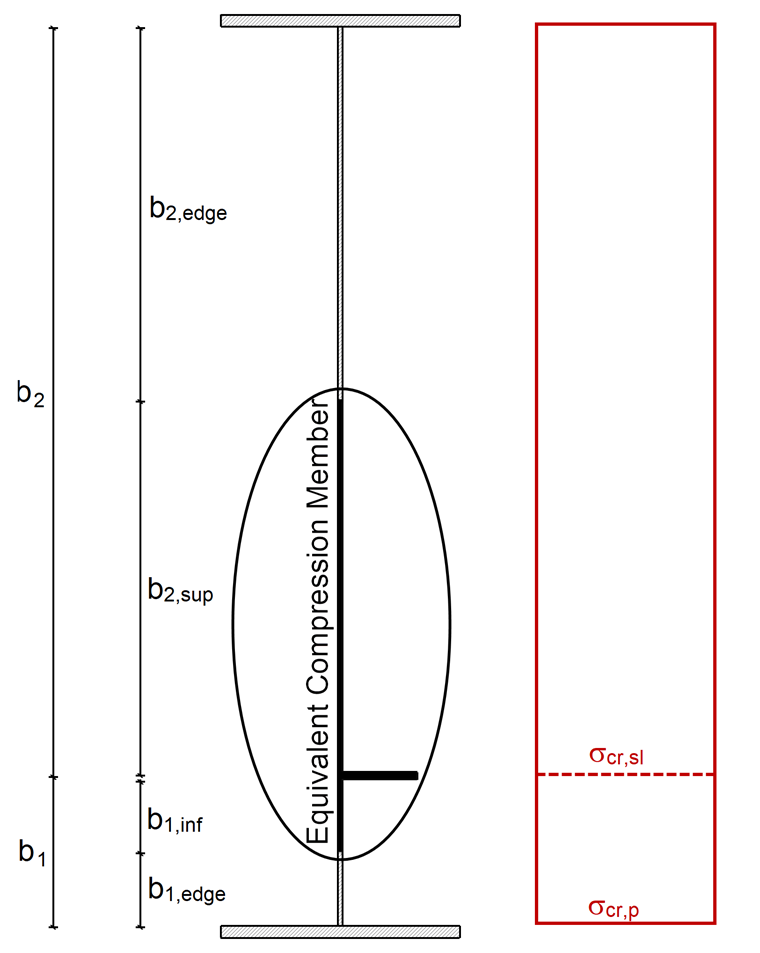
A tensão de encurvadura elástica crítica da rigidez σcr,sl é calculada de acordo com [1] , Anexo A.2.2. O comprimento efetivo do reforço a_c tem de ser calculado primeiro:

a_{c} = 4.33 \cdot \sqrt[4]{\frac{I_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}}{t^{3} \cdot b}} = 4.33 \cdot \sqrt[4]{\frac{11, 900 \cdot 50^{2} \cdot 250^{2}}{1 . 5^{3} \cdot (50 250)}} = 896.4 cm > a = 300 cm

Fórmula 18

A tensão de encurvadura elástica crítica do reforço σ_cr,sl resulta com a < a_c in:

\begin{array}{l} σ_{cr, sl} = \frac{π^{2} \cdot E \cdot I_{sl, 1}}{A_{sl, 1} \cdot a^{2}} + \frac{E \cdot t^{3} \cdot b \cdot a^{2}}{4 \cdot π^{2} \cdot (1 - ν^{2}) \cdot A_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}} für a < a_{c} \\ σ_{cr, sl} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} + \frac{21.000 \cdot 1, 5^{3} \cdot (50 250) \cdot 300^{2}}{4 \cdot π^{2} \cdot (1 - 0, 3^{2}) \cdot 289, 4 \cdot 50^{2} \cdot 250^{2}} = 95, 9 kN / {cm}^{2} \end{array}

Fórmula 19

I_sl,1 e A_sl,1 representam aqui o segundo momento da área da secção bruta e a área da secção bruta da barra de compressão equivalente de acordo com [1] ; A.2.1(2) para encurvadura perpendicular ao plano da laje, bem como b₁ e b₂ descrever as distâncias dos reforços às bordas longitudinais (b₁ + b₂ = b).

A distribuição da tensão é uniforme. Portanto, a tensão de encurvadura elástica da placa σcr_,p corresponde à tensão de encurvadura crítica σcr_,sl.

σ_{cr, p} = σ_{cr, sl} = 95.9 kN / {cm}^{2}

Fórmula 20

Maioria da secção da barra de compressão equivalente

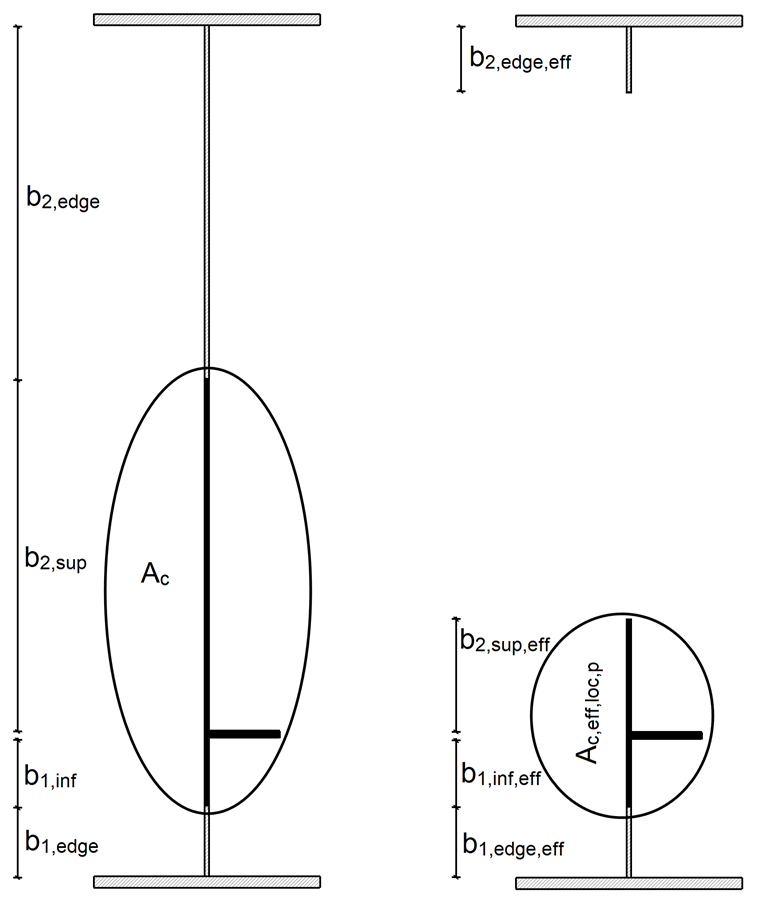
A área da secção bruta Ac do painel da placa reforçada longitudinalmente sem ter em conta as placas de extremidade apoiadas por um componente de placa adjacente e a área da secção efetiva A_c_,eff,loc,p da área descrito acima:

A_{c} = (b_{1, \inf} + b_{2, \sup} + t_{st}) \cdot t_{w} + b_{st} \cdot t_{st} = (24, 38 + 124, 38 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 289, 4 {cm}^{2}

Fórmula 21

O reforço pertence à secção de classe 3 por isso a área da secção efetiva do reforço corresponde à área da secção bruta do reforço.

A_{c, eff, loc, p} = (b_{1, \inf, eff} + b_{2, \sup, eff} + t_{st}) \cdot t_{w} + b_{st, eff} \cdot t_{st} = (24, 38 + 32, 54 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 151, 6 {cm}^{2}

Fórmula 22

Os valores da secção são apresentados na Figura 04.

Maioria da secção e efetiva devido à encurvadura local

O coeficiente de redução β_a,c,p é calculado de acordo com [1] , Secção 4.5.2, como se segue:

\begin{array}{l} β_{a, c, p} = \frac{A_{c, eff, loc, p}}{A_{c}} \\ β_{a, c, p} = \frac{151.6}{289.4} = 0.524 \end{array}

Fórmula 23

A esbelteza global λ_p da chapa reforçada de acordo com [1] , Equação (4.7), resulta em:

${\bar{λ}}_{p} = \sqrt{\frac{β_{a, c, p} \cdot f_{y}}{σ_{cr, p}}} = \sqrt{\frac{0.524 \cdot 35.5}{95.9}} = 0.440$ Fórmula 25	$< 0.5 \sqrt{0.085 - 0.055 \cdot ψ}$ Fórmula 26
	$< 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673$ Fórmula 27

De acordo com [1] , 4.4 (2), a relação de esbelteza λ_p é menor do que o valor limite 0,673. Portanto, não é necessária redução devido ao comportamento da laje; por exemplo, ρ_p = 1,0.

Comportamento da encurvadura local

A tensão de encurvadura crítica elástica_σcr,c é determinada de acordo com [1] , Secção 4.5.3(3). Em primeiro lugar, a tensão de encurvadura σ_cr,c,sl do reforço, que está posicionado na extremidade de compressão com carga máxima, é determinada de acordo com [1] , Equação (4.9).

σ_{cr, c, sl} = \frac{π^{2} \cdot E \cdot I_{sl}}{A_{sl} \cdot a^{2}} = \frac{π^{2} \cdot 21, 000 \cdot 11, 900}{289.4 \cdot 300^{2}} = 94.7 kN / {cm}^{2}

Fórmula 28

A distribuição da tensão é uniforme. Portanto, a tensão de encurvadura crítica elástica_σcr,c corresponde à tensão de encurvadura elástica σcr_,c,sl do reforço que é colocado na extremidade com força de compressão máxima.

σ_cr,c = σ_cr,c,sl = 94,7 kN/cm²

O coeficiente de redução β_a,c,c é calculado de acordo com [1] , Secção 4.5.3(4) do seguinte modo:

β_{a, c, c} = \frac{A_{sl, eff}}{A_{sl}} = \frac{151.6}{289.4} = 0.524

Fórmula 29

A relação de esbelteza λcda barra de compressão equivalente resulta, de acordo com [1] , Equação (4.11 ), em:

{\bar{λ}}_{c} = \sqrt{\frac{β_{a, c, c} \cdot f_{y}}{σ_{cr, c}}} = \sqrt{\frac{0.524 \cdot 35.5}{94.7}} = 0.443

Fórmula 31

De acordo com [1] , Secção 4.5.3(5), o raio de giração i é calculado da seguinte forma:

i = \sqrt{\frac{I_{sl}}{A_{sl}}} = \sqrt{\frac{11, 900}{289.4}} = 6.41 cm

Fórmula 32

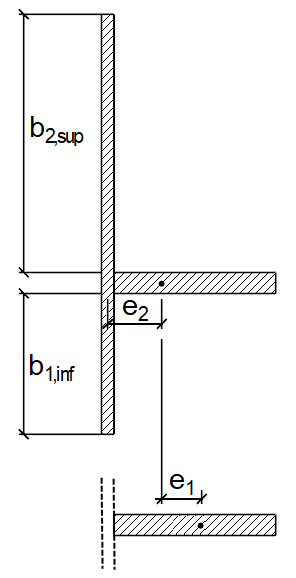
A distância e é a maior das duas distâncias de acordo com [1] , Figura A.1; por exemplo, quer a distância e₁ de um único reforço, ajustado entre o centro de gravidade e considerado independente da placa, sem a largura efectiva ao eixo do centro geométrico da placa de reforço ou a distância e₂ do eixo do centro geométrico da placa de reforço painel com o plano central da chapa. As distâncias são apresentadas na Figura 05.

Barra de compressão equivalente e reforço: Distâncias e1, e2

e = máx (e₁, e₂ ) = máx (10,39 cm, 2,86 cm) = 10,39 cm

O fator de imperfeição αe é determinado de acordo com [1] , Equação (4.12) com α = 0.49, para secções abertas de reforço do seguinte modo:

α_{e} = α \frac{0.09}{i / e} = 0.49 \frac{0.09}{6.41 / 10.39} = 0.636

Fórmula 33

O coeficiente de redução χ_c é determinado de acordo com [3] , 6.3.1.2 :

\begin{array}{l} ϕ = 0.5 \cdot (1.0 α_{e} \cdot ({\bar{λ}}_{c} - 0.2) {\bar{λ}}_{c}^{2}) = 0.5 \cdot (1.0 0.636 \cdot (0.443 - 0.2) 0 . 443^{2}) = 0.675 \\ χ_{c} = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}_{c}^{2}}} = \frac{1}{0.675 \sqrt{0 . 675^{2} - 0 . 443^{2}}} = 0.844 < 1 \end{array}

Fórmula 34

Interação entre encurvadura local e comportamento da laje.

O comportamento estrutural de todo o painel é determinado com o fator ξ, de acordo com [1] , Secção 4.5.4(1):

\begin{array}{l} ξ = \frac{σ_{cr, p}}{σ_{cr, c}} - 1 but 0 \leq ξ \leq 1 \\ ξ = \frac{95.9}{94.7} - 1 = 0.013 \end{array}

Fórmula 35

O coeficiente de redução final ρc é determinado com a equação de interação de acordo com [1] , Equação (4.13):

ρ_{c} = (ρ_{p} - χ_{c}) \cdot ξ \cdot (2 - ξ) + χ_{c} = (1 - 0, 844) \cdot 0, 013 \cdot (2 - 0, 013) + 0, 844 = 0, 848

Fórmula 36

Valores da secção efetiva

A superfície efetiva da zona de compressão A_c,ef do painel da placa reforçada é calculada de acordo com [1] , Equação (4.5):

A_{c, eff} = ρ_{c} \cdot A_{c, eff, loc, p} + \sum b_{edge, eff} \cdot t = 0, 848 \cdot 151, 6 24, 38 \cdot 1, 5 + 32, 54 \cdot 1, 5 = 214, 1 cm ²

Fórmula 37

A área de secção efetiva A_eff resulta em:

A_{eff} = A_{c, eff} + 2 \cdot b_{f} \cdot t_{f} = 214, 1 + 2 \cdot 80 \cdot 4 = 854, 1 cm ²

Fórmula 38

Secção equivalente devido à encurvadura local e global

Dimensionamento do painel reforçado

Os eixos do centro geométrico da secção bruta e da secção efetiva não coincidem, por isso atuam momentos de flexão adicionais devido ao deslocamento dos eixos do centro geométrico da secção efetiva relativos ao eixo central da secção bruta que tem de ser considerados aqui. Esses momentos de flexão adicionais são calculados da seguinte forma:

\begin{array}{l} e_{y} = 0.82 - 0.72 = 0.10 cm \\ e_{z} = 164.97 - 157.42 = 7.55 cm \\ M_{y} = N \cdot e_{z} = 4, 000 \cdot 7.55 = 30, 202.4 kNcm \\ M_{z} = N \cdot e_{y} = - 4, 000 \cdot 0.10 = - 414.3 kNcm \\ M_{u} = 30, 203.7 KNcm \\ M_{v} = - 306.4 KNcm \end{array}

Fórmula 39

A tensão máxima resulta em:

σ_{eff} = \frac{N}{A_{eff}} + \frac{M_{u} \cdot e_{v}}{I_{u, eff}} - \frac{M_{v} \cdot e_{u}}{I_{v, eff}} = \frac{4.000}{854, 1} + \frac{30.203, 7 \cdot 165, 12}{17.466.764} - \frac{- 306, 4 \cdot 40, 23}{352.626} = 5, 01 kN / cm ²

Fórmula 40

O dimensionamento é realizado de acordo com [1] , Equação (4.15) como se segue:

η_{1} = \frac{σ_{eff}}{\frac{f_{y}}{γ_{M 0}}} = \frac{5.01}{\frac{34.5}{1.0}} = 0.15

Fórmula 41

Dimensionamento da encurvadura por torção

De acordo com [1] , Secção 9.2.1(8) tem de ser cumprido o seguinte critério de forma geral para evitar a encurvadura por torção dos reforços com secções abertas:

\begin{array}{l} η_{1} = \frac{5, 3 \cdot f_{y} \cdot I_{p}}{E \cdot I_{S t . V e n}} \leq 1 \\ η_{1} = \frac{5, 3 \cdot 34, 5 \cdot 13.053}{21.000 \cdot 122} = 0, 93 \leq 1 \end{array}

Fórmula 42

I_p e I_St.Ven descrevem o momento de inércia polar e o momento de inércia de Saint-Venant da secção rígida só (sem placa), calculado em torno do ponto de ligação à placa.

Se é considerado o empenamento do reforço, a tensão de encurvadura por torção crítica_σcr tem de ser determinada primeiro. É calculada de acordo com [4] , Equação (2.119) e Equação (2.120) como se segue:

\begin{array}{l} σ_{cr 1} = \frac{1}{I_{p}} \cdot (\frac{π^{2} \cdot E \cdot I_{ω}}{l^{2}} + G \cdot I_{St . Ven}) für l < L_{cr} \\ σ_{cr 2} = \frac{1}{I_{p}} \cdot (2 \cdot \sqrt{C_{θ} \cdot E \cdot I_{ω}} + G \cdot I_{St . Ven}) für l > L_{cr} \end{array}

Fórmula 43

O reforço tem uma constante de empenamento de I_ω = 0 cm⁶. A tensão de encurvadura por torção crítica_σcr é simplificada para:

\begin{array}{l} σ_{cr 1} = σ_{cr 2} = \frac{1}{I_{p}} \cdot G \cdot I_{S t . V e n} \\ σ_{cr 1} = σ_{cr 2} = \frac{1}{13.053} \cdot 8.077 \cdot 122 = 75, 5 kN / cm ² \end{array}

Fórmula 44

I_p e I_St.Ven descrevem o momento de inércia polar e o momento de inércia de Saint-Venant da secção rígida só (sem placa), calculado em torno do ponto de ligação à placa.

De acordo com [1] , Secção 9.2.1(9), o critério em 9.2.1(8) ou o critério seguinte tem de ser considerado quando tem em consideração o empenamento do reforço:

\begin{array}{l} η_{2} = \frac{θ \cdot f_{y}}{σ_{cr 1}} \leq 1 \\ η_{3} = \frac{θ \cdot f_{y}}{σ_{cr 2}} \leq 1 \end{array}

Fórmula 45

Com um fator para assegurar o comportamento elástico de acordo com a secção da classe 3 de acordo com [5] de θ = 2 f para reforços com baixa rigidez ao empenamento (por exemplo, barra plana ou barra de aço com bolbo), o resultado é:

η_{2} = η_{3} = \frac{2 \cdot 34.5}{75.5} = 0.91 \leq 1

Fórmula 46

O dimensionamento à encurvadura por torção é assim cumprido.

SHAPE-THIN

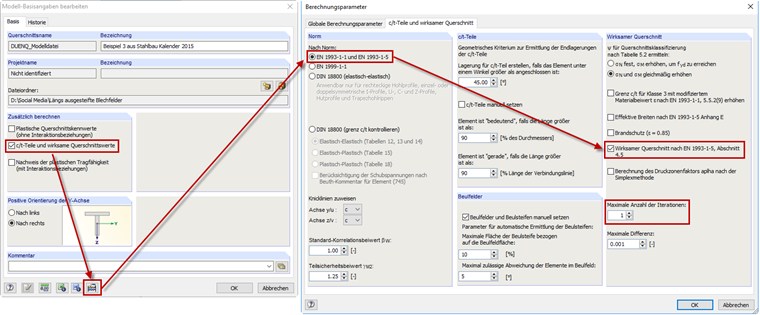
No SHAPE-THIN, é possível realizar o cálculo dos painéis reforçados longitudinalmente de acordo com [1] , Secção 4.5. O painel de controlo "partes c/t e propriedades da secção efetiva" tem de ser ativado nos dados gerais. Após, "EN 1993-1-1 e EN 1993-1-5" tem de ser selecionadas nos parâmetros de cálculo e o painel de controlo "secção efetiva de acordo com EN 1993-1-5, Secção 4.5" também tem de ser selecionada. A determinação das larguras efetivas deve ser realizada num processo iterativo de acordo com [1] , Secção 4.4(3). Neste exemplo, apenas uma iteração tem de ser utilizada para o cálculo, por isso também apenas uma iteração aparecerá no SHAPE-THIN (ver Figura 07).

Parâmetros de cálculo

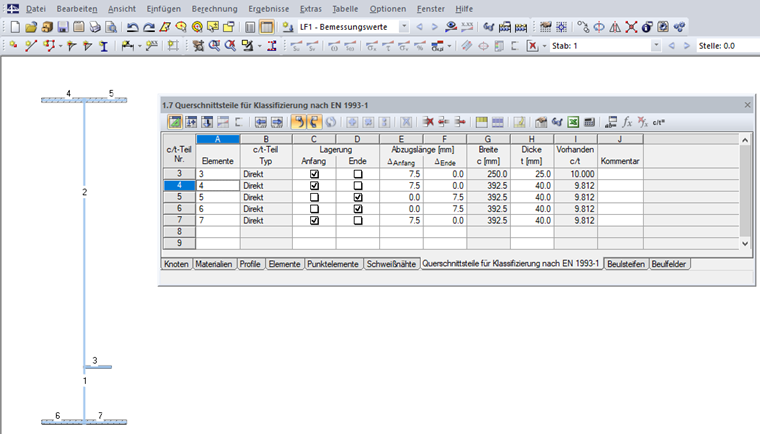
Os elementos da secção tem de ser introduzidos em primeiro lugar. As partes c/t são geralmente geradas automaticamente a partir das condições geométricas; contudo estas podem ser definidas pelo utilizador na Tabela "1.7 Partes de Secções para o cálculo de acordo com EN 1993-1" (ver Figura 08) ou a correspondente caixa e diálogo.

Partes da secção para classificação

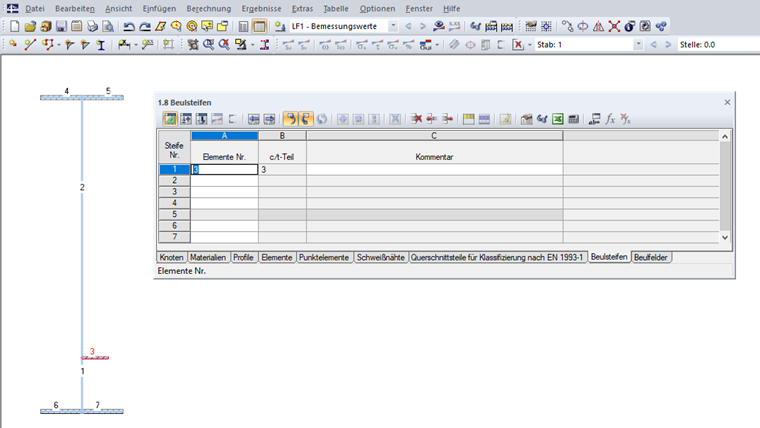
Os reforços podem depois ser definidos na Tabela "1.8 Reforço"ou na correspondente caixa de diálogo (ver Figura 09).

Reforços

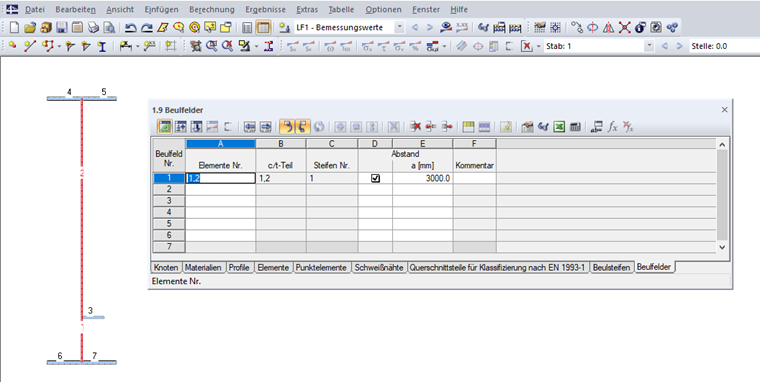
Além do mais, o painel reforçado tem de ser especificado na Tabela "1.9 painéis reforçados" (ver Figura 10) ou a correspondente caixa de diálogo. Os elementos do painel reforçado têm de ser selecionados e a distância do reforço transversal tem de ser introduzida. Se não for definida distância para o reforço transversal, o valor a = 10,000 mm será aplicado para o cálculo. Os reforços localizados no painel de encurvadura são identificados automaticamente. O painel reforçado tem de ser apoiado no seu inicio e final, o que significa que é necessário aqui um apoio.

Painéis reforçados

Os resultados da secção efetiva podem ser visualizados com o botão [Larguras efetivas].

Ergebnisse

Autor

A Eng.ª von Bloh fornece apoio técnico a clientes e também é responsável pelo desenvolvimento do programa RSECTION e pelas estruturas de aço e alumínio.

Ligações

Software para o dimensionamento de estruturas de aço

Referências

EC 3. (2009). Eurocódigo 3: Dimensionamento de estruturas de aço – Parte 1-5: Elementos estruturais constituídos por placas. Beuth GmbH.
Beg, D.; Kuhlmann, U.; Davaine, L.; & Braun, B. Dimensionamento de estruturas de placas. Eurocódigo 3: Dimensionamento de estruturas de aço. Parte 1-5 Dimensionamento de estruturas de placas. Berlin: Ernst & Sohn.
Kuhlmann, U. Stahlbau-Kalender 2015 - Eurocode 3 - Grundnorm, Leichtbau. Berlin: Ernst & Sohn, 2015
Johanson, B.; Maquoi, R.; Sedlacek, G.; Müller, C.; & Beg, D. Commentary and Worked Examples to EN 1993-1-5, Plated Structural Elements. Luxemburg: Office for Official Publications of the European Communities, 2007
EC 3. (2009). Eurocódigo 3: Eurocódigo 3: Dimensionamento de estruturas de aço – Parte 1-1: Regras gerais e regras para edifícios. (2010). Berlim: Beuth Verlag GmbH

Downloads

Ficheiro do modelo SHAPE-THIN

308 KB

;