7875x

001536

Sonja von Bloh, M.Sc.

12.9.2018

Podélně vyztužené části stěn podle EN 1993-1-5, článku 4.5

V programu SHAPE-THIN lze části stěn s podélnými výztuhami posoudit podle článku 4.5 normy EN 1993-1-5. U stěn s podélnými výztuhami se mají uvážit účinné plochy lokálního boulení různých subpanelů mezi výztuhami a účinné plochy celkového boulení vyztuženého panelu.

Nejdříve se stanoví účinné plochy jednotlivých polí pomocí redukčního součinitele podle EN 1993-1-5 [1] , čl. 4.4 pro zohlednění boulení jednotlivých polí. V druhém kroku se má posoudit vyztužená stěna s účinnými průřezy výztuh na celkové boulení při zohlednění prutového chování. Součinitelem celkového boulení se znovu redukují účinné šířky jednotlivých subpanelů. Dostaneme tak účinný průřez, který lze dále posuzovat jako průřez třídy 3.

Příklad použití

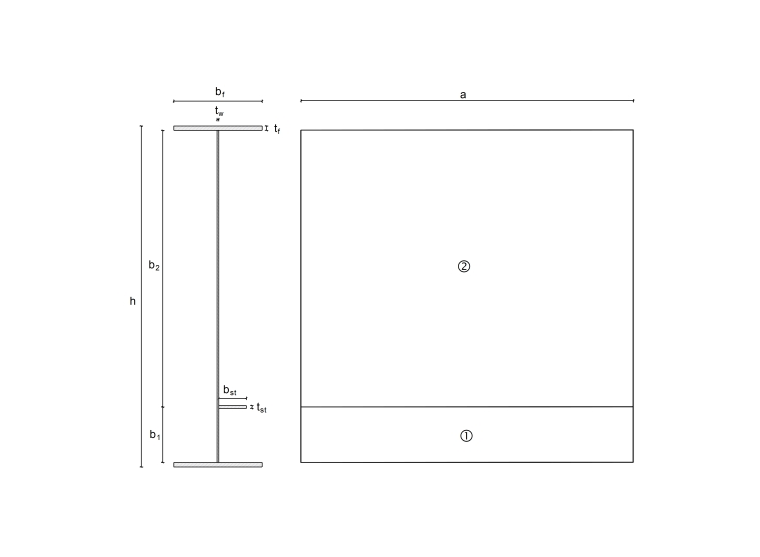
Následující příklad je převzat z Ročenky ocelových konstrukcí 2015 [2]. Průřez se skládá z I-nosníku, jehož stojina je vyztužena tuhými příčnými výztuhami a jednou podélnou výztuhou. Příčné výztuhy jsou umístěny ve vzdálenosti 3 m od sebe a podélná výztuha je přivařena 50 cm od dolní pásnice. Svary zanedbáme. Působí tlaková normálová síla N_Ed = 4 000 kN.

Průřez

Materiál:
S355 J0
f_y = 35,5 kN/cm² (pro t ≤ 3 mm a t ≤ 16 mm)
f_y = 34,5 kN/cm² (pro t >16 mm a t ≤ 40 mm)
E = 21000 kN/cm²
G = 8 076,92 kN/cm²
γ_M0 = 1,0

a = 3 000 mm
b₁ = 500 mm
b₂ = 2 500 mm
b_f = 800 mm
b_st = 250 mm
_tw = 15 mm
t_f = 40 mm
t_st = 25 mm
h = 3 080 mm

Plný průřez a rozdělení napětí

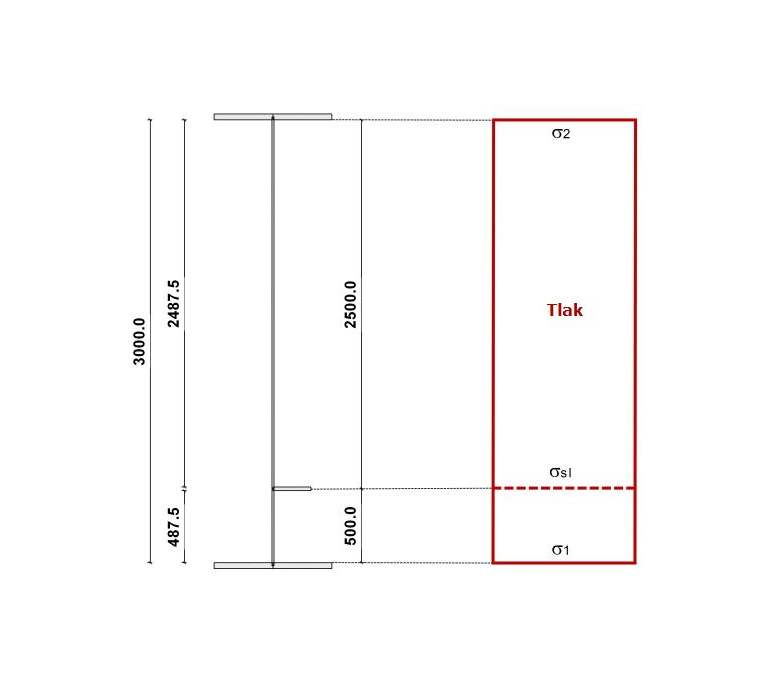
Napětí se vypočítá následovně:

σ_{1} = σ_{sl} = σ_{2} = \frac{N_{Ed}}{A} = \frac{4000}{1152, 5} = 3, 47 kN / cm ²

Vzorec 1

Plný průřez a rozdělení napětí jsou znázorněny na obr. 02.

průběh napětí

Klasifikace průřezů

Při klasifikaci průřezu se ověřuje, zda je nezbytné posoudit jednotlivé subpanely na boulení. Jestliže subpanely spadají alespoň do třídy průřezu 3, není lokální boulení rozhodující.

Pás

\begin{array}{l} c_{f} = \frac{b_{f} - t_{w}}{2} = \frac{800 - 15}{2} = 392, 5 mm \\ \frac{c_{f}}{t_{f}} = \frac{392, 5}{40} = 9, 8 \end{array}

Vzorec 2

Maximální poměr c/t λ_i se stanoví podle EN 1993-1-1 [3] , tabulky 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{c_{f}}{t_{f}} = 9, 8 \end{array}

Vzorec 3

Pásnici je třeba zařadit do třídy průřezu 3. Lokální boulení tak není rozhodující, a není tudíž nutné redukovat tento subpanel.

Stojina

\begin{array}{l} c_{1} = b_{1} - \frac{t_{st}}{2} = 500 - \frac{25}{2} = 487, 5 mm \\ \frac{c_{1}}{t_{w}} = \frac{487, 5}{15} = 32, 5 \end{array}

Vzorec 4

Maximální poměr c/t λ_i se stanoví podle [3] , tabulky 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 > \frac{c_{1}}{t_{w}} = 32, 5 \end{array}

Vzorec 5

Subpanel 1 se řadí do třídy průřezu 3. Lokální boulení tak není rozhodující, a není tudíž nutné redukovat tento subpanel.

\begin{array}{l} c_{2} = b_{2} - \frac{t_{st}}{2} = 2500 - \frac{25}{2} = 2487, 5 mm \\ \frac{c_{2}}{t_{w}} = \frac{2487, 5}{15} = 165, 8 \end{array}

Vzorec 6

Maximální poměr c/t λ_i se stanoví podle [3] , tabulky 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 < \frac{c_{2}}{t_{w}} = 165, 8 \end{array}

Vzorec 7

Subpanel 2 se řadí do třídy průřezu 4. U tohoto subpanelu je tak lokální boulení rozhodující a je třeba ho redukovat.

Koncová výztuha

\begin{array}{l} b_{st} = 250 mm \\ \frac{b_{st}}{t_{st}} = \frac{250}{25} = 10 \end{array}

Vzorec 8

Maximální poměr c/t λ_i se stanoví podle [3] , tabulky 5.2.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{b_{st}}{t_{st}} = 10 \end{array}

Vzorec 9

Stojina se řadí do třídy průřezu 3. Lokální boulení tak není rozhodující, a není tudíž nutné redukovat tento subpanel.

Účinné šířky

Subpanel 1 se řadí do třídy průřezu 3, takže lokální boulení není rozhodující. Účinné průřezové hodnoty tak odpovídají parametrům plného průřezu. Podle [1] , tabulky 4.1 z toho vyplývají následující účinné šířky:

\begin{array}{l} b_{1, eff} = c_{1} = 487, 5 mm \\ b_{1, edge, eff} = b_{1, edge} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \\ b_{1, \inf, eff} = b_{1, \inf} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \end{array}

Vzorec 10

Subpanel 2 je zařazen do třídy průřezu 4, a lokální boulení je tak rozhodující. Spolupůsobící šířky jednotlivé desky 2 se stanoví podle [1] , článku 4.4.

Napětí v subpanelu 2 má konstantní průběh. Z toho vyplývá využití ψ = 1 a podle tabulky 4.1 hodnota boulení k_σ = 4,0. Podle [1] , článku 4.4(2) je poměrná štíhlost λ_p2 :

${\bar{λ}}_{p 2} = \frac{\frac{c_{2}}{t_{w}}}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{165, 8}{28, 4 \cdot 0, 814 \cdot \sqrt{4}} = 3, 588$ Vzorec 12	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Vzorec 13
	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Vzorec 14

Součinitel lokální redukce ρ se stanoví podle [1] , rovnice (4.2):

ρ_{2} = \frac{{\bar{λ}}_{p 2} - 0, 055 \cdot (3 ψ)}{{\bar{λ}}_{p 2}^{2}} = \frac{3, 588 - 0, 055 \cdot (3 1)}{3, 588^{2}} = 0, 262 < 1

Vzorec 15

Účinné šířky prostého pole 2 se při zohlednění lokálního boulení stanoví podle [1] , tabulky 4.1:

\begin{array}{l} b_{2, eff} = ρ_{2} \cdot c_{2} = 0, 262 \cdot 2487, 5 = 650, 7 mm \\ b_{2, edge, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \\ b_{2, \sup, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \end{array}

Vzorec 16

Šířky plného průřezu se určí následovně:

\begin{array}{l} b_{2, edge} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2487, 5 = 1243, 8 mm \\ b_{2, \sup} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2487, 5 = 1243, 8 mm \end{array}

Vzorec 17

Stěnové chování

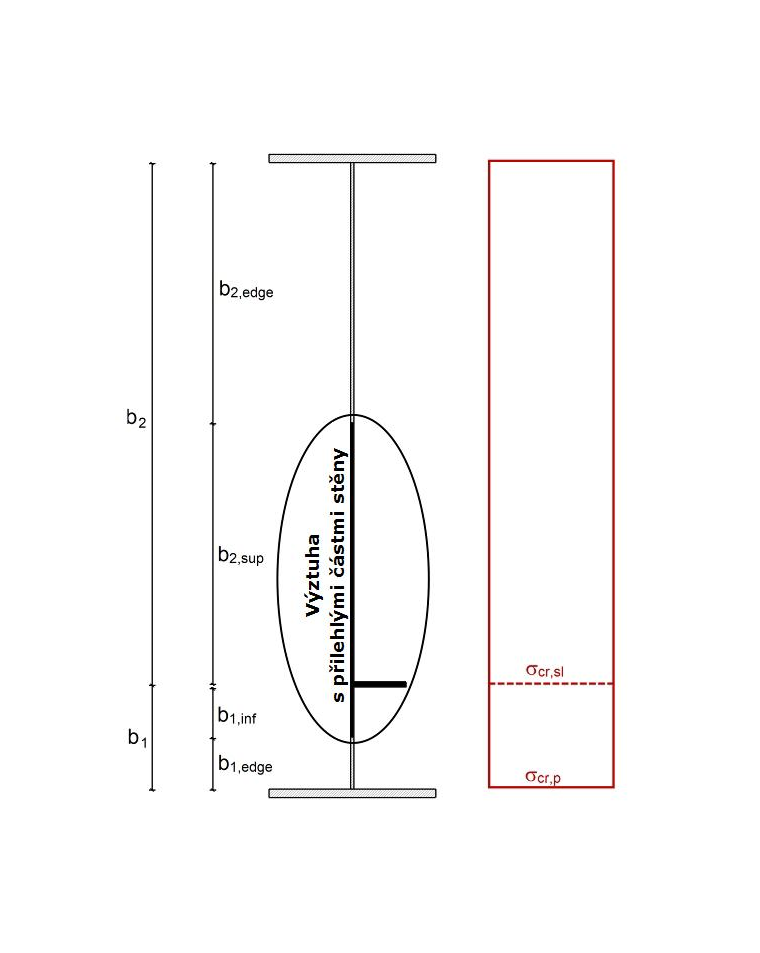
Pružné kritické napětí při boulení s tuhostí σcr,sl se stanoví podle [1] , přílohy A.2.2. Nejdříve je třeba spočítat vzpěrnou délku tuhosti a_c :

a_{c} = 4, 33 \cdot \sqrt[4]{\frac{I_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}}{t^{3} \cdot b}} = 4, 33 \cdot \sqrt[4]{\frac{11900 \cdot 50^{2} \cdot 250^{2}}{1, 5^{3} \cdot (50 250)}} = 896, 4 cm > a = 300 cm

Vzorec 18

Pružné kritické napětí při boulení s tuhostí σ_cr,sl je a < a_c v:

\begin{array}{l} σ_{cr, sl} = \frac{π^{2} \cdot E \cdot I_{sl, 1}}{A_{sl, 1} \cdot a^{2}} + \frac{E \cdot t^{3} \cdot b \cdot a^{2}}{4 \cdot π^{2} \cdot (1 - ν^{2}) \cdot A_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}} für a < a_{c} \\ σ_{cr, sl} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} + \frac{21.000 \cdot 1, 5^{3} \cdot (50 250) \cdot 300^{2}}{4 \cdot π^{2} \cdot (1 - 0, 3^{2}) \cdot 289, 4 \cdot 50^{2} \cdot 250^{2}} = 95, 9 kN / {cm}^{2} \end{array}

Vzorec 19

I_sl,1 a A_sl,1 zde představují moment setrvačnosti neoslabeného průřezu a celkovou plochu průřezu náhradního tlačeného prutu podle [1] ; A.2.1(2) pro boulení kolmo k rovině desky a b₁ a b₂ popisují vzdálenosti výztuh k podélným okrajům (b₁ + b₂ = b).

Průběh napětí je konstantní. Pružné napětí při boulení σ_cr,p tak odpovídá kritickému napětí při boulení σ_cr,sl.

σ_{cr, p} = σ_{cr, sl} = 95, 9 kN / {cm}^{2}

Vzorec 20

Plný průřez výztuhy s přilehlými částmi stěny

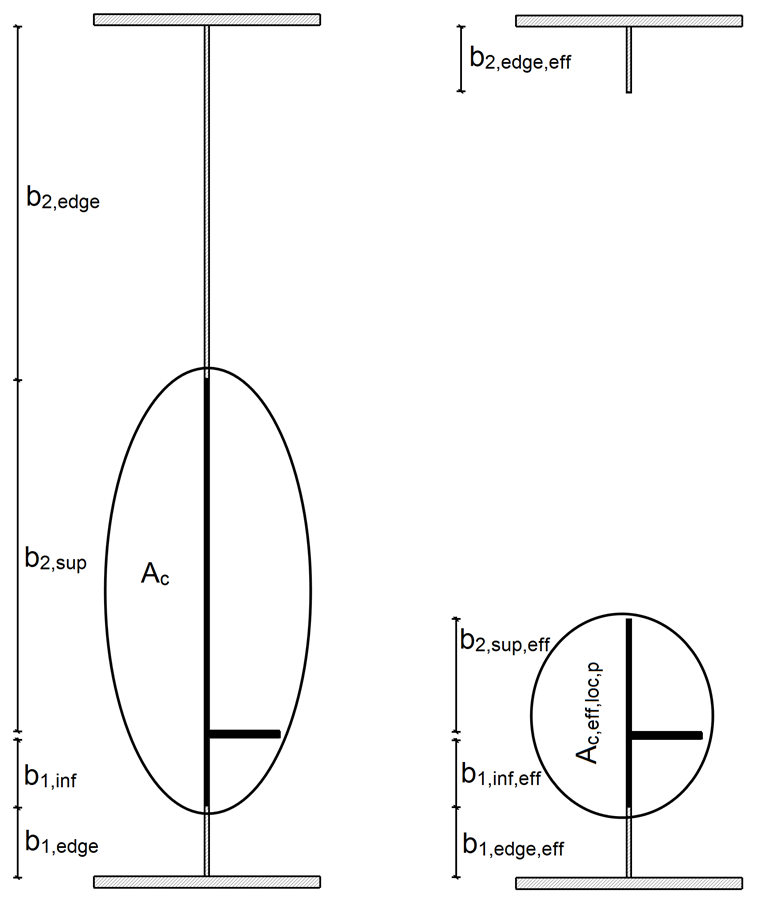
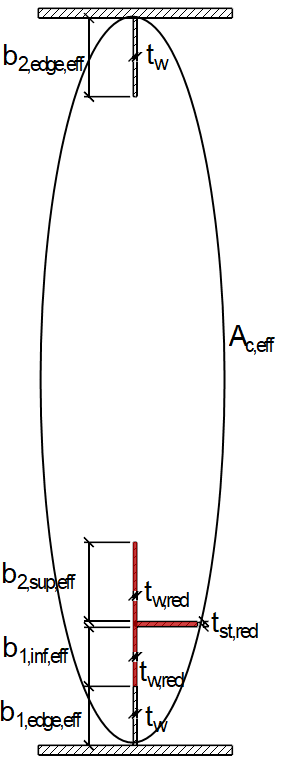
Hrubá průřezová plocha A_c podélně vyztuženého deskového panelu se vypočítá následovně, bez zohlednění okrajových desek podepřených sousedním deskovým prvkem a účinné plochy průřezu A_c,eff,loc,p plochy popsané výše:

A_{c} = (b_{1, \inf} + b_{2, \sup} + t_{st}) \cdot t_{w} + b_{st} \cdot t_{st} = (24, 38 + 124, 38 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 289, 4 {cm}^{2}

Vzorec 21

Výztuha patří do třídy průřezu 3, a tak účinná průřezová plocha výztuhy odpovídá ploše plného průřezu výztuhy.

A_{c, eff, loc, p} = (b_{1, \inf, eff} + b_{2, \sup, eff} + t_{st}) \cdot t_{w} + b_{st, eff} \cdot t_{st} = (24, 38 + 32, 54 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 151, 6 {cm}^{2}

Vzorec 22

Průřezové hodnoty jsou znázorněny na obr. 04.

Plný a účinný průřez lokálního boulení

Redukční součinitel β_a,c,p se stanoví podle [1] , článku 4.5.2 následovně:

\begin{array}{l} β_{a, c, p} = \frac{A_{c, eff, loc, p}}{A_{c}} \\ β_{a, c, p} = \frac{151, 6}{289, 4} = 0, 524 \end{array}

Vzorec 23

Globální štíhlost λ_p vyztužené desky podle [1] , rovnice (4.7):

${\bar{λ}}_{p} = \sqrt{\frac{β_{a, c, p} \cdot f_{y}}{σ_{cr, p}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{95, 9}} = 0, 440$ Vzorec 25	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Vzorec 26
	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Vzorec 27

Podle [1] , 4.4(2) je poměrná štíhlost λ_p menší než mezní hodnota 0,673. Proto není nutná redukce z důvodu chování desky; například ρ_p = 1,0.

Prutové chování

Pružné kritické napětí σ_cr,c se stanoví podle [1] , článku 4.5.3(3). Nejdříve se podle [1] , rovnice (4.9) stanoví vzpěrné napětí σ_cr,c,sl výztuhy, která se nachází na nejvíce zatíženém tlačeném okraji.

σ_{cr, c, sl} = \frac{π^{2} \cdot E \cdot I_{sl}}{A_{sl} \cdot a^{2}} = \frac{π^{2} \cdot 21000 \cdot 11900}{289, 4 \cdot 300^{2}} = 94, 7 kN / {cm}^{2}

Vzorec 28

Průběh napětí je konstantní. Pružné kritické napětí σ_cr,c tak odpovídá pružnému kritickému napětí σ_cr,c,sl výztuhy, která se nachází na maximálně zatíženém tlačeném okraji.

σ_cr,c = σ_cr,c,sl = 94,7 kN/cm²

Redukční součinitel β_a,c,c se stanoví podle [1] , článku 4.5.3(4) následovně:

β_{a, c, c} = \frac{A_{sl, eff}}{A_{sl}} = \frac{151, 6}{289, 4} = 0, 524

Vzorec 29

Poměrná štíhlost λcnáhradního tlačeného prutu podle [1] , rovnice (4.11):

{\bar{λ}}_{c} = \sqrt{\frac{β_{a, c, c} \cdot f_{y}}{σ_{cr, c}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{94, 7}} = 0, 443

Vzorec 31

Poloměr setrvačnosti i se vypočítá podle [1] , článku 4.5.3(5):

i = \sqrt{\frac{I_{sl}}{A_{sl}}} = \sqrt{\frac{11900}{289, 4}} = 6, 41 cm

Vzorec 32

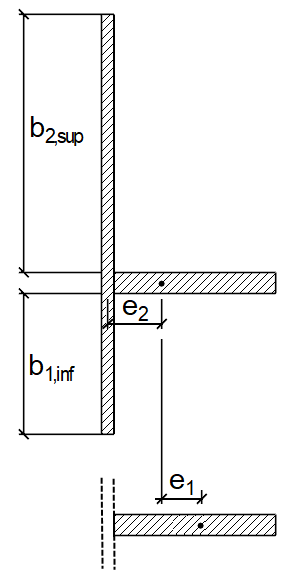
Vzdálenost e je větší z obou vzdáleností podle [1] , obrázku A.1; například buď vzdálenost e₁ jednotlivé výztuhy, upravená mezi těžištěm a uvažovaná nezávisle na desce, bez spolupůsobící šířky k těžišťové ose vyztuženého deskového panelu, nebo vzdálenost e₂ těžišťové osy vyztužené desky panelu ke střední rovině desky. Vzdálenosti jsou znázorněny na obrázku 05.

Ekvivalentní tlačený prut a výztuha: Vzdálenosti e1, e2

e = max (e₁, e₂ ) = max (10,39 cm, 2,86 cm) = 10,39 cm

Součinitel imperfekce αe se stanoví podle [1] , rovnice (4.12) s α = 0,49 pro otevřené průřezy výztuh následovně:

α_{e} = α \frac{0, 09}{i / e} = 0, 49 \frac{0, 09}{6, 41 / 10, 39} = 0, 636

Vzorec 33

Redukční součinitel χ_c se stanoví podle [3] , 6.3.1.2:

\begin{array}{l} ϕ = 0, 5 \cdot (1, 0 α_{e} \cdot ({\bar{λ}}_{c} - 0, 2) {\bar{λ}}_{c}^{2}) = 0, 5 \cdot (1, 0 0, 636 \cdot (0, 443 - 0, 2) 0, 443^{2}) = 0, 675 \\ χ_{c} = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}_{c}^{2}}} = \frac{1}{0, 675 \sqrt{0, 675^{2} - 0, 443^{2}}} = 0, 844 < 1 \end{array}

Vzorec 34

Interakce mezi stěnovým a prutovým chováním

Konstrukční chování celého panelu se stanoví pomocí součinitele ξ podle [1] , článku 4.5.4(1):

\begin{array}{l} ξ = \frac{σ_{cr, p}}{σ_{cr, c}} - 1 ovšem 0 \leq ξ \leq 1 \\ ξ = \frac{95, 9}{94, 7} - 1 = 0, 013 \end{array}

Vzorec 35

Konečný redukční součinitel ρc se stanoví pomocí interakční rovnice podle [1] , rovnice (4.13):

ρ_{c} = (ρ_{p} - χ_{c}) \cdot ξ \cdot (2 - ξ) + χ_{c} = (1 - 0, 844) \cdot 0, 013 \cdot (2 - 0, 013) + 0, 844 = 0, 848

Vzorec 36

Účinné průřezové parametry

Účinná plocha tlačené oblasti_Ac,eff vyztuženého deskového panelu se vypočítá podle [1] , rovnice (4.5):

A_{c, eff} = ρ_{c} \cdot A_{c, eff, loc, p} + \sum b_{edge, eff} \cdot t = 0, 848 \cdot 151, 6 24, 38 \cdot 1, 5 + 32, 54 \cdot 1, 5 = 214, 1 cm ²

Vzorec 37

Účinná průřezová plocha_Aeff je:

A_{eff} = A_{c, eff} + 2 \cdot b_{f} \cdot t_{f} = 214, 1 + 2 \cdot 80 \cdot 4 = 854, 1 cm ²

Vzorec 38

Účinný průřez lokálního a globálního boulení

Posouzení vyztužené stěny

Těžišťové osy plného a účinného průřezu se neshodují, a proto je třeba zohlednit přídavné ohybové momenty vlivem posunu těžišťové osy účinného průřezu vzhledem k těžišťové ose plného průřezu. Tyto přídavné ohybové momenty se vypočítají následovně:

\begin{array}{l} e_{y} = 0, 82 - 0, 72 = 0, 10 cm \\ e_{z} = 164, 97 - 157, 42 = 7, 55 cm \\ M_{y} = N \cdot e_{z} = 4000 \cdot 7, 55 = 30202, 4 kNcm \\ M_{z} = N \cdot e_{y} = - 4000 \cdot 0, 10 = - 414, 3 kNcm \\ M_{u} = 30203, 7 KNcm \\ M_{v} = - 306, 4 KNcm \end{array}

Vzorec 39

Maximální napětí je pak:

σ_{eff} = \frac{N}{A_{eff}} + \frac{M_{u} \cdot e_{v}}{I_{u, eff}} - \frac{M_{v} \cdot e_{u}}{I_{v, eff}} = \frac{4.000}{854, 1} + \frac{30.203, 7 \cdot 165, 12}{17.466.764} - \frac{- 306, 4 \cdot 40, 23}{352.626} = 5, 01 kN / cm ²

Vzorec 40

Posouzení se provádí podle [1] , rovnice (4.15) následovně:

η_{1} = \frac{σ_{eff}}{\frac{f_{y}}{γ_{M 0}}} = \frac{5, 01}{\frac{34, 5}{1, 0}} = 0, 15

Vzorec 41

Posouzení na vybočení zkroucením

Podle [1] , článku 9.2.1(8) musí být obecně splněno následující kritérium, aby se zabránilo vybočení výztuh s otevřeným průřezem:

\begin{array}{l} η_{1} = \frac{5, 3 \cdot f_{y} \cdot I_{p}}{E \cdot I_{S t . V e n}} \leq 1 \\ η_{1} = \frac{5, 3 \cdot 34, 5 \cdot 13.053}{21.000 \cdot 122} = 0, 93 \leq 1 \end{array}

Vzorec 42

I_p a I_St.Ven popisují polární moment setrvačnosti a St. Venantův moment setrvačnosti samotného průřezu s tuhostí (bez desky), počítané okolo bodu připojení k desce.

Při zohlednění deplanační tuhosti je třeba nejdříve stanovit kritické napětí při vzpěru σ_cr. Vypočítá se podle [4] , rovnice (2.119) a rovnice (2.120) následovně:

\begin{array}{l} σ_{cr 1} = \frac{1}{I_{p}} \cdot (\frac{π^{2} \cdot E \cdot I_{ω}}{l^{2}} + G \cdot I_{St . Ven}) für l < L_{cr} \\ σ_{cr 2} = \frac{1}{I_{p}} \cdot (2 \cdot \sqrt{C_{θ} \cdot E \cdot I_{ω}} + G \cdot I_{St . Ven}) für l > L_{cr} \end{array}

Vzorec 43

Tuhost má deplanační konstantu I_ω = 0 cm⁶. Kritické napětí při boulení σ_cr se tak zjednoduší na:

\begin{array}{l} σ_{cr 1} = σ_{cr 2} = \frac{1}{I_{p}} \cdot G \cdot I_{S t . V e n} \\ σ_{cr 1} = σ_{cr 2} = \frac{1}{13.053} \cdot 8.077 \cdot 122 = 75, 5 kN / cm ² \end{array}

Vzorec 44

I_p a I_St.Ven popisují polární moment setrvačnosti a St. Venantův moment setrvačnosti samotného průřezu s tuhostí (bez desky), počítané okolo bodu připojení k desce.

Podle [1] , článku 9.2.1(9) je třeba při zohlednění deplanační tuhosti obecně zohlednit kritérium v 9.2.1(8) nebo následující kritérium:

\begin{array}{l} η_{2} = \frac{θ \cdot f_{y}}{σ_{cr 1}} \leq 1 \\ η_{3} = \frac{θ \cdot f_{y}}{σ_{cr 2}} \leq 1 \end{array}

Vzorec 45

Se součinitelem θ = 2 f pro zajištění pružného chování podle třídy průřezu 3 podle [5] pro výztuhy s nízkou deplanační tuhostí (například plochá ocel nebo plochá ocel) se stanoví:

η_{2} = η_{3} = \frac{2 \cdot 34, 5}{75, 5} = 0, 91 \leq 1

Vzorec 46

Posouzení spolehlivosti proti vybočení zkroucením je tak splněno.

SHAPE-THIN

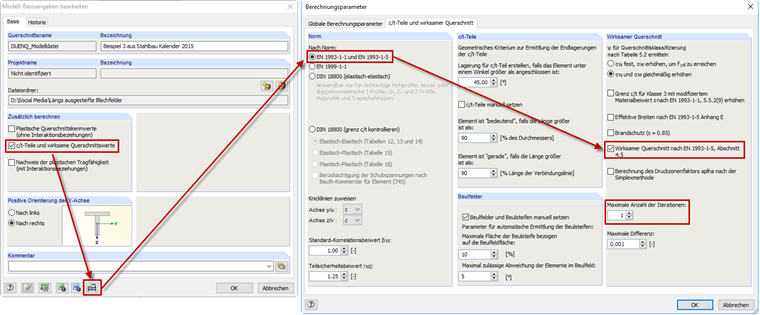
V programu SHAPE-THIN lze provést výpočet vyztužených polí boulení podle [1] , článku 4.5. V základních údajích je k tomu třeba označit políčko „c/t-části a účinné průřezové charakteristiky“. Následně musíme v parametrech výpočtu označit volbu „EN 1993-1-1 a EN 1993-1-5“ a dále „Spočítat účinný průřez podle části 4.5 Vyztužené části stěn s podélnými výztuhami“. Stanovení spolupůsobících šířek by mělo být provedeno iteračním postupem podle [1] , článku 4.4(3). Příklad jsme spočítali v jediné iteraci, a proto také v programu SHAPE-THIN nastavíme pouze jednu iteraci (viz obr. 07).

Parametry výpočtu

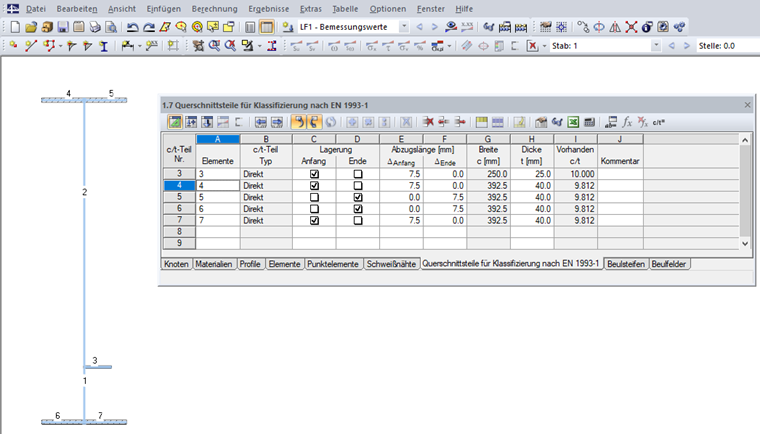
Nejdříve je třeba zadat prvky průřezu. c/t-části se zpravidla vytvoří automaticky na základě geometrických podmínek, uživatel je ovšem může také definovat v tabulce „1.7 Části průřezu pro klasifikaci podle EN 1993-1“ (viz obr. 08) anebo v příslušném dialogu.

Části průřezu pro klasifikaci

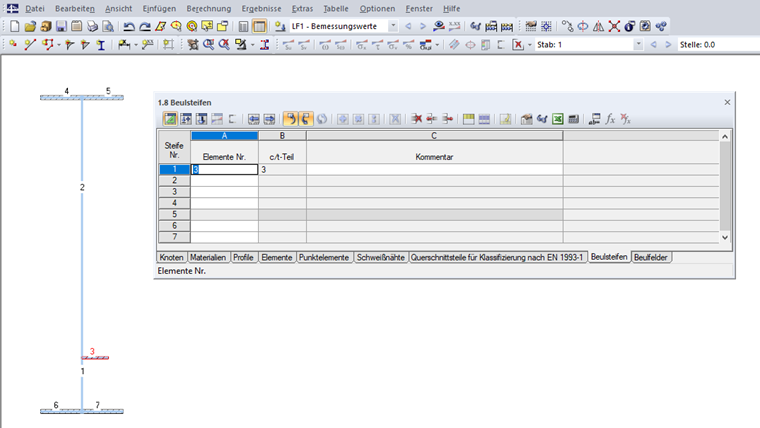
Výztuhy lze pak zadat v tabulce „1.8 Výztuhy“, případně v příslušném dialogu (viz obr. 09).

Výztuhy

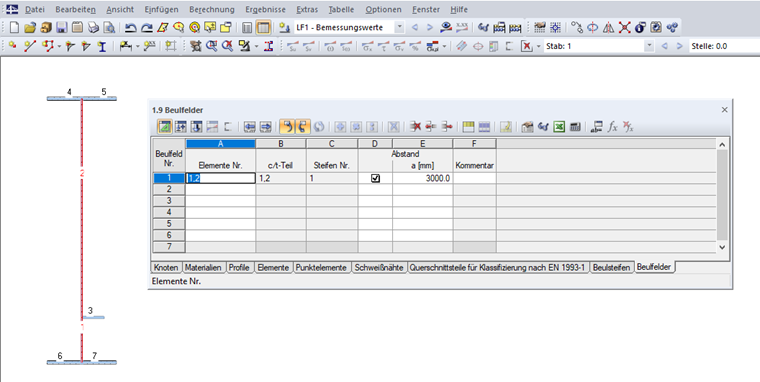
Dále je třeba zadat stěnu v tabulce „1.9 Vyztužené panely“ (viz obr. 10) anebo v příslušném dialogu. K tomu je třeba zadat prvky vyztuženého panelu a vzdálenost mezi příčnými výztuhami a. Pokud žádnou vzdálenost mezi příčnými výztuhami nezadáme, pak se bude při výpočtu uvažovat hodnota a = 10 000 mm. Výztuhy v panelu jsou rozpoznány automaticky. Vyztužený panel musí být podepřen na svém počátku i konci, čili musíme zadat příslušné podepření.

Panely

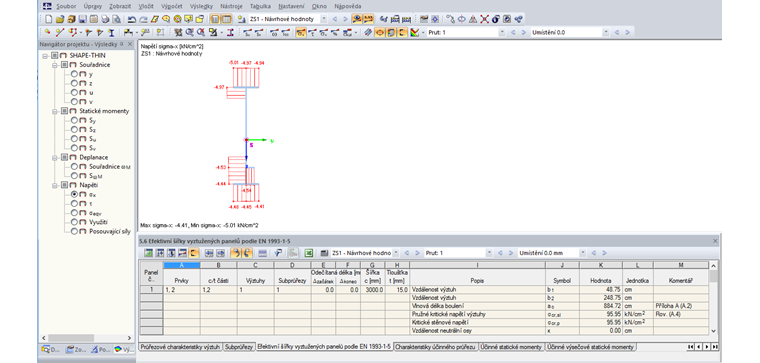
Výsledky účinného průřezu se nám zobrazí po kliknutí na tlačítko [Účinné šířky].

Ergebnisse

Autor

Ing. von Bloh zajišťuje technickou podporu zákazníkům a je zodpovědná za vývoj programu RSECTION a addonů pro ocelové a hliníkové konstrukce.

Odkazy

Software pro statické výpočty ocelových konstrukcí

Reference

Eurokód 3: Navrhování ocelových konstrukcí - Část 1-5: Oplechované konstrukční prvky. Nakladatelství Beuth GmbH.
Beg, D.; Kuhlmann, U.; Davaine, L.; & Braun, B. (2011). Návrh ocelových konstrukcí. Eurokód 3: Navrhování ocelových konstrukcí. Část 1-5 Navrhování deskových konstrukcí. Berlín: Ernst & Sohn, 2013
Kuhlmann, U.: (2015). Stahlbau-Kalender 2015 – Eurokód 3 – Grundnorm, Leichtbau. Berlín: Ernst & Sohn, 2013
Johannsson, B.; Maquoi, R.; Sedláček, G.; Müller, C.; & Beg, D. Commentary and Worked Examples to EN 1993-1-5, Plated Structural Elements. Luxemburg: Office for Official Publications of the European Communities, 2007
Eurokód 3: Bemessung und Konstruktion von Stahlbauten - Teil 1‑1: Obecná pravidla a pravidla pro pozemní stavby. (2010). Berlín: Beuth Verlag GmbH

Stahování

Model v programu SHAPE-THIN

308 KB

;