7857x

001536

Sonja von Bloh, M.Sc.

12. September 2018

Längs ausgesteifte Blechfelder gemäß EN 1993-1-5, Abschnitt 4.5

In DUENQ kann die Berechnung von längs ausgesteiften Blechfeldern gemäß Abschnitt 4.5 der EN 1993-1-5 erfolgen. Bei längs ausgesteiften Blechfeldern sind in der Regel sowohl die wirksamen Flächen infolge lokalen Beulens der Einzelfelder im Blech und in den Steifen als auch die wirksamen Flächen aus dem Gesamtfeldbeulen des ausgesteiften Gesamtfeldes zu berücksichtigen.

Es werden zunächst die wirksamen Flächen der Einzelfelder mit Hilfe des Abminderungsfaktors nach EN 1993-1-5 [1], Abschnitt 4.4 zur Berücksichtigung des Einzelfeldbeulens bestimmt. Im zweiten Schritt erfolgt die Ermittlung der Beulsicherheit des Gesamtfeldes unter Berücksichtigung des knickstabähnlichen Verhaltens. Mit dem Abminderungsfaktor des Gesamtfeldbeulens werden die effektiven Breiten der Einzelfelder erneut abgemindert. Man erhält so einen effektiven Querschnitt, welcher als Querschnitt der Querschnittsklasse 3 behandelt werden darf.

Beispiel

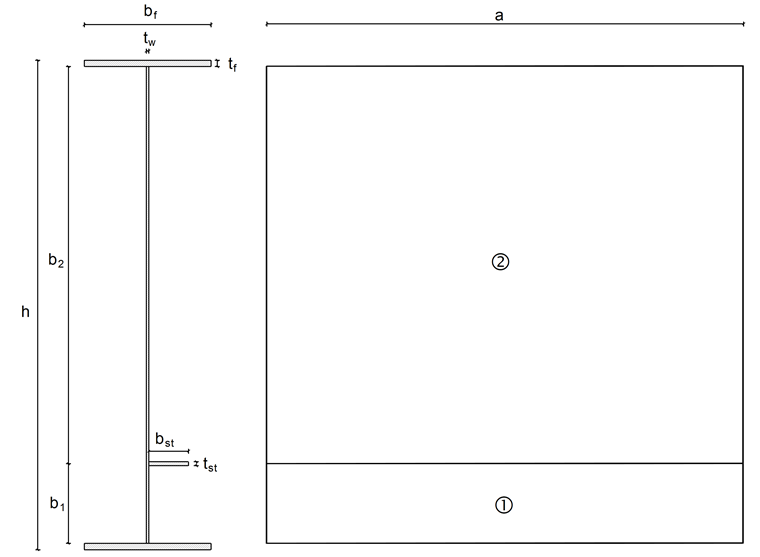
Das nachfolgende Beispiel ist dem Stahlbau Kalender 2015 [2] entnommen. Der Querschnitt besteht aus einem I-Träger, dessen Steg durch starre Quersteifen und einer Längssteife verstärkt ist. Die Quersteifen sind im Abstand von 3.000 mm zueinander positioniert und die Längssteife ist im Abstand von 500 mm vom unteren Flansch angeschweißt. Die Schweißnähte werden vernachlässigt. Es wirkt eine Drucknormalkraft von N_Ed = 4.000 kN.

Querschnitt

Material:
S355 J0
f_y = 35,5 kN/cm² (für t ≤ 3 mm und t ≤ 16 mm)
f_y = 34,5 kN/cm² (für t > 16 mm und t ≤ 40 mm)
E = 21.000 kN/cm²
G = 8.076,92 kN/cm²
γ_M0 = 1,0

a = 3.000 mm
b₁ = 500 mm
b₂ = 2.500 mm
b_f = 800 mm
b_st = 250 mm
t_w = 15 mm
t_f = 40 mm
t_st = 25 mm
h = 3.080 mm

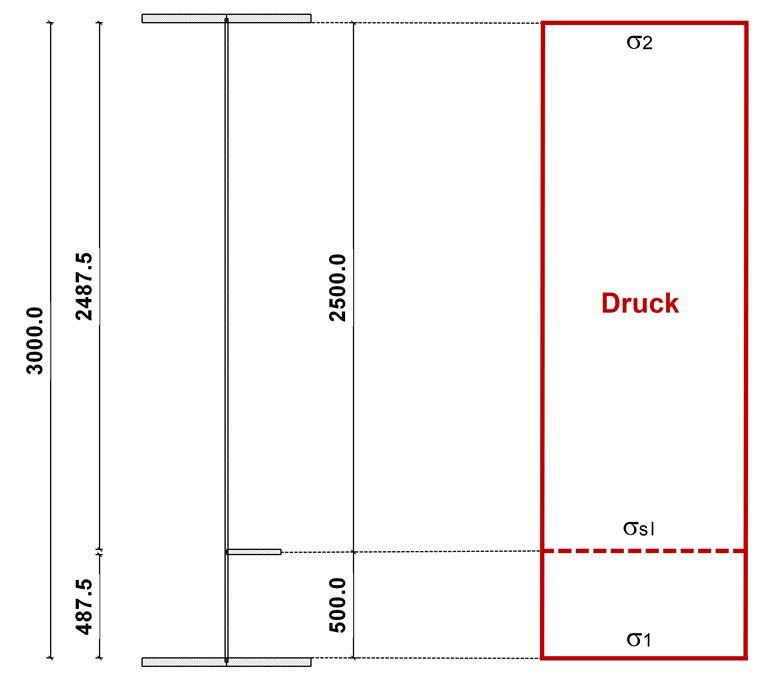
Bruttoquerschnitt und Spannungsverteilung

Die Spannung errechnet sich zu:

σ_{1} = σ_{sl} = σ_{2} = \frac{N_{Ed}}{A} = \frac{4.000}{1.152, 5} = 3, 47 kN / cm ²

Formel 1

Der Bruttoquerschnitt und die Spannungsverteilung sind in Bild 02 ersichtlich.

Spannungsverteilung

Querschnittsklassifizierung

Im Rahmen einer Querschnittsklassifizierung wird geprüft, ob für die Einzelfelder ein Beulnachweis erforderlich ist. Fällt das Einzelfeld zumindest in die Querschnittsklasse 3, ist lokales Beulen nicht maßgebend.

Flansch

\begin{array}{l} c_{f} = \frac{b_{f} - t_{w}}{2} = \frac{800 - 15}{2} = 392, 5 mm \\ \frac{c_{f}}{t_{f}} = \frac{392, 5}{40} = 9, 8 \end{array}

Formel 2

Das maximale c/t-Verhältnis λ_i wird gemäß EN 1993-1-1 [3], Tabelle 5.2 bestimmt.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{c_{f}}{t_{f}} = 9, 8 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{c_{f}}{t_{f}} = 9, 8 \end{array}

Formel 3

Der Flansch ist der Querschnittsklasse 3 zuzuordnen. Es ist somit kein lokales Beulen maßgebend und damit auch keine Abminderung der Einzelfelder des Flansches erforderlich.

Steg

\begin{array}{l} c_{1} = b_{1} - \frac{t_{st}}{2} = 500 - \frac{25}{2} = 487, 5 mm \\ \frac{c_{1}}{t_{w}} = \frac{487, 5}{15} = 32, 5 \end{array}

Formel 4

Das maximale c/t-Verhältnis λ_i wird gemäß [3], Tabelle 5.2 bestimmt.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{1}}{t_{w}} = 32, 5 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 > \frac{c_{1}}{t_{w}} = 32, 5 \end{array}

Formel 5

Das Einzelfeld 1 ist der Querschnittsklasse 3 zuzuordnen. Es ist somit kein lokales Beulen maßgebend und auch keine Abminderung dieses Einzelfeldes erforderlich.

\begin{array}{l} c_{2} = b_{2} - \frac{t_{st}}{2} = 2.500 - \frac{25}{2} = 2.487, 5 mm \\ \frac{c_{2}}{t_{w}} = \frac{2.487, 5}{15} = 165, 8 \end{array}

Formel 6

Das maximale c/t-Verhältnis λ_i wird gemäß [3], Tabelle 5.2 bestimmt.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0, 814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0, 814 = 26, 8 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0, 814 = 30, 9 < \frac{c_{2}}{t_{w}} = 165, 8 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0, 814 = 34, 2 < \frac{c_{2}}{t_{w}} = 165, 8 \end{array}

Formel 7

Das Einzelfeld 2 ist der Querschnittsklasse 4 zuzuordnen. Somit ist für dieses Einzelfeld lokales Beulen maßgebend und eine Abminderung des Einzelfeldes erforderlich.

Steife

\begin{array}{l} b_{st} = 250 mm \\ \frac{b_{st}}{t_{st}} = \frac{250}{25} = 10 \end{array}

Formel 8

Das maximale c/t-Verhältnis λ_i wird gemäß [3], Tabelle 5.2 bestimmt.

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0, 825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0, 825 = 7, 4 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0, 825 = 8, 2 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0, 825 = 11, 6 > \frac{b_{st}}{t_{st}} = 10 \end{array}

Formel 9

Der Steg ist der Querschnittsklasse 3 zuzuordnen. Es ist somit kein lokales Beulen maßgebend und damit auch keine Abminderung dieses Einzelfeldes erforderlich.

Effektive Breiten

Das Einzelfeld 1 ist der Querschnittsklasse 3 zugeordnet, sodass lokales Beulen nicht maßgebend ist. Damit entsprechen die effektiven Querschnittswerte den Bruttoquerschnittswerten. Gemäß [1], Tabelle 4.1 ergeben sich folgende wirksamen Breiten:

\begin{array}{l} b_{1, eff} = c_{1} = 487, 5 mm \\ b_{1, edge, eff} = b_{1, edge} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \\ b_{1, \inf, eff} = b_{1, \inf} = 0, 5 \cdot c_{1} = 0, 5 \cdot 487, 5 = 243, 8 mm \end{array}

Formel 10

Das Einzelfeld 2 ist der Querschnittsklasse 4 zugeordnet, sodass lokales Beulen maßgebend ist. Somit sind die effektiven Breiten des Einzelfeldes 2 gemäß [1], Abschnitt 4.4 zu bestimmen.

Die Spannungsverteilung im Einzelfeld 2 ist konstant. Somit ergibt sich ein Spannungsverhältnis ψ = 1 und gemäß Tabelle 4.1 ein Beulwert k_σ = 4,0. Damit ergibt sich für den Schlankheitsgrad λ_p2 nach [1], Abschnitt 4.4(2):

${\bar{λ}}_{p 2} = \frac{\frac{c_{2}}{t_{w}}}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{165, 8}{28, 4 \cdot 0, 814 \cdot \sqrt{4}} = 3, 588$ Formel 12	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Formel 13
	$> 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Formel 14

Der lokale Abminderungsfaktor ρ wird nach [1], Gleichung (4.2) ermittelt:

ρ_{2} = \frac{{\bar{λ}}_{p 2} - 0, 055 \cdot (3 ψ)}{{\bar{λ}}_{p 2}^{2}} = \frac{3, 588 - 0, 055 \cdot (3 1)}{3, 588^{2}} = 0, 262 < 1

Formel 15

Die effektiven Breiten des Einzelfeldes 2 unter Berücksichtigung des lokalen Beulens werden gemäß [1], Tabelle 4.1 berechnet:

\begin{array}{l} b_{2, eff} = ρ_{2} \cdot c_{2} = 0, 262 \cdot 2.487, 5 = 650, 7 mm \\ b_{2, edge, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \\ b_{2, \sup, eff} = 0, 5 \cdot b_{2, eff} = 0, 5 \cdot 650, 7 = 325, 4 mm \end{array}

Formel 16

Die Breiten des Bruttoquerschnittes ergeben sich zu:

\begin{array}{l} b_{2, edge} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \\ b_{2, \sup} = 0, 5 \cdot c_{2} = 0, 5 \cdot 2.487, 5 = 1.243, 8 mm \end{array}

Formel 17

Plattenartiges Verhalten

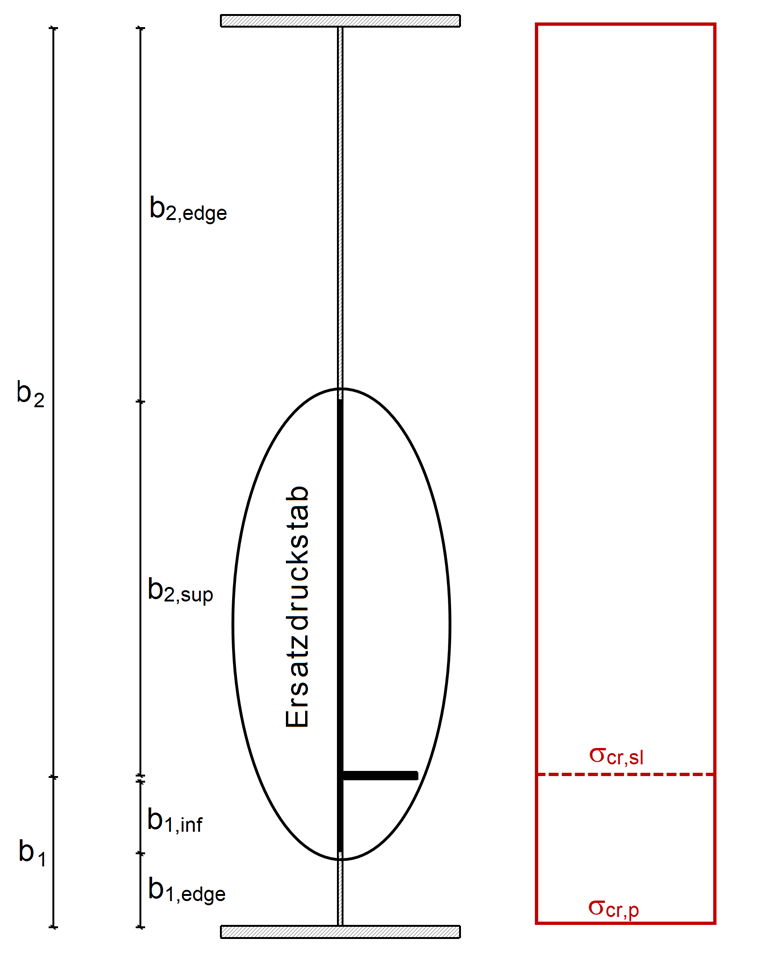
Die elastische kritische Knickspannung der Steife σ_cr,sl wird gemäß [1], Anhang A.2.2 berechnet. Es ist zunächst die Knicklänge der Steife a_c zu berechnen:

a_{c} = 4, 33 \cdot \sqrt[4]{\frac{I_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}}{t^{3} \cdot b}} = 4, 33 \cdot \sqrt[4]{\frac{11.900 \cdot 50^{2} \cdot 250^{2}}{1, 5^{3} \cdot (50 250)}} = 896, 4 cm > a = 300 cm

Formel 18

Die elastische kritische Knickspannung der Steife σ_cr,sl ergibt sich mit a < a_c zu:

\begin{array}{l} σ_{cr, sl} = \frac{π^{2} \cdot E \cdot I_{sl, 1}}{A_{sl, 1} \cdot a^{2}} + \frac{E \cdot t^{3} \cdot b \cdot a^{2}}{4 \cdot π^{2} \cdot (1 - ν^{2}) \cdot A_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}} für a < a_{c} \\ σ_{cr, sl} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} + \frac{21.000 \cdot 1, 5^{3} \cdot (50 250) \cdot 300^{2}}{4 \cdot π^{2} \cdot (1 - 0, 3^{2}) \cdot 289, 4 \cdot 50^{2} \cdot 250^{2}} = 95, 9 kN / {cm}^{2} \end{array}

Formel 19

Darin beschreiben I_sl,1 und A_sl,1 das Flächenträgheitsmoment des Bruttoquerschnitts und die Bruttoquerschnittsfläche des Ersatzdruckstabes nach [1], A.2.1(2) für Knicken quer zur Blechebene sowie b₁ und b₂ die Abstände der Steifen zu den Längsrändern (b₁ + b₂ = b).

Der Spannungsverlauf ist konstant. Daher entspricht die elastische Plattenbeulspannung σ_cr,p der elastischen kritischen Knickspannung σ_cr,sl.

σ_{cr, p} = σ_{cr, sl} = 95, 9 kN / {cm}^{2}

Formel 20

Bruttoquerschnitt Ersatzdruckstab

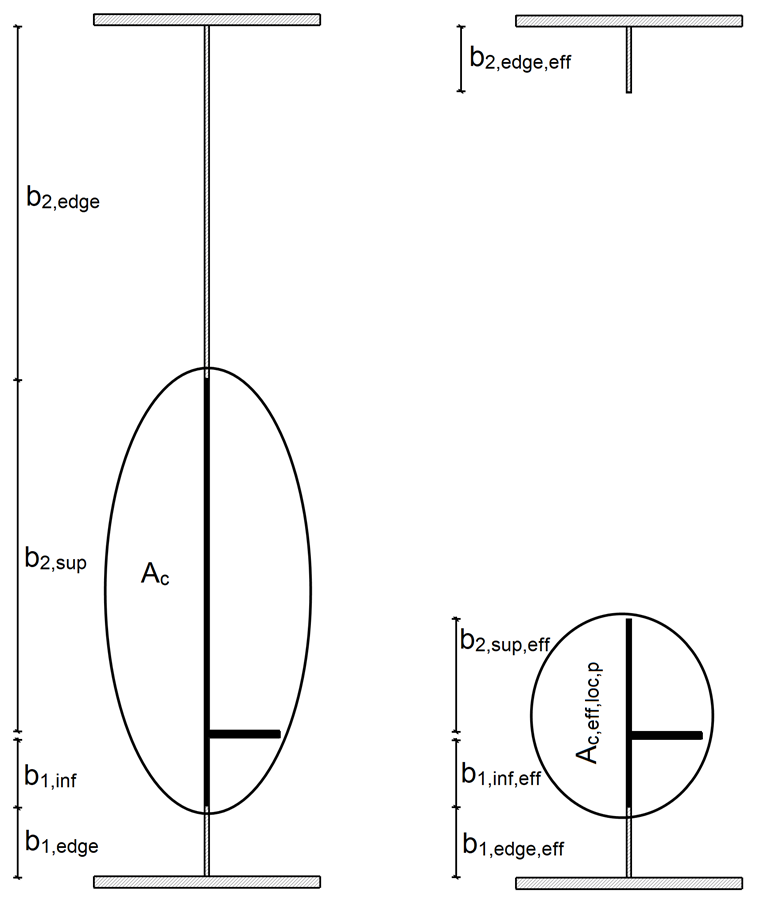
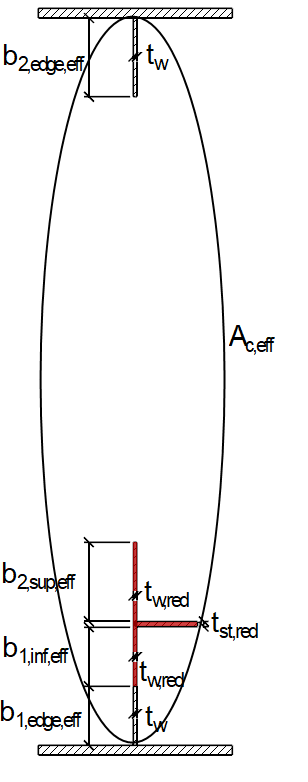
Die Bruttoquerschnittsfläche A_c des längs ausgesteiften Blechfeldes ohne Berücksichtigung der durch ein angrenzendes Plattenbauteil gestützten Randbleche und die effektive Querschnittsfläche A_c,eff,loc,p des zuvor beschriebenen Bereiches berechnen sich wie folgt:

A_{c} = (b_{1, \inf} + b_{2, \sup} + t_{st}) \cdot t_{w} + b_{st} \cdot t_{st} = (24, 38 + 124, 38 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 289, 4 {cm}^{2}

Formel 21

Die Steife fällt in die Querschnittsklasse 3, sodass die effektive Querschnittsfläche der Steife der Bruttoquerschnittsfläche der Steife entspricht.

A_{c, eff, loc, p} = (b_{1, \inf, eff} + b_{2, \sup, eff} + t_{st}) \cdot t_{w} + b_{st, eff} \cdot t_{st} = (24, 38 + 32, 54 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 151, 6 {cm}^{2}

Formel 22

Die Querschnittswerte sind in Bild 04 dargestellt.

Brutto- und effektiver Querschnitt infolge lokalen Beulens

Der Abminderungsfaktor β_a,c,p berechnet sich nach [1], Abschnitt 4.5.2 zu:

\begin{array}{l} β_{a, c, p} = \frac{A_{c, eff, loc, p}}{A_{c}} \\ β_{a, c, p} = \frac{151, 6}{289, 4} = 0, 524 \end{array}

Formel 23

Der globale Schlankheitsgrad λ_p der ausgesteiften Platte ergibt sich nach [1], Gleichung (4.7) zu:

${\bar{λ}}_{p} = \sqrt{\frac{β_{a, c, p} \cdot f_{y}}{σ_{cr, p}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{95, 9}} = 0, 440$ Formel 25	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ}$ Formel 26
	$< 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$ Formel 27

Der Schlankheitsgrad λ_p ist kleiner als der Grenzwert 0,673 nach [1], 4.4(2). Es ist somit keine Abminderung infolge plattenartigen Verhaltens notwendig, d. h. ρ_p = 1,0.

Knickstabähnliches Verhalten

Die elastische kritische Knickspannung σ_cr,c wird gemäß [1], Abschnitt 4.5.3(3) ermittelt. Es wird hierzu zunächst die Knickspannung σ_cr,c,sl der am höchstbelasteten Druckrand liegenden Steife nach [1], Gleichung (4.9) ermittelt:

σ_{cr, c, sl} = \frac{π^{2} \cdot E \cdot I_{sl}}{A_{sl} \cdot a^{2}} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} = 94, 7 kN / {cm}^{2}

Formel 28

Der Spannungsverlauf ist konstant. Daher entspricht die elastische kritische Knickspannung σ_cr,c der elastischen Knickspannung σ_cr,c,sl der am höchstbelasteten Druckrand liegenden Steife:

σ_cr,c = σ_cr,c,sl = 94,7 kN/cm²

Der Abminderungsfaktor β_a,c,cberechnet sich nach [1], Abschnitt 4.5.3(4) zu:

β_{a, c, c} = \frac{A_{sl, eff}}{A_{sl}} = \frac{151, 6}{289, 4} = 0, 524

Formel 29

Der Schlankheitsgrad λc des Ersatzdruckstabes ergibt sich nach [1], Gleichung (4.11) zu:

{\bar{λ}}_{c} = \sqrt{\frac{β_{a, c, c} \cdot f_{y}}{σ_{cr, c}}} = \sqrt{\frac{0, 524 \cdot 35, 5}{94, 7}} = 0, 443

Formel 31

Gemäß [1], Abschnitt 4.5.3(5) errechnet sich der Trägheitsradius i zu:

i = \sqrt{\frac{I_{sl}}{A_{sl}}} = \sqrt{\frac{11.900}{289, 4}} = 6, 41 cm

Formel 32

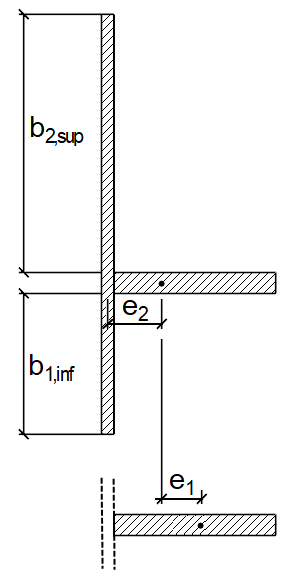
Der Abstand e ist der größere der beiden Abstände nach [1], Bild A.1, das heißt: entweder der Abstand e₁ zwischen dem Schwerpunkt der vom Blech isoliert betrachteten, angebrachten Einzelsteife ohne mitwirkende Breite zur Schwerachse des ausgesteiften Blechfeldes oder der Abstand e₂ der Schwerachse des ausgesteiften Blechfeldes zur Mittelebene des Bleches. Die Abstände sind in Bild 05 dargestellt.

Ersatzdruckstab und Steife: Abstände e1, e2

e = max (e₁, e₂) = max(10,39 cm, 2,86 cm) = 10,39 cm

Der Imperfektionsbeiwert α_e ermittelt sich gemäß [1], Gleichung (4.12) mit α = 0,49 für offene Steifenquerschnitte zu:

α_{e} = α \frac{0, 09}{i / e} = 0, 49 \frac{0, 09}{6, 41 / 10, 39} = 0, 636

Formel 33

Der Abminderungsfaktor χ_c wird nach [3], 6.3.1.2 bestimmt:

\begin{array}{l} ϕ = 0, 5 \cdot (1, 0 α_{e} \cdot ({\bar{λ}}_{c} - 0, 2) {\bar{λ}}_{c}^{2}) = 0, 5 \cdot (1, 0 0, 636 \cdot (0, 443 - 0, 2) 0, 443^{2}) = 0, 675 \\ χ_{c} = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}_{c}^{2}}} = \frac{1}{0, 675 \sqrt{0, 675^{2} - 0, 443^{2}}} = 0, 844 < 1 \end{array}

Formel 34

Interaktion zwischen knickstabähnlichem und plattenartigem Verhalten

Das Tragverhalten des Gesamtfeldes wird über den Beiwert ξ nach [1], Abschnitt 4.5.4(1) bestimmt:

\begin{array}{l} ξ = \frac{σ_{cr, p}}{σ_{cr, c}} - 1 jedoch 0 \leq ξ \leq 1 \\ ξ = \frac{95, 9}{94, 7} - 1 = 0, 013 \end{array}

Formel 35

Der endgültige Abminderungsfaktor ρ_c wird mit der Interaktionsgleichung nach [1], Gleichung (4.13) bestimmt:

ρ_{c} = (ρ_{p} - χ_{c}) \cdot ξ \cdot (2 - ξ) + χ_{c} = (1 - 0, 844) \cdot 0, 013 \cdot (2 - 0, 013) + 0, 844 = 0, 848

Formel 36

Effektive Querschnittswerte

Die wirksame Fläche der Druckzone A_c,eff des ausgesteiften Blechfeldes wird gemäß [1], Gleichung (4.5) berechnet:

A_{c, eff} = ρ_{c} \cdot A_{c, eff, loc, p} + \sum b_{edge, eff} \cdot t = 0, 848 \cdot 151, 6 24, 38 \cdot 1, 5 + 32, 54 \cdot 1, 5 = 214, 1 cm ²

Formel 37

Die effektive Querschnittsfläche A_eff ergibt sich zu:

A_{eff} = A_{c, eff} + 2 \cdot b_{f} \cdot t_{f} = 214, 1 + 2 \cdot 80 \cdot 4 = 854, 1 cm ²

Formel 38

Effektiver Querschnitt infolge lokalen und globalen Beulens

Nachweis des ausgesteiften Beulfeldes

Die Schwerachsen des Bruttoquerschnitts und des wirksamen Querschnitts fallen nicht zusammen, sodass hier zusätzliche einwirkende Biegemomente infolge der Verschiebung der Schwerachse des wirksamen Querschnitts bezogen auf die Schwerachse des Bruttoquerschnitts berücksichtigt werden müssen. Diese zusätzlichen Biegemomente berechnen sich zu:

\begin{array}{l} e_{y} = 0, 82 - 0, 72 = 0, 10 cm \\ e_{z} = 164, 97 - 157, 42 = 7, 55 cm \\ M_{y} = N \cdot e_{z} = 4.000 \cdot 7, 55 = 30.202, 4 kNcm \\ M_{z} = N \cdot e_{y} = - 4.000 \cdot 0, 10 = - 414, 3 kNcm \\ M_{u} = 30.203, 7 KNcm \\ M_{v} = - 306, 4 KNcm \end{array}

Formel 39

Die maximale Spannung ergibt sich zu:

σ_{eff} = \frac{N}{A_{eff}} + \frac{M_{u} \cdot e_{v}}{I_{u, eff}} - \frac{M_{v} \cdot e_{u}}{I_{v, eff}} = \frac{4.000}{854, 1} + \frac{30.203, 7 \cdot 165, 12}{17.466.764} - \frac{- 306, 4 \cdot 40, 23}{352.626} = 5, 01 kN / cm ²

Formel 40

Der Nachweis erfolgt nach [1], Gleichung (4.15) zu:

η_{1} = \frac{σ_{eff}}{\frac{f_{y}}{γ_{M 0}}} = \frac{5, 01}{\frac{34, 5}{1, 0}} = 0, 15

Formel 41

Nachweis der Drillknicksicherheit

Gemäß [1], Abschnitt 9.2.1(8) ist in der Regel das folgende Kriterium zu erfüllen, um Drillknicken von Steifen mit offenen Querschnitten zu vermeiden:

\begin{array}{l} η_{1} = \frac{5, 3 \cdot f_{y} \cdot I_{p}}{E \cdot I_{S t . V e n}} \leq 1 \\ η_{1} = \frac{5, 3 \cdot 34, 5 \cdot 13.053}{21.000 \cdot 122} = 0, 93 \leq 1 \end{array}

Formel 42

Darin bezeichnen I_p und I_St.Ven das polare Trägheitsmoment und Saint-Venantsche Torsionsträgheitsmoment des Steifenquerschnitts alleine (ohne Blech), gerechnet um den Anschlusspunkt an das Blech.

Wird die Wölbsteifigkeit berücksichtigt, ist zunächst die kritische Drillknickspannung σ_cr zu ermitteln. Diese berechnet sich nach [4], Gleichung (2.119) beziehungsweise Gleichung (2.120) wie folgt:

\begin{array}{l} σ_{cr 1} = \frac{1}{I_{p}} \cdot (\frac{π^{2} \cdot E \cdot I_{ω}}{l^{2}} + G \cdot I_{St . Ven}) für l < L_{cr} \\ σ_{cr 2} = \frac{1}{I_{p}} \cdot (2 \cdot \sqrt{C_{θ} \cdot E \cdot I_{ω}} + G \cdot I_{St . Ven}) für l > L_{cr} \end{array}

Formel 43

Die Steife hat einen Wölbwiderstand I_ω = 0 cm⁶. Die kritische Drillknickspannung σ_cr vereinfacht sich damit zu:

\begin{array}{l} σ_{cr 1} = σ_{cr 2} = \frac{1}{I_{p}} \cdot G \cdot I_{S t . V e n} \\ σ_{cr 1} = σ_{cr 2} = \frac{1}{13.053} \cdot 8.077 \cdot 122 = 75, 5 kN / cm ² \end{array}

Formel 44

Darin bezeichnen I_p und I_St.Ven das polare Trägheitsmoment und Saint-Venantsche Torsionsträgheitsmoment des Steifenquerschnitts alleine (ohne Blech), gerechnet um den Anschlusspunkt an das Blech.

Gemäß [1], Abschnitt 9.2.1(9) ist bei Berücksichtigung der Wölbsteifigkeit in der Regel das Kriterium in 9.2.1(8) oder das folgende Kriterium zu erfüllen:

\begin{array}{l} η_{2} = \frac{θ \cdot f_{y}}{σ_{cr 1}} \leq 1 \\ η_{3} = \frac{θ \cdot f_{y}}{σ_{cr 2}} \leq 1 \end{array}

Formel 45

Mit einem Beiwert zur Sicherstellung elastischen Verhaltens entsprechend der Querschnittsklasse 3 gemäß [5] von θ = 2 für Steifen mit geringer Wölbsteifigkeit (zum Beispiel Flachstahl oder Wulstflachstahl) ergibt sich:

η_{2} = η_{3} = \frac{2 \cdot 34, 5}{75, 5} = 0, 91 \leq 1

Formel 46

Der Nachweis der Drillknicksicherheit ist damit erbracht.

DUENQ

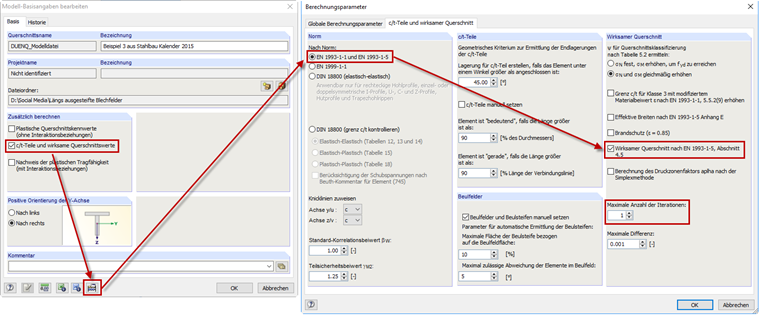
Die Berechnung von längs ausgesteiften Blechfeldern gemäß [1], Abschnitt 4.5 kann in DUENQ durchgeführt werden. In den Basisangaben ist dazu das Kontrollfeld "c/t-Teile und wirksame Querschnittswerte" zu aktivieren. Danach ist in den Berechnungsparametern "EN 1993-1-1 und EN 1993-1-5" auszuwählen sowie das Kontrollfeld "Wirksamer Querschnitt nach EN 1993-1-5, Abschnitt 4.5" anzuhaken. Die Ermittlung der wirksamen Breiten sollte gemäß [1], Abschnitt 4.4(3) in einem iterativen Prozess erfolgen. Im Beispiel wurde nur mit einer Iteration gerechnet, sodass auch in DUENQ nur eine Iteration eingestellt wird (siehe Bild 07).

Berechnungsparameter

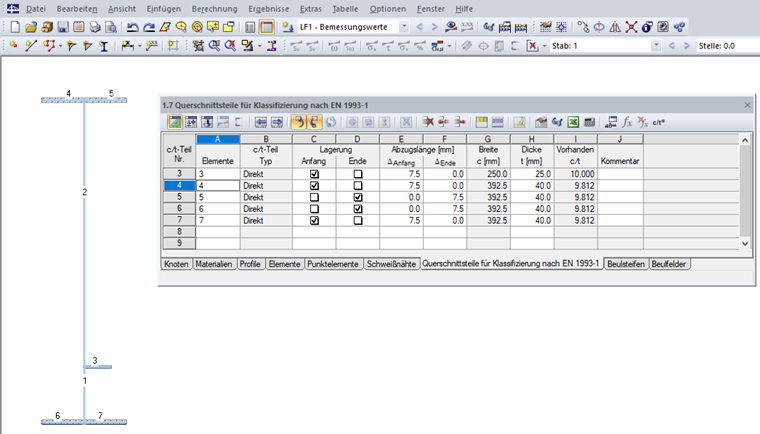
Es sind zunächst die Elemente des Querschnitts einzugeben. Die c/t-Teile werden in der Regel automatisch aus den Geometriebedingungen erzeugt, können aber auch benutzerdefiniert in Tabelle "1.7 Querschnittsteile für Klassifizierung nach EN 1993-1" (siehe Bild 08) oder dem entsprechenden Dialog angelegt werden.

Querschnittsteile für Klassifizierung

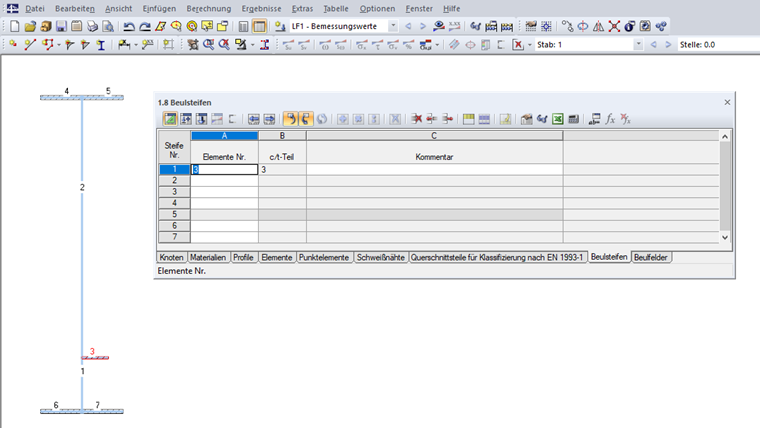
Die Beulsteifen können dann in der Tabelle "1.8 Beulsteifen" beziehungsweise dem entsprechenden Dialog definiert werden (siehe Bild 09).

Beulsteifen

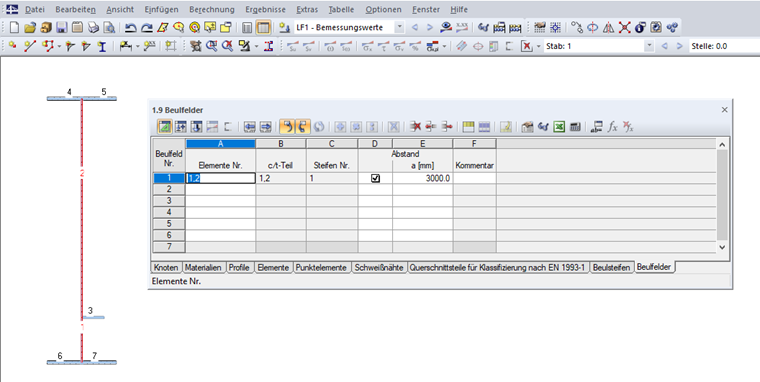
Des Weiteren ist das Beulfeld in Tabelle "1.9 Beulfelder" (siehe Bild 10) beziehungsweise dem entsprechenden Dialog anzugeben. Dazu sind die Elemente des Beulfelds auszuwählen und der Quersteifenabstand a einzugeben. Wird kein Quersteifenabstand definiert, so wird der Wert a = 10.000 mm für die Berechnung angesetzt. Die im Beulfeld liegenden Steifen werden automatisch erkannt. Das Beulfeld muss an seinem Anfang und Ende gestützt sein, also mit einer Lagerung versehen sein.

Beulfelder

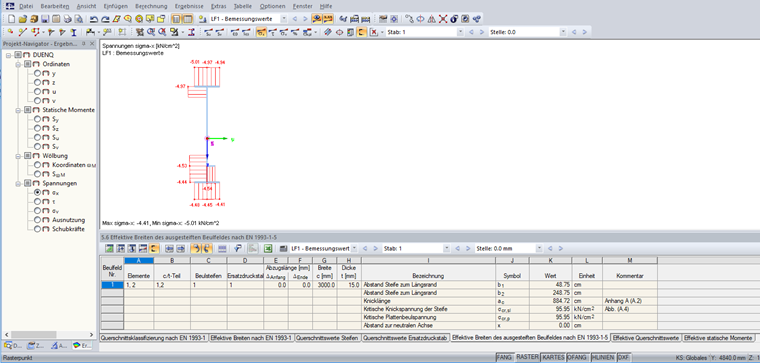
Die Ergebnisse des wirksamen Querschnitts sind mit der Schaltfläche [Effektive Breiten] zugänglich.

Ergebnisse

Autor

Frau von Bloh bietet im Kundensupport Hilfestellung für unsere Anwender und ist zudem für die Entwicklung des Programms RSECTION sowie für den Stahl- und Aluminiumbau zuständig.

Links

Statik-Software für Stahlbau

Referenzen

Eurocode 3: Bemessung und Konstruktion von Stahlbauten – Teil 1-5: Plattenförmige Bauteile. Beuth Verlag GmbH, Berlin, 2010.
Beg, D.; Kuhlmann, U.; Davaine, L.; Braun, B.: Design of Plated Structures. Eurocode 3: Design of Steel Structures. Part 1-5 Design of Plated Structures. Berlin: Ernst & Sohn, 2011
Kuhlmann, U.: Stahlbau-Kalender 2015 - Eurocode 3 - Grundnorm, Leichtbau. Berlin: Ernst & Sohn, 2015
Johansson, B.; Maquoi, R.; Sedlacek, G.; Müller, C.; Beg, D.: Commentary and Worked Examples to EN 1993-1-5, Plated Structural Elements. Luxemburg: Office for Official Publications of the European Communities, 2007
Eurocode 3: Bemessung und Konstruktion von Stahlbauten − Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010

Downloads

DUENQ-Modelldatei

308 KB

;