7881x

001536

Sonja von Bloh，硕士

2018-09-12

纵向加固钢板按照规范 EN 1993-1-5 章节 4.5

在软件 SHAPE-THIN 中计算纵向加固的钢板是按照规范 EN 1993-1-5 章节 4.5 进行。对于纵向加固的钢板，必须考虑由于在板中和加固件中的单个区域的局部屈曲得出的作用面积，还考虑由加固的整个区域的总区域屈曲得出的作用面积。

首先根据欧洲规范 EN 1993-1-5 [1]中章节 4.4 中的折减系数确定单个区域的屈曲度。第二步，考虑与屈曲杆件类似的屈曲行为来确定整个区域的屈曲安全性。使用整个区域屈曲的折减系数使得单个区域的有效宽度再次折减。这样得出的有效截面可以作为截面类型 3 处理。

示例

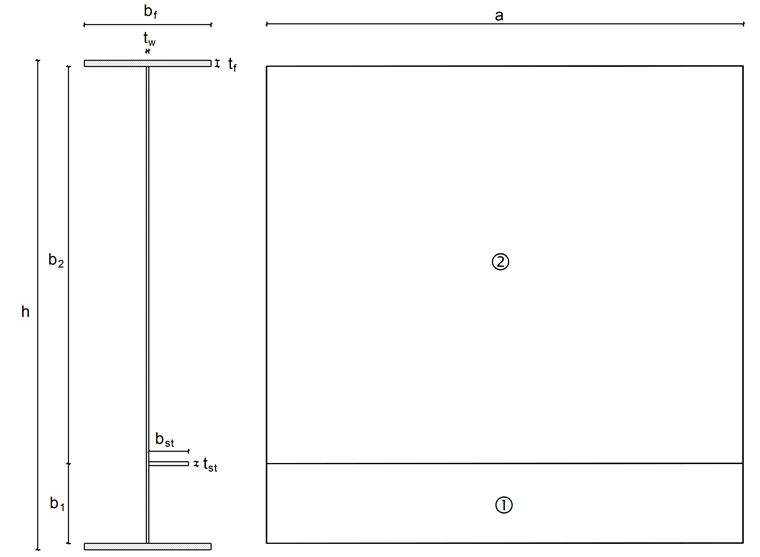
以下示例选自钢结构年鉴 2015 [2] 。截面是工字型，腹板在横向和纵向都被加固。横向加固之间的距离 3000 mm，纵向加固被焊接距离下翼缘 500 mm 处。焊缝忽略不计。作用的轴向压力为 N_Ed = 4.000 kN。

截面

材料:
S355 J0
f_y = 35.5 kN/cm² (当 t ≤ 3 mm 和 t ≤ 16 mm)
f_y = 34.5 kN/cm² (当 t >16 mm 和 t ≤ 40 mm)
E = 21 000 kN/cm²
G = 8076.92 kN/cm²
γ_M0 = 1.0

a = 3 000 mm
b₁ = 500mm
b₂ = 2.500 mm
b_f = 800mm
b_st = 250mm
t_w = 15mm
t_f = 40 mm
t_st = 25 mm
h = 3 080 mm

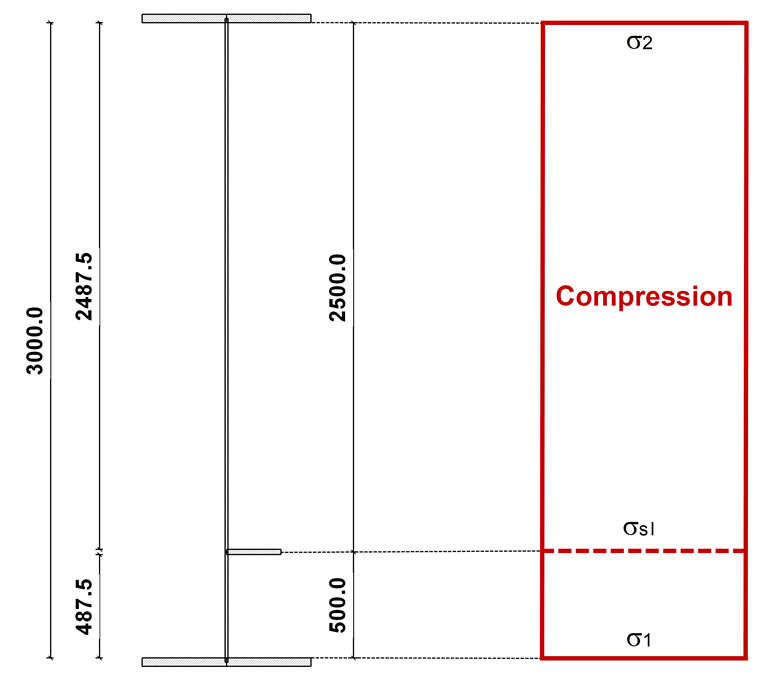
总截面和应力分布

应力计算如下：

σ_{1} = σ_{sl} = σ_{2} = \frac{N_{Ed}}{A} = \frac{4, 000}{1, 152.5} = 3.47 kN / cm ²

公式 1

总面积和应力分布如图 02 所示。

应力分布

截面分类

检查截面分类，确定是否要进行单个区域的屈曲验算。如果单个区域最少在截面分类 3 中，局部屈曲验算不起决定性作用。

弦杆

\begin{array}{l} c_{f} = \frac{b_{f} - t_{w}}{2} = \frac{800 - 15}{2} = 392.5 mm \\ \frac{c_{f}}{t_{f}} = \frac{392.5}{40} = 9.8 \end{array}

公式 2

最大 c/t 比值 λ_i是按照规范 EN 1993-1-1 [3]中表 5.2 计算。

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0.825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0.825 = 7.4 < \frac{c_{f}}{t_{f}} = 9.8 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0.825 = 8.2 < \frac{c_{f}}{t_{f}} = 9.8 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0.825 = 11.6 > \frac{c_{f}}{t_{f}} = 9.8 \end{array}

公式 3

翼缘归入截面分类 3。因此局部屈曲是不起决定性作用的，就不需要折减翼缘的单个区域。

腹板

\begin{array}{l} c_{1} = b_{1} - \frac{t_{st}}{2} = 500 - \frac{25}{2} = 487.5 mm \\ \frac{c_{1}}{t_{w}} = \frac{487.5}{15} = 32.5 \end{array}

公式 4

c/t 的最大比值 λ_i根据[3]中表 5.2 确定。

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0.814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0.814 = 26.8 < \frac{c_{1}}{t_{w}} = 32.5 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0.814 = 30.9 < \frac{c_{1}}{t_{w}} = 32.5 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0.814 = 34.2 > \frac{c_{1}}{t_{w}} = 32.5 \end{array}

公式 5

单个区域 1 归入截面分类 3。因此局部屈曲是不起决定性作用的，就不需要折减翼缘的单个区域。

\begin{array}{l} c_{2} = b_{2} - \frac{t_{st}}{2} = 2, 500 - \frac{25}{2} = 2, 487.5 mm \\ \frac{c_{2}}{t_{w}} = \frac{2, 487.5}{15} = 165.8 \end{array}

公式 6

c/t 的最大比值 λ_i根据[3]中表 5.2 确定。

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 355} = 0.814 \\ λ_{1} = 33 \cdot ε = 33 \cdot 0.814 = 26.8 < \frac{c_{2}}{t_{w}} = 165.8 \\ λ_{2} = 38 \cdot ε = 38 \cdot 0.814 = 30.9 < \frac{c_{2}}{t_{w}} = 165.8 \\ λ_{3} = 42 \cdot ε = 42 \cdot 0.814 = 34.2 < \frac{c_{2}}{t_{w}} = 165.8 \end{array}

公式 7

单个区域 2 归入截面分类 4。因此局部屈曲是起决定性作用的，还需要折减单个区域。

加劲肋

\begin{array}{l} b_{st} = 250 mm \\ \frac{b_{st}}{t_{st}} = \frac{250}{25} = 10 \end{array}

公式 8

c/t 的最大比值 λ_i根据[3]中表 5.2 确定。

\begin{array}{l} ε = \sqrt{235 / f_{y}} = \sqrt{235 / 345} = 0.825 \\ λ_{1} = 9 \cdot ε = 9 \cdot 0.825 = 7.4 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{2} = 10 \cdot ε = 10 \cdot 0.825 = 8.2 < \frac{b_{st}}{t_{st}} = 10 \\ λ_{3} = 14 \cdot ε = 14 \cdot 0.825 = 11.6 > \frac{b_{st}}{t_{st}} = 10 \end{array}

公式 9

腹板归入截面分类 3。因此局部屈曲不起决定性作用，就不需要折减翼缘的单个区域。

有效宽度

单个区域 1 归入截面分类 3，局部屈曲不起决定性作用。因此有效的截面属性与总截面属性相符合。根据[1]中表 4.1，得出以下有效宽度：

\begin{array}{l} b_{1, eff} = c_{1} = 487.5 mm \\ b_{1, edge, eff} = b_{1, edge} = 0.5 \cdot c_{1} = 0.5 \cdot 487.5 = 243.8 mm \\ b_{1, \inf, eff} = b_{1, \inf} = 0.5 \cdot c_{1} = 0.5 \cdot 487.5 = 243.8 mm \end{array}

公式 10

单个区域 2 归入截面分类 4，所以局部屈曲起决定性作用。单个区域 2 的有效宽度按照[1]中第 4.4 节计算。

在单个区域 2 中的应力分布是恒定的。由此得出应力比 ψ = 1 并且根据表 4.1 得出_σ k = 4,0 的屈曲系数。根据[1]中 4.4(2) 节，长细比 λ_p2为：

${\bar{λ}}_{p 2} = \frac{\frac{c_{2}}{t_{w}}}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{165.8}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 3.588$ 公式 12	$> 0.5 \sqrt{0.085 - 0.055 \cdot ψ}$ 公式 13
	$> 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673$ 公式 14

局部折减系数 ρ 根据[1]中公式（4.2）计算：

ρ_{2} = \frac{{\bar{λ}}_{p 2} - 0.055 \cdot (3 ψ)}{{\bar{λ}}_{p 2}^{2}} = \frac{3.588 - 0.055 \cdot (3 1)}{3 . 588^{2}} = 0.262 < 1

公式 15

区域 2 的有效宽度按照[1]中表 4.1 计算：

\begin{array}{l} b_{2, eff} = ρ_{2} \cdot c_{2} = 0.262 \cdot 2, 487.5 = 650.7 mm \\ b_{2, edge, eff} = 0.5 \cdot b_{2, eff} = 0.5 \cdot 650.7 = 325.4 mm \\ b_{2, \sup, eff} = 0.5 \cdot b_{2, eff} = 0.5 \cdot 650.7 = 325.4 mm \end{array}

公式 16

得出总截面的宽度：

\begin{array}{l} b_{2, edge} = 0.5 \cdot c_{2} = 0.5 \cdot 2, 487.5 = 1, 243.8 mm \\ b_{2, \sup} = 0.5 \cdot c_{2} = 0.5 \cdot 2, 487.5 = 1, 243.8 mm \end{array}

公式 17

板的性质

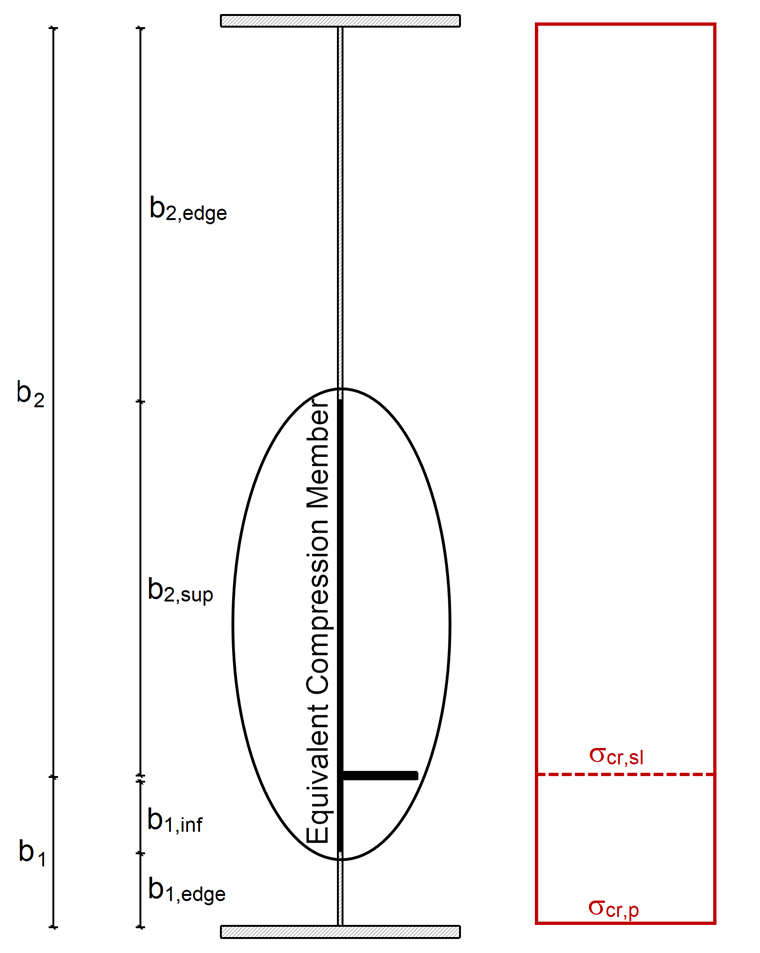
加固的弹性临界屈曲应力 σcr,sl 按照[1]中附录 A.2.2 计算。首先计算加劲肋的屈曲长度 a_c ：

a_{c} = 4.33 \cdot \sqrt[4]{\frac{I_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}}{t^{3} \cdot b}} = 4.33 \cdot \sqrt[4]{\frac{11, 900 \cdot 50^{2} \cdot 250^{2}}{1 . 5^{3} \cdot (50 250)}} = 896.4 cm > a = 300 cm

公式 18

σ_cr,sl的弹性临界屈曲应力 a < a_c ，

\begin{array}{l} σ_{cr, sl} = \frac{π^{2} \cdot E \cdot I_{sl, 1}}{A_{sl, 1} \cdot a^{2}} + \frac{E \cdot t^{3} \cdot b \cdot a^{2}}{4 \cdot π^{2} \cdot (1 - ν^{2}) \cdot A_{sl, 1} \cdot b_{1}^{2} \cdot b_{2}^{2}} für a < a_{c} \\ σ_{cr, sl} = \frac{π^{2} \cdot 21.000 \cdot 11.900}{289, 4 \cdot 300^{2}} + \frac{21.000 \cdot 1, 5^{3} \cdot (50 250) \cdot 300^{2}}{4 \cdot π^{2} \cdot (1 - 0, 3^{2}) \cdot 289, 4 \cdot 50^{2} \cdot 250^{2}} = 95, 9 kN / {cm}^{2} \end{array}

公式 19

I_sl,1和 A_sl,1表示毛截面惯性矩和按照[1]的等效受压构件的毛截面面积； A.2.1(2) 对于垂直于板平面的屈曲，b₁和 b₂为加劲肋到纵向边缘的距离 (b₁ + b₂ = b)。

应力分布是恒定的。因此，弹性的板屈曲应力 σ_cr,p与弹性临界屈曲应力 σ_cr,sl相一致。

σ_{cr, p} = σ_{cr, sl} = 95.9 kN / {cm}^{2}

公式 20

等效压杆总面积

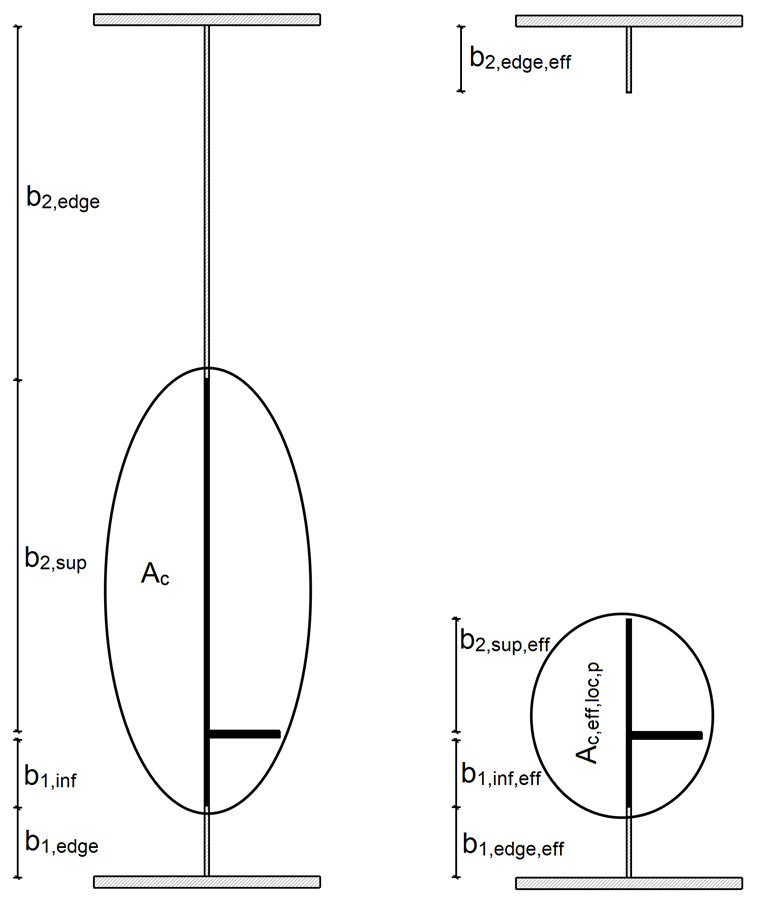
纵向加劲板格的总_截面积 A_c如下计算如上所述：

A_{c} = (b_{1, \inf} + b_{2, \sup} + t_{st}) \cdot t_{w} + b_{st} \cdot t_{st} = (24, 38 + 124, 38 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 289, 4 {cm}^{2}

公式 21

加固归入截面分类 3，加固的有效截面积与加固的总截面积相一致。

A_{c, eff, loc, p} = (b_{1, \inf, eff} + b_{2, \sup, eff} + t_{st}) \cdot t_{w} + b_{st, eff} \cdot t_{st} = (24, 38 + 32, 54 + 2, 5) \cdot 1, 5 + 25 \cdot 2, 5 = 151, 6 {cm}^{2}

公式 22

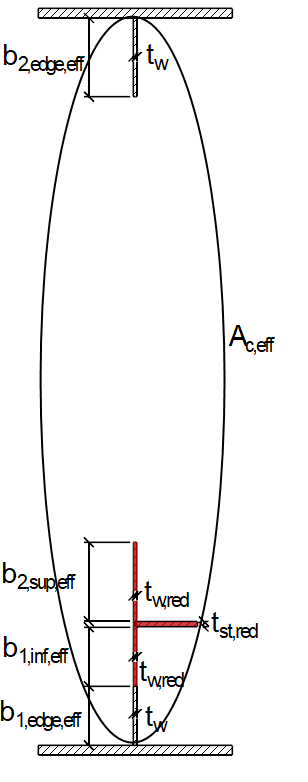
截面属性如图 04 所示。

总面积和有效面积由于局部屈曲

根据[1]中第 4.5.2 节，折减系数 β_a，c，p计算如下：

\begin{array}{l} β_{a, c, p} = \frac{A_{c, eff, loc, p}}{A_{c}} \\ β_{a, c, p} = \frac{151.6}{289.4} = 0.524 \end{array}

公式 23

根据[1]中公式（4.7），加劲板的总长细比 λ_p是：

${\bar{λ}}_{p} = \sqrt{\frac{β_{a, c, p} \cdot f_{y}}{σ_{cr, p}}} = \sqrt{\frac{0.524 \cdot 35.5}{95.9}} = 0.440$ 公式 25	$< 0.5 \sqrt{0.085 - 0.055 \cdot ψ}$ 公式 26
	$< 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673$ 公式 27

根据[1]中 4.4(2)，长细比 λ_p小于极限值 0.673。因此，不需要考虑板的性质进行折减；例如，ρ_p = 1.0。

类似屈曲杆件的性质

根据[1]中第 4.5.3(3) 节确定弹性临界屈曲应力 σ_cr,c 。首先，根据[1]中公式（4.9）确定最大受压边缘加劲肋的屈曲应力 σ_cr,c,sl 。

σ_{cr, c, sl} = \frac{π^{2} \cdot E \cdot I_{sl}}{A_{sl} \cdot a^{2}} = \frac{π^{2} \cdot 21, 000 \cdot 11, 900}{289.4 \cdot 300^{2}} = 94.7 kN / {cm}^{2}

公式 28

应力分布是恒定的。弹性临界屈曲应力 σ_cr,c和最大受压边缘的加固的弹性屈曲应力 σ_cr,c,sl相一致：

σ_cr,c = σ_cr,c,sl = 94.7 kN/cm²

根据[1]中第 4.5.3(4) 节，折减系数 β_a,c,c计算如下：

β_{a, c, c} = \frac{A_{sl, eff}}{A_{sl}} = \frac{151, 6}{289, 4} = 0, 524

公式 29

长细比 λC等效受压杆件结果，根据[1] ，公式 (4.11) 是：

{\bar{λ}}_{c} = \sqrt{\frac{β_{a, c, c} \cdot f_{y}}{σ_{cr, c}}} = \sqrt{\frac{0.524 \cdot 35.5}{94.7}} = 0.443

公式 31

根据[1]中 4.5.3(5) 节，回转半径 i 计算如下：

i = \sqrt{\frac{I_{sl}}{A_{sl}}} = \sqrt{\frac{11, 900}{289.4}} = 6.41 cm

公式 32

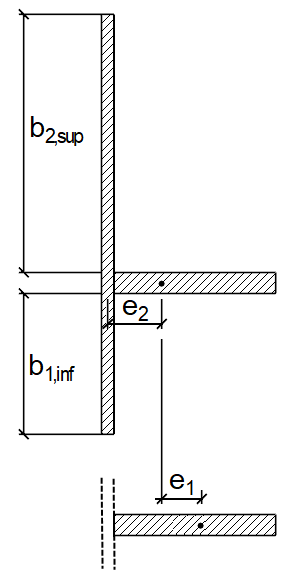
距离 e 根据[1]中图 A.1，取较大者；例如两者中一个加劲肋的距离 e₁ ，通过调整重心并且独立于板考虑，到加劲肋的重心轴没有有效宽度，或者是到加劲板重心轴的距离 e₂连接到板的中间平面。距离都在图 05 中显示。

等效受压杆件和加劲肋：距离e1，e2

e = max (e₁, e₂ ) = max(10.39 cm, 2.86 cm) = 10.39 cm

根据[1] ，公式（4.12）对于开口加劲截面，缺陷系数 αe 计算如下：

α_{e} = α \frac{0.09}{i / e} = 0.49 \frac{0.09}{6.41 / 10.39} = 0.636

公式 33

根据[3]中的 6.3.1.2 确定折减系数 x_c ：

\begin{array}{l} ϕ = 0.5 \cdot (1.0 α_{e} \cdot ({\bar{λ}}_{c} - 0.2) {\bar{λ}}_{c}^{2}) = 0.5 \cdot (1.0 0.636 \cdot (0.443 - 0.2) 0 . 443^{2}) = 0.675 \\ χ_{c} = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}_{c}^{2}}} = \frac{1}{0.675 \sqrt{0 . 675^{2} - 0 . 443^{2}}} = 0.844 < 1 \end{array}

公式 34

板的屈曲和板件行为之间的相互作用

根据[1]中第 4.5.4(1) 节，通过系数 ξ 确定整个区域的结构力学行为。

\begin{array}{l} ξ = \frac{σ_{cr, p}}{σ_{cr, c}} - 1 but 0 \leq ξ \leq 1 \\ ξ = \frac{95.9}{94.7} - 1 = 0.013 \end{array}

公式 35

最终折减系数 ρc 根据[1]中公式（4.13）确定：

ρ_{c} = (ρ_{p} - χ_{c}) \cdot ξ \cdot (2 - ξ) + χ_{c} = (1 - 0, 844) \cdot 0, 013 \cdot (2 - 0, 013) + 0, 844 = 0, 848

公式 36

有效截面属性

加劲肋板格受压区的有效面积 A_c,eff按照[1]中公式 (4.5) 计算：

A_{c, eff} = ρ_{c} \cdot A_{c, eff, loc, p} + \sum b_{edge, eff} \cdot t = 0, 848 \cdot 151, 6 24, 38 \cdot 1, 5 + 32, 54 \cdot 1, 5 = 214, 1 cm ²

公式 37

有效截面积 A_eff是：

A_{eff} = A_{c, eff} + 2 \cdot b_{f} \cdot t_{f} = 214, 1 + 2 \cdot 80 \cdot 4 = 854, 1 cm ²

公式 38

有效截面由于局部屈曲和整体屈曲

被加固钢板区域的设计计算

总截面的重心轴和有效截面的重心轴不重合，这里必须考虑由于两个重心轴相对偏移引起的附加作用的弯矩。计算附加弯矩：

\begin{array}{l} e_{y} = 0.82 - 0.72 = 0.10 cm \\ e_{z} = 164.97 - 157.42 = 7.55 cm \\ M_{y} = N \cdot e_{z} = 4, 000 \cdot 7.55 = 30, 202.4 kNcm \\ M_{z} = N \cdot e_{y} = - 4, 000 \cdot 0.10 = - 414.3 kNcm \\ M_{u} = 30, 203.7 KNcm \\ M_{v} = - 306.4 KNcm \end{array}

公式 39

得出的最大应力为：

σ_{eff} = \frac{N}{A_{eff}} + \frac{M_{u} \cdot e_{v}}{I_{u, eff}} - \frac{M_{v} \cdot e_{u}}{I_{v, eff}} = \frac{4.000}{854, 1} + \frac{30.203, 7 \cdot 165, 12}{17.466.764} - \frac{- 306, 4 \cdot 40, 23}{352.626} = 5, 01 kN / cm ²

公式 40

根据[1]中公式（4.15）：

η_{1} = \frac{σ_{eff}}{\frac{f_{y}}{γ_{M 0}}} = \frac{5.01}{\frac{34.5}{1.0}} = 0.15

公式 41

扭转屈曲验算

根据[1]中 9.2.1(8) ，为了避免开敞截面的加劲肋扭转屈曲，一般必须满足以下准则：

\begin{array}{l} η_{1} = \frac{5, 3 \cdot f_{y} \cdot I_{p}}{E \cdot I_{S t . V e n}} \leq 1 \\ η_{1} = \frac{5, 3 \cdot 34, 5 \cdot 13.053}{21.000 \cdot 122} = 0, 93 \leq 1 \end{array}

公式 42

加劲肋截面（无钢板）的极惯性矩 I_p和 I_St.Ven围绕与板的连接点计算。

考虑翘曲刚度，首先要计算临界扭转屈曲应力 σ_cr 。它根据[4]公式（2.119）和公式（2.120）计算如下：

\begin{array}{l} σ_{cr 1} = \frac{1}{I_{p}} \cdot (\frac{π^{2} \cdot E \cdot I_{ω}}{l^{2}} + G \cdot I_{St . Ven}) für l < L_{cr} \\ σ_{cr 2} = \frac{1}{I_{p}} \cdot (2 \cdot \sqrt{C_{θ} \cdot E \cdot I_{ω}} + G \cdot I_{St . Ven}) für l > L_{cr} \end{array}

公式 43

加劲肋的扇性模量 I_ω = 0 cm⁶ 。临界扭转屈曲应力 σ_cr简化为：

\begin{array}{l} σ_{cr 1} = σ_{cr 2} = \frac{1}{I_{p}} \cdot G \cdot I_{S t . V e n} \\ σ_{cr 1} = σ_{cr 2} = \frac{1}{13.053} \cdot 8.077 \cdot 122 = 75, 5 kN / cm ² \end{array}

公式 44

加劲肋截面（无钢板）的极惯性矩 I_p和 I_St.Ven围绕与板的连接点计算。

根据[1]中第 9.2.1(9) 条，在考虑翘曲刚度时，通常采用 9.2.1(8) 的验算：

\begin{array}{l} η_{2} = \frac{θ \cdot f_{y}}{σ_{cr 1}} \leq 1 \\ η_{3} = \frac{θ \cdot f_{y}}{σ_{cr 2}} \leq 1 \end{array}

公式 45

对于根据[5] θ = 2 f 的截面类别 3，对于具有低翘曲刚度的加劲肋（例如扁钢或球扁钢），确保弹性性能的系数为：

η_{2} = η_{3} = \frac{2 \cdot 34.5}{75.5} = 0.91 \leq 1

公式 46

因此实现了扭转屈曲安全性的设计计算。

SHAPE-THIN

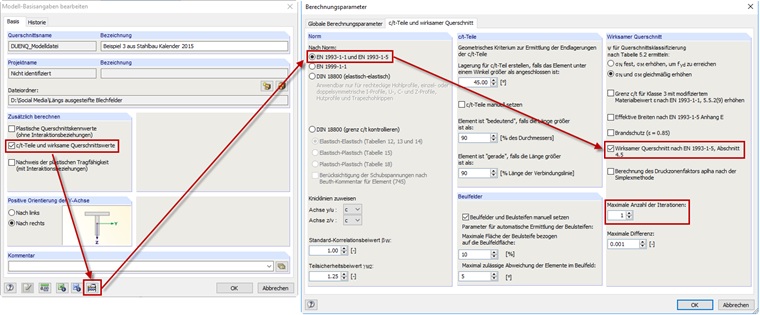
在 SHAPE-THIN 中计算纵向加固的屈曲板参见[1]中第 4.5 节。打开新建模型-基本数据的对话框时，激活附加计算区域的“c/t-比值和有效截面属性”。这样在计算参数中选择 "EN 1993-1-1 和 EN 1993-1-5"，以及在勾选附加计算区域的 "根据 EN 1993-1-5 中章节 4.5 计算有效截面" 。有效宽度的确定按照[1]中 4.4(3) 节在迭代过程中进行。在该例子中仅计算了一次迭代，因此在 SHAPE-THIN 中只要设置一次迭代（见图 07）。

计算参数

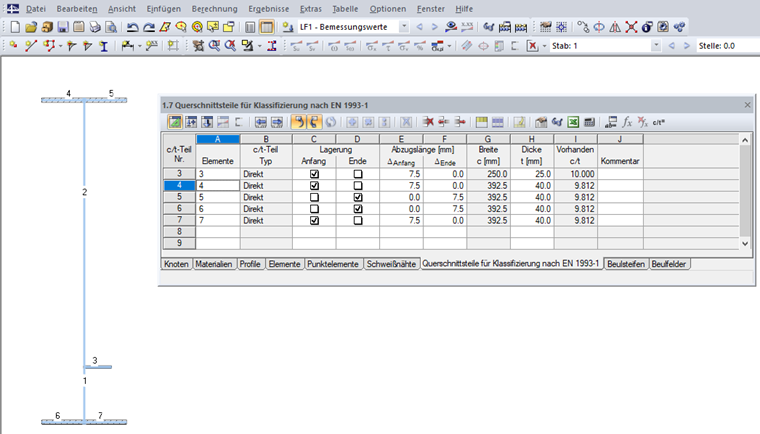
首先给出截面的单元。通常 c/t-比值是自动的通过几何条件创建，也能够在表格“1.7 截面部分按照 EN 1993-1 分类”（见图 08）或者在相应的对话框中由用户自定义。

截面部分分类

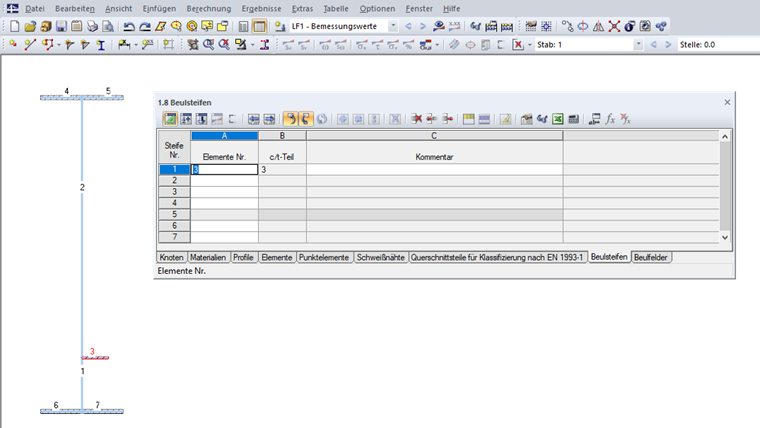
在表格“1.8 加劲肋”或者相应的对话框中定义加劲肋（见图 09）。

加劲肋

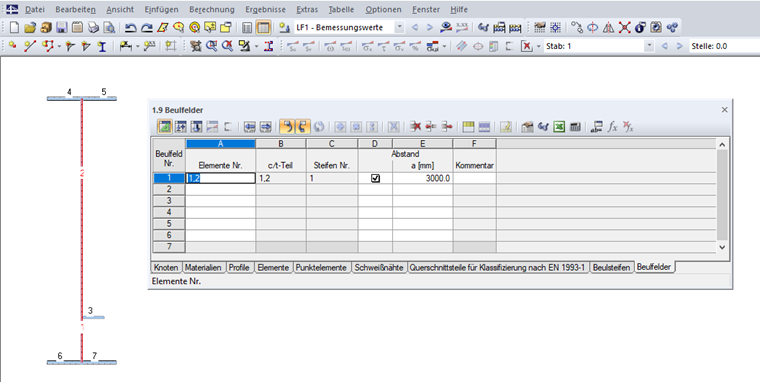
此外在表格“1.9 屈曲区域”（见图 10）或者相应的对话框中给出屈曲区域。为此要选择屈曲区域的单元以及给出横向加固距离 a。如果没有定义横向加固距离 a，那就对计算取值 a = 10 000 mm。程序会自动识别位于屈曲区域中的加劲肋。那么屈曲区域就会从头至尾的被加固，此外还装上支撑。

屈曲区域

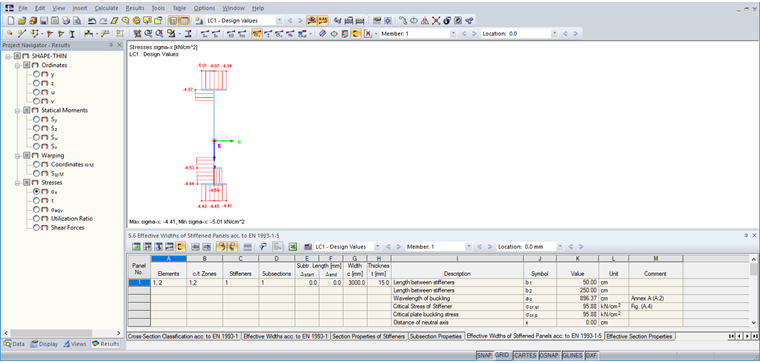
使用按钮 [有效宽度] 可以查看有效截面的结果。

Ergebnisse

作者

von Bloh 女士为我们的客户提供技术支持，负责 SHAPE-THIN 软件的开发，以及钢结构和铝合金结构的开发。

链接

钢结构分析软件

参考

EC 3.(2009)。欧洲规范 3：钢结构设计 - 第1-5部分：镀膜结构构件。 Beuth Publishing house GmbH。
Beg，D.；；Kuhlmann，U。 Ravaine, L.； & Braun, B. (2011)。板式结构设计。 EC 3.(2009)。欧洲规范 3：钢结构设计。板壳结构设计的第1-5部分。 Berlin: Ernst & Sohn。
库勒曼，U. Stahlbau-Kalender 2015 - Eurocode 3 - Grundnorm, Leichtbau. Berlin: Ernst & Sohn, 2015
Johansson, B.； Maquoi, R.； Sedlacek, G.； Müller，C。 &Beg, D. Commentary and Worked Examples to EN 1993-1-5, Plated Structural Elements. Luxemburg: Office for Official Publications of the European Communities, 2007
EC 3.(2009)。欧洲规范 3： 欧洲规范 3：钢结构设计 – 第 1-1 部分： 一般规范和建筑规范. (2010)。柏林：Beuth Verlag GmbH

下载

SHAPE-THIN 模型文件

308 KB

子面板屈曲加劲板屈曲

;