Методы решения уравнений в нелинейных расчетах

Введение

Метод конечных элементов обычно используется в тех случаях, когда задачи механики невозможно решить аналитически. При этом часто учитываются нелинейные эффекты, такие как выход из работы при сжатии (геометрическая нелинейность), пластификация (нелинейность материала) и контактные или кинематические степени свободы. Такие эффекты, особенно в случае применения нелинейной модели материала, можно учесть с помощью итерационного метода расчета.

Формулировка МКЭ

Основные этапы формулировки МКЭ (дальнейшая информация находится в {%ref#Refer [1]]]):

1. Слабая форма равновесия
   $${\int }_B\underset{nichtlinearer Anteil}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   δu	Virtuelle (Test-)Verschiebung
   t0	Anfangslastfaktor
   σdV	Innere Kräfte
   ρbdV	Volumenkräfte
   B	integriertes Gebiet

   Слабая форма
2. Преобразование в запись Фогта тензора 4й валентности
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Volumenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Oberflächenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	Steifigkeitsmatrix
   δε	Variation des Verzerrungszustands
   B	integriertes Gebiet
   ε	Dehnung
   u	Verformung

   Слабая форма в обозначениях Фойхта
3. На данной записи далее основывается приближенное решение МКЭ для нелинейных материалов,
4. причем поле смещения умножается на функции формы.
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u(x,t)	Verschiebung über Zeit (Lastinkrement)
   H	Formfunktion
   û	Knotenverschiebung

   Поле перемещения через пробную функцию

Использование производной смещения в слабой форме. Расчет перемещения узлов выполняется с помощью численного интегрирования, а постпроцессинге затем по закону материала определяется напряжения и деформации.

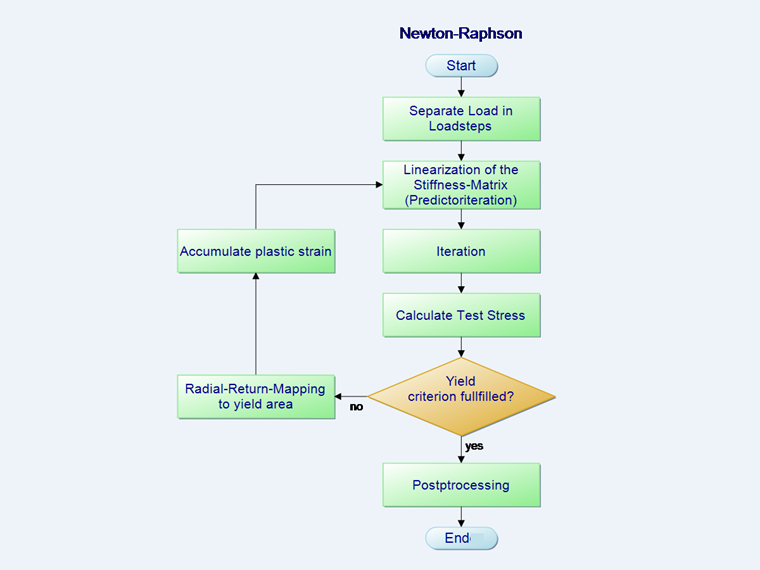
Порядок итерации Ньютона-Рафсона

Из-за нелинейных свойств материала матрица материала C в вышеприведенном равнении 2 меняется с каждым шагом деформации. Поэтому стандартным методом расчета для решения данной задачи является так называемая итерация Ньютона-Рафсона. При ее использовании функция линеаризируется уже в исходной точке. При итерации затем всегда используется матрица жесткости C из предыдущего шага. Только в линеаризованном шаге итерации проходит касательная через нулевую точку функции.

К схеме порядка итерации, которая показана на вышеприведенном рисунке, относятся также следующие уравнения:

1. Разделение нагружения на отдельные шаги нагрузки.
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fext	Äußere Last
   t	Zeit/Lastschritt
   Δf	Neues Lastinkrement

   Нагрузка в отдельных шагах нагрузки
2. Шаг предсказывания
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	Steifigkeitsmatrix des vorherigen Zeitschritts
   t+Δtfext	Äußere Kräfte um eine weitere Laststufe erhöht
   0tfint	Innere Kräfte des vorherigen Zeitschritts
   ϕ	Verzerrung

   Шаг предсказывания
3. В точке 3 - Итерации логической схемы рассчитывается общая деформация с вычетом пластической деформации (шаг коррекции). Главной целью итерационного расчета всегда является достижение условия, при котором сумма нагрузок равна нулю, но в числовом виде это невозможно. Поэтому задается предел прерывания ε, при достижениее которого будет расчет прерван как достаточно точный.
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   R	Abbruchrate
   fext	äußere Kräfte
   fint	innere Kräfte
   ε	Epsilon Abbruchrate
   t	Zeitschritt

   Предел отказа

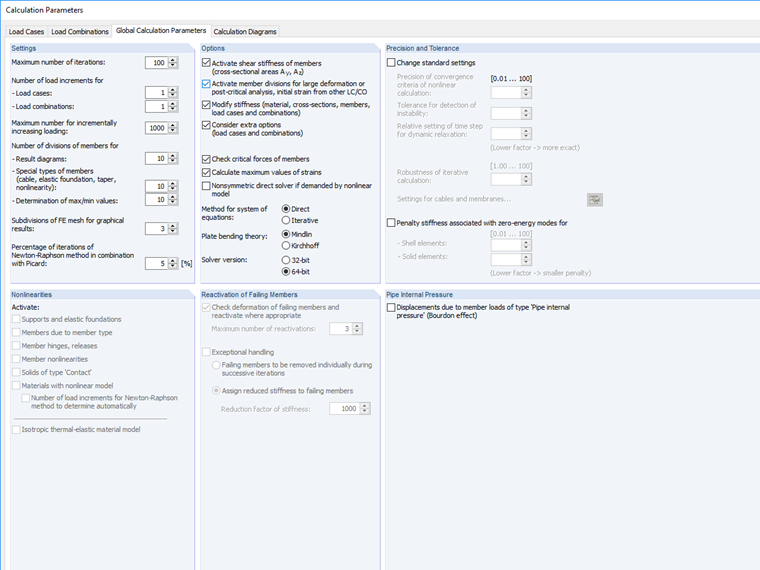
В программе предел прерывания настраивается прямо в параметрах расчета.

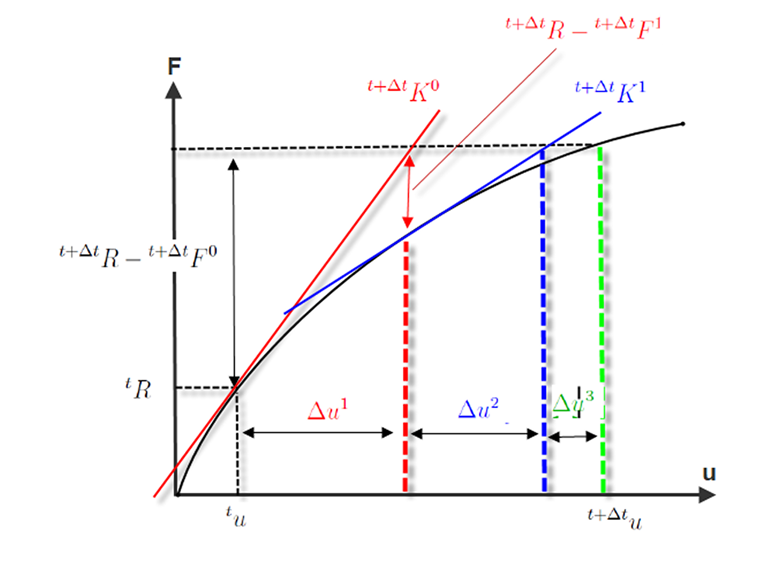
На следующем рисунке затем показан процесс итерации Ньютона-Рафсона. В первой итерации

предел прерывания R или ε не достигнут. Также во второй итерации (обозначено красным) предел допуска не достигается. Только в третьей итерации становится расстояние касательной жесткости настолько малым, что расчет достигает сходимости.

Как уже упоминалось раньше, в ходе итерации деформации постоянно суммируются.

Заключение

Итерация Ньютона-Рафсона обладает консистентностью, и соответственно, сходимостью второго порядка, причем количество «правильных» точек итерации с каждым шагом удваивается. В результате так итерация Ньютона-Рафсона сходится квадратично, и в случае достижения сходимости ее точность с каждой итерацией увеличивается. Однако, если данным методом нельзя достичь сходимости, то ошибка повторяется бесконечно и вычисление прерывается.

Ошибку расчета чаще всего вызывает либо слишком сильный наклон кривой зависимости деформаций от нагрузки, либо слишком малый наклон кривой в области пластических деформаций. С другой стороны, если кривая зависимости деформации от нагрузки на вышеприведенном рисунке показывает слишком сильный излом на втором шаге итерации, то касательная материала и, следовательно, матрица жесткости не будут правильно отображать наклон упругой области. Потому что в таком случае был бы подъем нулевой точки для пластической области неправильным. Это в принципе и есть одна из причин, по которой увеличение количества шагов нагрузки сопровождается улучшением сходимости.