Métodos de resolução de equações para cálculos não lineares

Introdução

O método dos elementos finitos é sempre utilizado quando os problemas mecânicos não podem ser resolvidos analiticamente. Frequentemente, os efeitos não lineares, tais como rotura sob pressão (não linearidade geométrica), plastificações (não linearidade do material) e graus de liberdade de contacto ou cinemáticos, também são considerados. Esses efeitos, especialmente no caso de modelos de material não lineares, podem ser considerados através de um método de cálculo iterativo.

Configuração MEF

Passos básicos para a configuração do MEF (mais informação pode ser encontrada em {%>

1. Forma fraca do equilíbrio
   $${\int }_B\underset{nichtlinearer Anteil}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   δu	Virtuelle (Test-)Verschiebung
   t0	Anfangslastfaktor
   σdV	Innere Kräfte
   ρbdV	Volumenkräfte
   B	integriertes Gebiet

   Forma fraca
2. Conversão para a notação de Voigt com o tensor 4 Passo
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Volumenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Oberflächenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	Steifigkeitsmatrix
   δε	Variation des Verzerrungszustands
   B	integriertes Gebiet
   ε	Dehnung
   u	Verformung

   Forma fraca na notação Voigt
3. Esta notação é utilizada no seguinte texto para resolver a solução aproximada da abordagem de EF para materiais não lineares.
4. Para isso, o campo de deslocamento é multiplicado pelas funções de abordagem.
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u(x,t)	Verschiebung über Zeit (Lastinkrement)
   H	Formfunktion
   û	Knotenverschiebung

   Campo de deslocamento através da função de teste

Inserir a derivada do deslocamento na forma fraca. A integração numérica é utilizada para calcular o deslocamento nodal, as tensões e as deformações no pós-processamento através da regra dos materiais.

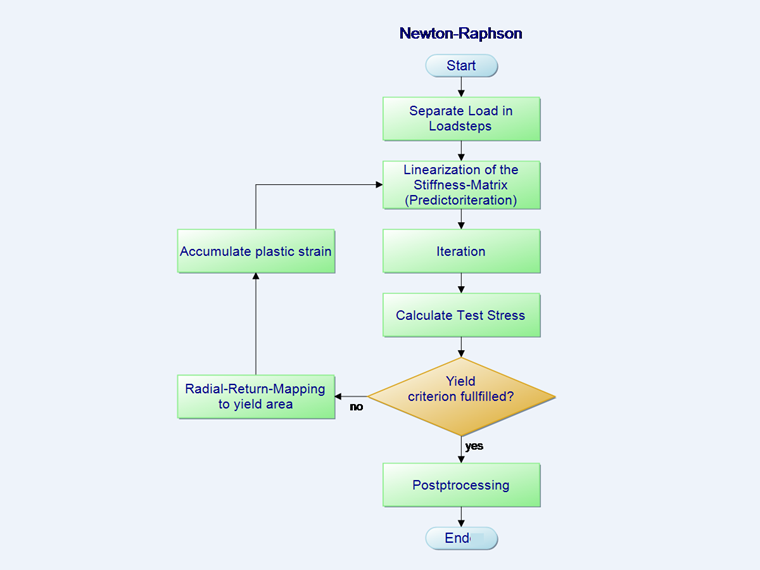
Sequência de iteração de Newton-Raphson

Devido ao comportamento do material não linear, a matriz de material C na Equação 2 acima muda com cada passo de expansão. O método de cálculo padrão para resolver este problema é a iteração Newton-Raphson. É utilizada para linearizar a função num ponto de início. A matriz de rigidez C do passo preliminar é sempre utilizada na iteração. No passo de iteração linearizada, é colocada uma tangente no zero da função.

As equações pertencentes ao fluxograma na imagem acima são as seguintes:

1. Subdividir a carga em intervalos de carga.
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fext	Äußere Last
   t	Zeit/Lastschritt
   Δf	Neues Lastinkrement

   Carga em intervalos de carga
2. Passo de predição
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	Steifigkeitsmatrix des vorherigen Zeitschritts
   t+Δtfext	Äußere Kräfte um eine weitere Laststufe erhöht
   0tfint	Innere Kräfte des vorherigen Zeitschritts
   ϕ	Verzerrung

   Previsão do passo
3. No ponto 3, iteração do diagrama de fluxo, é calculada a distorção total reduzida pela distorção plástica (passo de correcção). O objetivo do cálculo iterativo é sempre que a soma das cargas seja sempre zero. No entanto, isso é numericamente impossível. Portanto, é definido um limite de interrupção ε no qual o cálculo é interrompido como suficientemente preciso.
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   R	Abbruchrate
   fext	äußere Kräfte
   fint	innere Kräfte
   ε	Epsilon Abbruchrate
   t	Zeitschritt

   Limite de corte

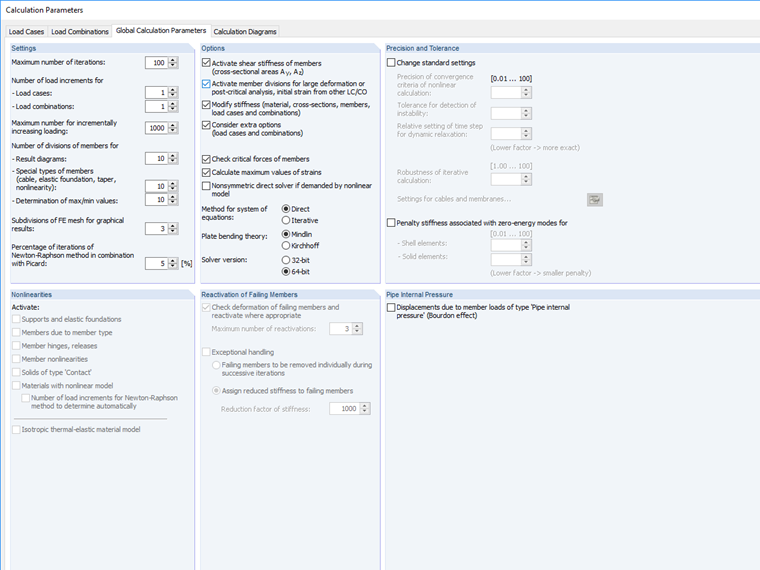
No programa, o limite de interrupção pode ser definido entre os parâmetros de cálculo.

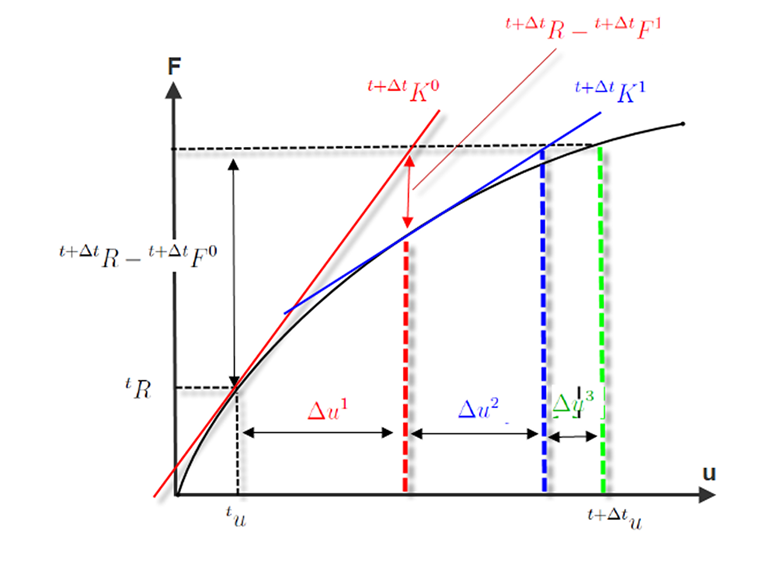
A imagem seguinte mostra o fluxo de uma iteração Newton-Raphson. Na primeira iteração

o ponto de paragem R ou ε não foi alcançado. O limite de tolerância também não é alcançado na segunda iteração (red). Apenas na terceira iteração é que a distância da rigidez da tangente é tão pequena que é alcançada a convergência.

Como já mencionado, a deformação é continuamente somada durante a iteração.

Conclusão

A iteração Newton-Raphson tem uma consistência ou ordem de convergência 2. O número de posições "corretas" na iteração duplica a cada passo. Assim, uma iteração Newton-Raphson converge quadraticamente, e a precisão aumenta com cada iteração quando o método converge. No entanto, se o método não converge, o erro vai para o infinito e o cálculo é interrompido.

As causas de erro são, por exemplo, uma inclinação demasiado inclinada da curva carga-deformação e uma inclinação da curva demasiado plana na zona plástica. Se a curva carga-deformação na figura acima apresenta uma ruptura demasiado forte no segundo passo de iteração, a tangente do material e, portanto, a matriz de rigidez não exibe corretamente a inclinação da zona elástica. Neste caso, a inclinação da raíz estaria errada para a área plástica. Esta é uma das razões pelas quais um aumento nos incrementos de carga é acompanhado por uma convergência melhor.