非线性方程求解方法

介绍

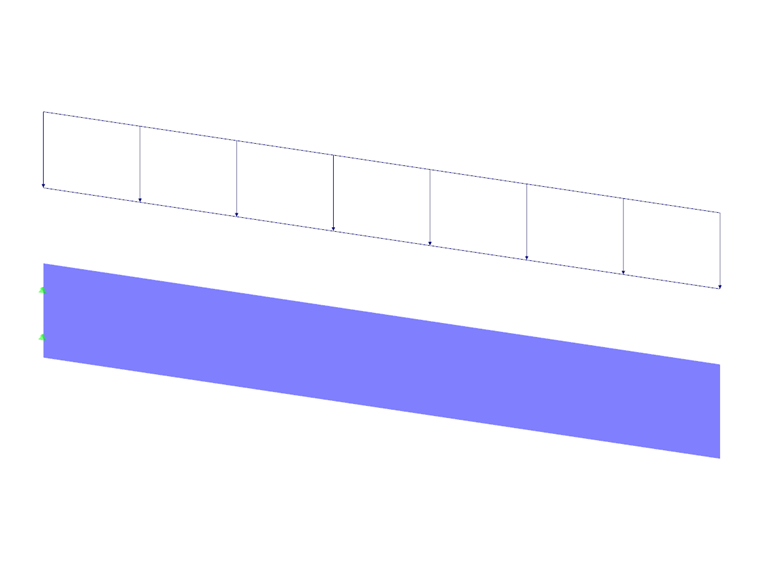
每当力学问题无法通过解析方法解决时，就可以使用有限元法。 通常，例如受压失效（几何非线性）、塑性屈服（材料非线性）以及接触或运动自由度等非线性影响也会被考虑。 可以通过使用迭代计算方法来考虑这些影响，特别是对于非线性材料模型。

• 3D Viewer | Google
• 3D Viewer | Babylon
• 虚拟现实

1 悬臂塑性行为

有限元模型设置

设置有限元模型的基本步骤（更多信息请参见[1]）：

1. 弱平衡形式
   $${\int }_B\underset{nichtlinearer Anteil}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   δu	虚拟（测试）位移
   t0	初始荷载系数
   σdV	内力
   ρbdV	实体力
   B	综合面积

   弱形式
2. 将张量 4 转换为 Foigt 表示法 踏步
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Volumenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Oberflächenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	刚度矩阵
   δε	应变状态的变化
   B	综合面积
   ε	Strain
   U	变形

   Voigt表示法中的弱形式
3. 在下文中使用这个符号来求解非线性材料的有限元方法的近似解。
4. 为此，位移场乘以逼近函数。
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u（x，t）	随时间推移的位移（荷载增量）
   H	表格功能
   û	节点位移

   试件的位移场

将位移导数插入弱形式中。 数值积分可用于计算节点位移、应力，以及在后期处理中按照材料组合的规定进行计算。

Newton-Raphson 迭代顺序

由于材料是非线性的，公式 2 中的材料矩阵 C 会随着每个扩展步的变化而变化。 求解此问题的标准计算方法是 Newton-Raphson 迭代。 用于使函数在起点处线性化。 迭代中始终使用初始步的刚度矩阵 C。 在线性迭代步骤中，在函数的零点处放置切线。

2 Newton-Raphson迭代

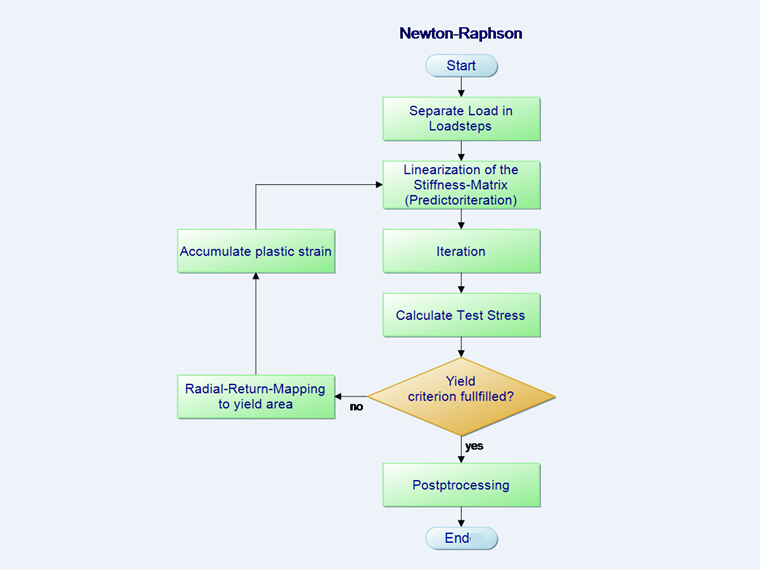
上图中的流程图中的公式如下：

1. 将荷载划分为多个荷载步。
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fext	外部荷载
   t	时间/荷载步长
   Δf	新的荷载增量

   荷载步阶荷载
2. 预测步长
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	上一个时间步的刚度矩阵
   t + Δt fext	外力随荷载的增加而增加
   0t[F12]int	上一个时间步的内力
   ϕ	Strain

   预测步骤
3. 在第 3 点，流程图的迭代中，计算总变形减去塑性变形后的结果（修正步骤）。 迭代计算的目标是使荷载之和始终为零。 但这在数值上是不可能的。 因此，定义了一个中断极限 ε，在该极限数目时计算由于足够精度而中断。
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   R	破坏极限
   fext	外力
   [F12]int	内力
   ε	厄普西隆极限进入极限
   t	时间步

   到达极限

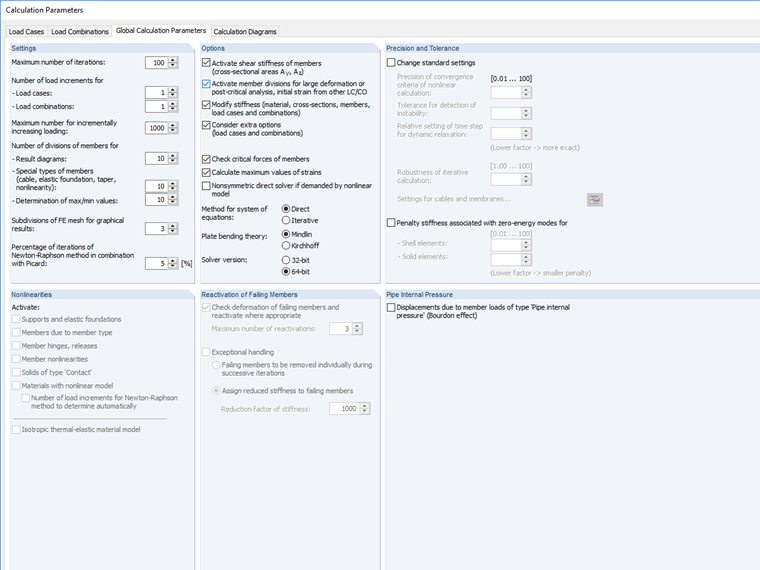
在程序中，可以设置折断极限值的计算参数。

3 计算参数

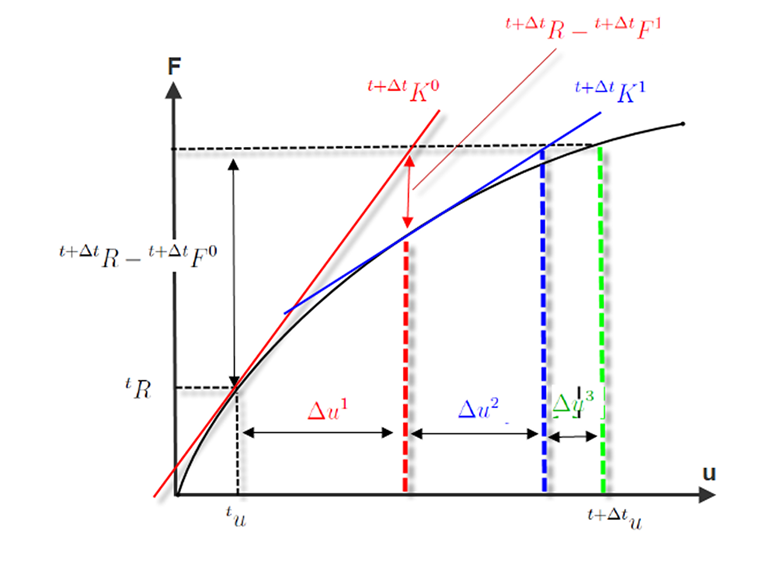
下图显示了Newton-Raphson迭代的流程。 在第一次迭代中

4 Newton-Raphson迭代图

如前所述，在迭代过程中变形会被连续叠加。

概述总结

Newton-Raphson 迭代的一致性或收敛阶数为 2。 迭代中“正确”位置的数量每增加一倍。 Newton-Raphson 迭代以二次函数的方式收敛，随着迭代的进行，当方法收敛时，精度提高。 如果该方法不收敛，则误差无穷大，计算停止。

例如，荷载-变形曲线的斜率太陡以及塑性区域中的曲线斜率太平， 如果上图中的荷载-变形曲线在第二次迭代步中出现突变，那么材料切线以及刚度矩阵将无法正确显示弹性区域的斜率。 在这种情况下，根部的倾角对于塑性区域是错误的。 这就是为什么随着荷载步的增加收敛会越来越快的原因。

知识库

知识库 001662 | 非线性计算的方程求解方法