Metody řešení rovnic při nelineárních výpočtech

Úvod

Pokud nelze mechanické úlohy řešit analyticky, uplatňuje se metoda konečných prvků. Přitom se často berou v úvahu také nelineární účinky jako neúčinnost v tlaku (geometrická nelinearita), plastifikace (materiálová nelinearita) a kontaktní, respektive kinematické stupně volnosti. Tyto účinky, zejména v případě nelineárních materiálových modelů, lze zohlednit iterační metodou výpočtu.

Formulace MKP

Základní kroky pro nastavení MKP (další informace najdete v [1]):

1. Slabá formulace rovnováhy
   $${\int }_B\underset{\mathrm{nelineární} \mathrm{složka}}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   δu	Virtuelle (Test-)Verschiebung
   t0	Anfangslastfaktor
   σdV	Innere Kräfte
   ρbdV	Volumenkräfte
   B	integriertes Gebiet

   Slabá formulace
2. Převod na Voigtův zápis tenzoru čtvrtého Krok
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Objemové} \mathrm{síly}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Povrchové} \mathrm{síly}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	Steifigkeitsmatrix
   δε	Variation des Verzerrungszustands
   B	integriertes Gebiet
   ε	Dehnung
   u	Verformung

   Slabá formulace ve Voigtově zápisu
3. Z tohoto zápisu dále vychází aproximační řešení MKP u nelineárních materiálů.
4. Pole posuvů se přitom násobí tvarovými funkcemi.
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u(x,t)	Verschiebung über Zeit (Lastinkrement)
   H	Formfunktion
   û	Knotenverschiebung

   Pole posuvů upravené tvarovou funkcí

Použití derivace posunutí ve slabé formulaci. Numerickou integrací se stanoví posunutí uzlů a v post processingu napětí a přetvoření na základě materiálového modelu.

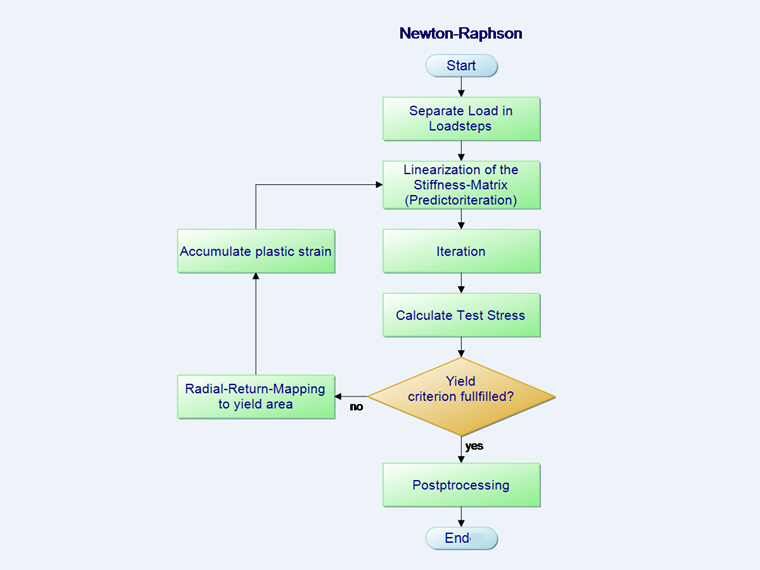
Průběh Newton-Raphsonovy iterace

Vlivem nelineárního chování materiálu se materiálová matice C ve výše uvedené rovnici 2 mění s každým krokem přetvoření. Standardní metodou řešení tohoto problému je takzvaná Newton-Raphsonova iterace. Při ní se funkce ve výchozím bodě linearizuje. Při iteraci se vždy používá matice tuhosti C předchozího kroku. V linearizovaném iteračním kroku je tečna vedena k nulovému bodu funkce.

Ke schématu průběhu iterace na obrázku výše patří následující rovnice:

1. Rozložení zatížení do zatěžovacích kroků
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fext	Äußere Last
   t	Zeit/Lastschritt
   Δf	Neues Lastinkrement

   Zatížení v zatěžovacích krocích
2. Krok predikce
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	Steifigkeitsmatrix des vorherigen Zeitschritts
   t+Δtfext	Äußere Kräfte um eine weitere Laststufe erhöht
   0tfint	Innere Kräfte des vorherigen Zeitschritts
   ϕ	Verzerrung

   Krok predikce
3. V bodě 3 Iterace vývojového diagramu se vypočítá celkové přetvoření po odečtení plastického přetvoření (krok korekce). Cílem iteračního výpočtu vždy je, aby součet zatížení byl nulový. To ovšem numericky není možné. Proto se definuje mez pro přerušení ε, při které se výpočet přeruší jako dostatečně přesný.
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   R	Abbruchrate
   fext	äußere Kräfte
   fint	innere Kräfte
   ε	Epsilon Abbruchrate
   t	Zeitschritt

   Mez pro přerušení

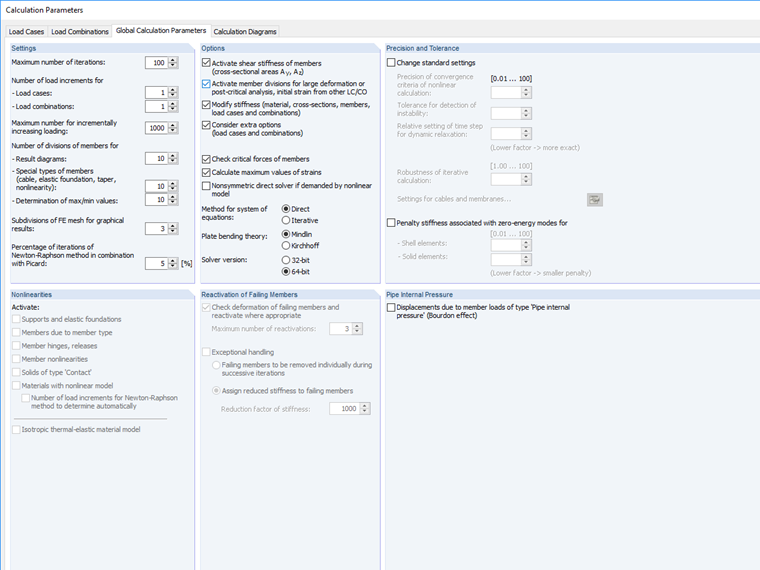
V programu lze mez pro přerušení nastavit v parametrech výpočtu.

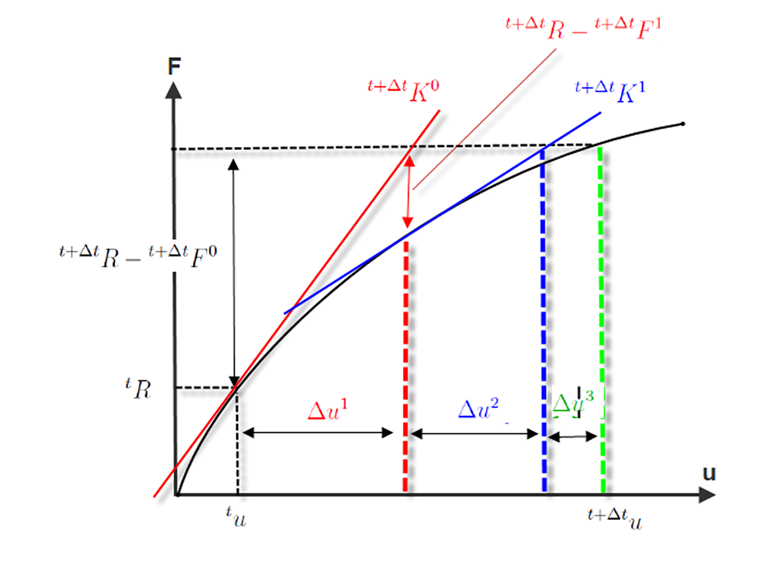
Na následujícím obrázku je znázorněn průběh Newton-Raphsonovy iterace. V první iteraci

není dosažena mez pro přerušení R, respektive ε. Ani v druhé iteraci (červeně) není dosažena mez tolerance. Až ve třetí iteraci je vzdálenost tečné tuhosti tak malá, že je dosažena konvergence.

Jak jsme již zmínili, deformace se během iterace průběžně sčítají.

Závěr a výhled

Newton-Raphsonova iterace je metoda druhého řádu konzistence, respektive konvergence. Počet „správných“ míst iterace se s každým krokem zdvojnásobuje. Newton-Raphsonova iterační metoda tak konverguje kvadraticky a přesnost je s každou iterací vyšší, pokud dochází ke konvergenci. Pokud však metoda nekonverguje, chyba jde do nekonečna a výpočet se přeruší.

Příčinou chyby bývá například příliš strmý sklon křivky závislosti deformace na zatížení a příliš mírný sklon křivky v plastické oblasti. Pokud by křivka závislosti deformace na zatížení na výše uvedeném obrázku vykazovala v druhém iteračním kroku příliš velký vzpěr, tečna materiálu, a tudíž matice tuhosti by neznázorňovala správně stoupání pružné oblasti. Stoupání u nulového místa by bylo v tomto případě pro plastickou oblast nesprávné. To je jeden z důvodů, proč vyšší počet zatěžovacích kroků doprovází lepší konvergence.