Méthodes de résolution d’équations pour les calculs non linéaires

Présentation

La méthode des éléments finis est utilisée lorsque des problèmes mécaniques ne peuvent pas être résolus analytiquement. Les effets non linéaires tels que l’échec sous compression (non-linéarité géométrique), les plastifications (non-linéarité de matériau) et les degrés de liberté de contact ou cinématiques sont également pris en compte. Ces effets, en particulier pour les modèles de matériaux non linéaires, peuvent être considérés à l’aide d’une méthode de calcul itérative.

Approche par la méthode aux éléments finis

Voici les étapes essentielles pour une approche par la méthode aux éléments finis (plus d'informations sont disponibles dans {%}#Refer [1]]]) :

1. Forme faible de l’équilibre
   $${\int }_B\underset{nichtlinearer Anteil}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   Δu	Déplacement virtuel (d'essai)
   t0	Facteur de charge initial
   σdV	efforts internes
   ρbdV	Forces des solides
   B	Zone intégrée

   Forme faible
2. Transformation selon la notation de Voigt avec un tenseur d’ordre 4. Étape
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Volumenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Oberflächenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	Matrice de rigidité
   δε	Variation de l'état de déformation
   B	Zone intégrée
   ε	déformation
   U	Déformation

   Forme faible dans la notation Voigt
3. Cette notation est utilisée dans ce qui suit pour résoudre la solution approximative de l'approche aux EF pour les matériaux non linéaires.
4. Pour ce faire, le champ de déplacement est multiplié par les fonctions d’approche.
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u (x, t)	Déplacement dans le temps (incrément de charge)
   h	Fonction de formulaire
   û	Déplacement nodal

   Champ de déplacement via la fonction d'essai

La dérivée du déplacement est insérée dans la forme faible. L’intégration numérique est utilisée pour calculer le déplacement nodal, les contraintes et déformations lors du post-traitement à l’aide de la règle de matériau.

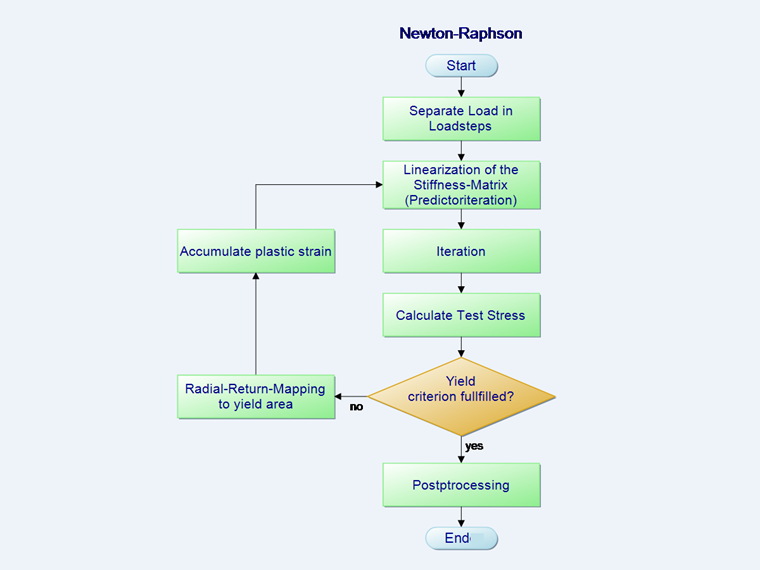
Séquence des itérations de Newton-Raphson

En raison du comportement non linéaire du matériau, la matrice de matériau C dans l’équation 2 ci-dessus change à chaque étape d’expansion. La méthode de calcul standard pour résoudre ce problème est l’itération de Newton-Raphson. Elle est utilisée pour linéariser une fonction à un point de départ. Dans l’itération, la matrice de rigidité C de l’étape précédente est toujours utilisée. Dans l'étape d’itération linéarisée, une tangente est placée au zéro de la fonction.

Les équations correspondant à la méthode représentée par un schéma sur la figure ci-dessus sont les suivantes :

1. Division de la charge en pas de charge.
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fext	Charge externe
   t	Temps/pas de charge
   Δf	Nouvel incrément de charge

   Charge par pas de charge
2. Étape d’indication
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	Matrice de rigidité du pas de temps précédent
   t + Δ t fext	Efforts externes augmentés d'un pas de charge supplémentaire
   0tfint	Efforts internes du pas de temps précédent
   ϕ	déformation

   Étape de prédiction
3. Durant la troisième étape de cette méthode, la distorsion totale réduite par la déformation plastique est calculée (étape de correction). L’objectif du calcul itératif est toujours que la somme des charges soit nulle. Ce n’est cependant pas possible numériquement. Une limite de rupture ε à partir de laquelle le calcul s’arrête car suffisamment précis est donc définie.
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   r	Limite de rupture
   fext	Forces externes
   fint	efforts internes
   ε	Limite de rupture d'Epsilon
   t	Pas de temps

   Limite de rupture

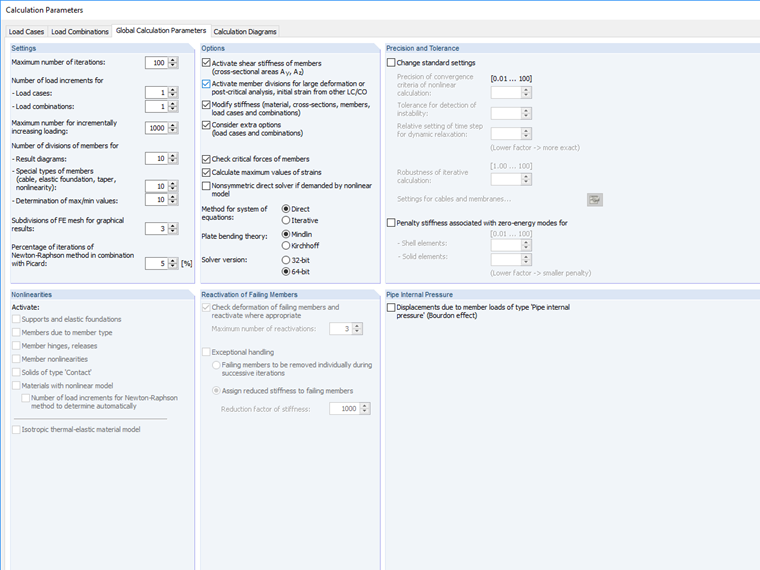
Cette limite peut être définie dans les paramètres de calcul du logiciel.

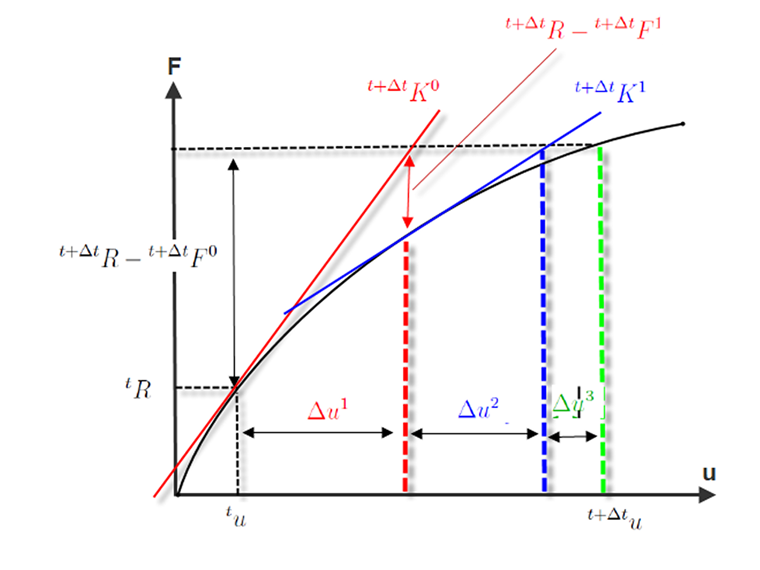
La figure suivante montre le déroulement d’une itération Newton-Raphson. Dans la première itération,

la rupture R ou ε n’est pas atteinte. La limite de tolérance n’est pas non plus atteinte dans la deuxième itération (en rouge). La distance de la rigidité tangente est assez faible pour atteindre la convergence dans la troisième itération seulement.

Comme déjà mentionné, la déformation est continuellement additionnée pendant l’itération.

Conclusion

L’itération Newton-Raphson est cohérente ou converge avec l’ordre 2. Le nombre de chiffres corrects est doublé à chaque étape. Ainsi, une itération Newton-Raphson converge de manière quadratique et sa précision augmente à chaque itération lorsque la méthode converge. Cependant, si la méthode ne converge pas, elle entre en boucle infinie et le calcul s’arrête.

Les causes d’erreur sont par exemple une pente trop raide de la courbe charge-déformation et une courbure trop faible dans le domaine d’élasticité. Si la courbe de la figure ci-dessus présentait une rupture trop importante dans la deuxième étape d’itération, la tangente du matériau et donc la matrice de rigidité ne représenteraient pas correctement la variation du domaine d’élasticité. Dans ce cas, la courbe représentant la racine serait incorrecte pour le domaine de plasticité. C’est l’une des raisons pour lesquelles une augmentation des pas de charge permet d’améliorer la convergence.