Métodos de resolución de ecuaciones para cálculos no lineales

Introducción

El método de los elementos finitos se usa cuando los problemas mecánicos no se pueden resolver analíticamente. A menudo, también se tienen en cuenta efectos no lineales como el fallo por compresión (no linealidad geométrica), las plastificaciones (no linealidad del material) y los grados de libertad de contacto o cinemáticos. Estos efectos, especialmente en el caso de modelos de materiales no lineales, se pueden considerar utilizando un método de cálculo iterativo.

Configuración del método de los elementos finitos (MEF)

Pasos básicos para la configuración del MEF (puede encontrar más información en [1]):

1. Forma débil del equilibrio
   $${\int }_B\underset{nichtlinearer Anteil}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   δu	Desplazamiento virtual (prueba)
   t0	Factor de carga inicial
   σdV	Esfuerzos internos
   ρbdV	Fuerzas sólidas
   B	Área integrada

   Forma débil
2. Conversión a la notación Voigt con tensor 4 Paso
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Volumenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Oberflächenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	matriz de rigidez
   δε	Variación del estado de deformación
   B	Área integrada
   ε	deformación
   U	Deformación

   Forma débil en la notación de Voigt
3. Esta notación se usa a continuación para resolver la solución aproximada del planteamiento por elementos finitos para materiales no lineales.
4. Para esto, el campo de desplazamiento se multiplica por las funciones de aproximación.
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u (x, t)	Desplazamiento en el tiempo (incremento de carga)
   h	Función de forma
   û	desplazamiento en nudo

   Campo de desplazamiento mediante la función de prueba

Inserción de la derivada del desplazamiento en la forma débil. La integración numérica se usa para calcular el desplazamiento en nudos y las tensiones y deformaciones en el posprocesamiento por medio de la regla del material.

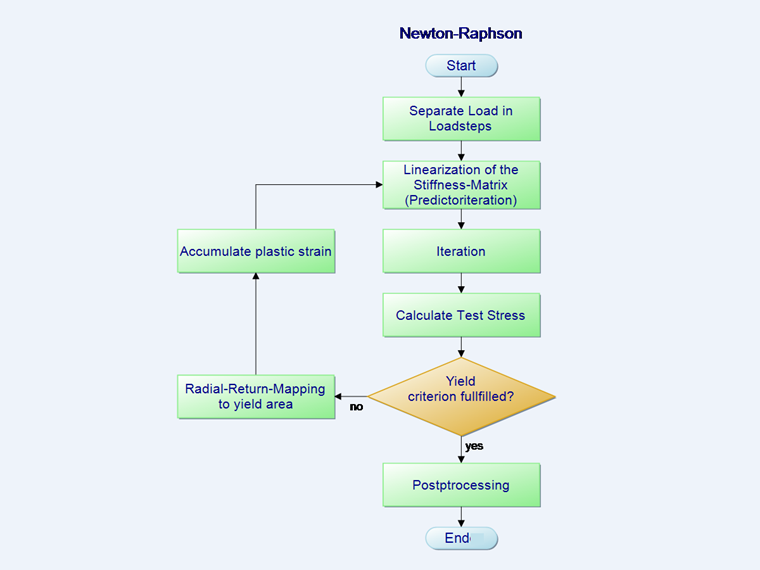
Secuencia de iteración de Newton-Raphson

Debido al comportamiento no lineal del material, la matriz del material C en la ecuación 2 anterior cambia con cada paso de expansión. El método de cálculo estándar para resolver este problema es la llamada iteración de Newton-Raphson. Se usa para hacer lineal la función en un punto de partida. En la iteración, siempre se usa la matriz de rigidez C del paso preliminar. En el paso de la iteración linealizada, se coloca una tangente en el cero de la función.

Las ecuaciones que pertenecen al diagrama de flujo en la figura anterior son las siguientes:

1. División de la carga en pasos de carga.
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fext	Carga externa
   t	Tiempo/paso de carga
   Δf	Nuevo incremento de carga

   Carga en pasos de carga
2. Paso de indicador
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	Matriz de rigidez del paso de tiempo anterior
   t+Δtfext	Fuerzas externas incrementadas por un paso de carga adicional
   0tfint	Fuerzas internas del paso de tiempo anterior
   ϕ	Deformación

   Paso de predicción
3. En el punto 3, iteración del diagrama de flujo, se calcula la distorsión total reducida por la distorsión plástica (paso de corrector). El objetivo del cálculo iterativo es siempre que la suma de las cargas sea cero. Sin embargo, esto no es posible numéricamente. Por lo tanto, se define un límite de interrupción ε en el que se interrumpe el cálculo cuando sea lo suficientemente preciso.
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   R	Límite de interrupción
   fext	Fuerzas externas
   fint	Esfuerzos internos
   ε	Límite de interrupción de épsilon
   t	Paso de tiempo

   Límite de interrupción

En el programa, el límite de interrupción se puede establecer entre los parámetros de cálculo.

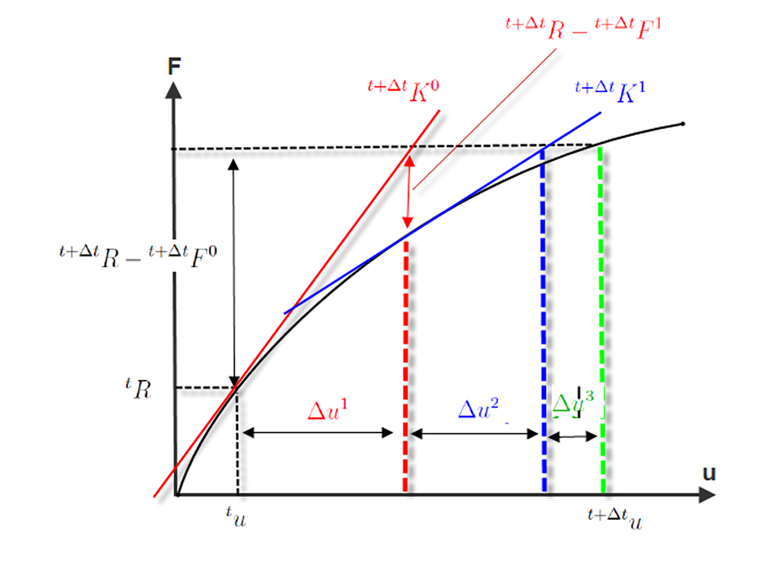
La figura siguiente muestra el flujo de una iteración de Newton-Raphson. En la primera iteración

no se alcanza la interrupción R o ε. El límite de tolerancia tampoco se alcanza en la segunda iteración (en rojo). Solo en la tercera iteración, la distancia de la rigidez de la tangente es tan pequeña que se logra la convergencia.

Como ya se mencionó, la deformación se suma continuamente durante la iteración.

Conclusión

La iteración de Newton-Raphson tiene la consistencia o el orden de convergencia 2. El número de posiciones "correctas" en la iteración se duplica con cada paso. Por lo tanto, una iteración de Newton-Raphson converge cuadráticamente y la precisión aumenta con cada iteración cuando el método converge. Sin embargo, si el método no converge, el error llega al infinito y se detiene el cálculo.

Las causas del error son, por ejemplo, una pendiente demasiado fuerte de la curva carga-deformación y una pendiente demasiado plana de la curva en el área plástica. Si la curva carga-deformación en la figura anterior mostrara una interrupción demasiado fuerte en el segundo paso de iteración, la tangente del material y, por lo tanto, la matriz de rigidez no mostrarían correctamente la pendiente del área elástica. En este caso, la pendiente de la raíz sería incorrecta para el área plástica. Esta es una de las razones por las que un aumento en los pasos de carga va acompañado de una convergencia mejorada.