Metody rozwiązywania równań w obliczeniach nieliniowych

Wstęp

Metoda elementów skończonych jest każdorazowo stosowana w przypadkach, gdy problemów mechanicznych nie sposób rozwiązać analitycznie. Często w modelu uwzględniane są również efekty nieliniowe, takie jak uszkodzenie pod wpływem docisku (nieliniowość geometryczna), uplastycznienie (nieliniowość materiału) oraz zagadnienie kontaktu lub kinematyczne stopnie swobody. Wpływy te, zwłaszcza w przypadku nieliniowych modeli materiałowych, można uwzględnić przy użyciu iteracyjnej metody obliczeń.

Formulacja MES

Podstawowe kroki dla ustawiania MES (dalsze informacje można znaleźć w [1]):

1. Słaba postać równań równowagi
   $${\int }_B\underset{nichtlinearer Anteil}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   ΔU	Wirtualne przemieszczenie (testowe)
   t0	Początkowy współczynnik obciążenia
   σdV	siły wewnętrzne
   ρbdV	Siły bryłowe
   B	Obszar zintegrowany

   Słaba forma
2. Konwersja na notację Voigta z wykorzystaniem tensora 4 Stopień
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Volumenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Oberflächenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	macierz sztywności
   δε	Zmiana stanu odkształcenia
   B	Obszar zintegrowany
   ε	odkształcenie
   U	odkształcenie

   Słaba forma w notacji Voigta
3. Notacja ta jest używana w dalszej części opracowania do przybliżonego rozwiązania równań MES dla materiałów nieliniowych.
4. W tym celu pole przemieszczeń pomnożone zostaje przez funkcje podejścia.
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u (x, t)	Przemieszczenie w czasie (przyrost obciążenia)
   h	Funkcja formularza
   û	przemieszczenie węzłowe

   Pole przemieszczenia za pomocą funkcji trial

Podstawienie pochodnej przemieszczenia do postaci słabej. Zastosowane jest całkowanie numeryczne do obliczania przemieszczeń węzłowych, a następnie naprężeń i odkształceń w późniejszej fazie obróbki danych za pomocą przyjętego modelu materiałowego.

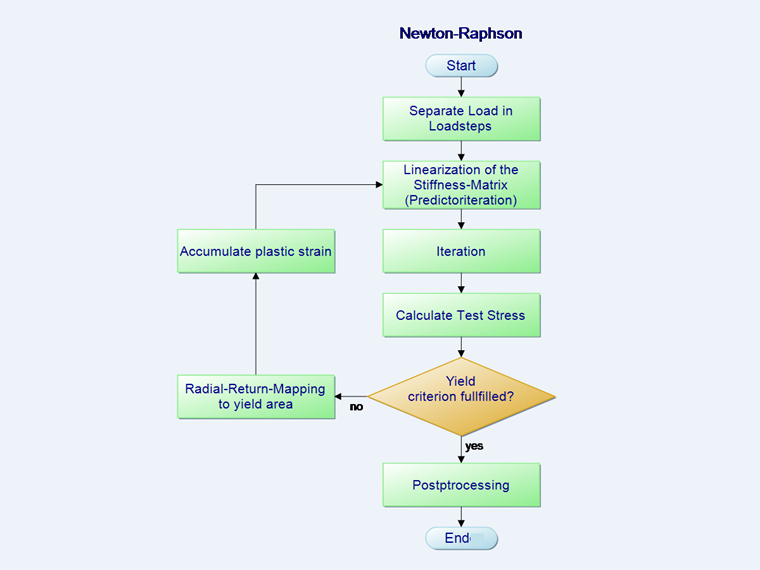
Sekwencja iteracji Newtona-Raphsona

Ze względu na nieliniowe zachowanie materiału, macierz materiału C w równaniu 2 zmienia się z każdym krokiem. Standardową metodą obliczeniową dla rozwiązania tego problemu jest tak zwana iteracja Newtona-Raphsona. Służy do linearyzacji funkcji w punkcie początkowym. W iteracji zawsze stosowana jest macierz sztywności C kroku wstępnego. W zlinearyzowanym kroku iteracji styczna jest umieszczana w punkcie zerowym funkcji.

Równania ujęte w schemacie blokowym na powyższym rysunku są następujące:

1. Podział obciążenia na kroki obciążenia.
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fzewn	Obciążenie zewnętrzne
   t	Krok czas/obciążenie
   Δf	Nowy przyrost obciążenia

   Obciążenie w krokach obciążenia
2. Krok prognostyczny
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	Macierz sztywności z poprzedniego kroku czasowego
   t + Δ t fzewn	Siły zewnętrzne zwiększone o kolejny krok obciążenia
   [LinkToImage09]tFint	Siły wewnętrzne poprzedniego kroku czasowego
   ϕ	odkształcenie

   Krok predyktora
3. W punkcie 3 schematu (iteracja), obliczane jest całkowite odkształcenie pomniejszone o odkształcenie plastyczne (etap korekty). Celem obliczeń iteracyjnych jest zawsze to, aby suma obciążeń zewnętrznych i sił wewnętrznych wynosiła zero. Z numerycznego punktu widzenia nie jest to jednak możliwe. Dlatego definiuje się granicę przerwania iteracji ε, przy której obliczenia nie są kontynuowane jako wystarczająco dokładne.
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   [SCHOOL.SCHOOLORINSTITUTION]	Granica zerwania
   fzewn	Siły zewnętrzne
   Fint	siły wewnętrzne
   ε	Granica oderwania epsilonu
   t	Krok czasowy

   Granica zerwania

W programie można ustawić granicę ε przerwania obliczeń w parametrach obliczeniowych.

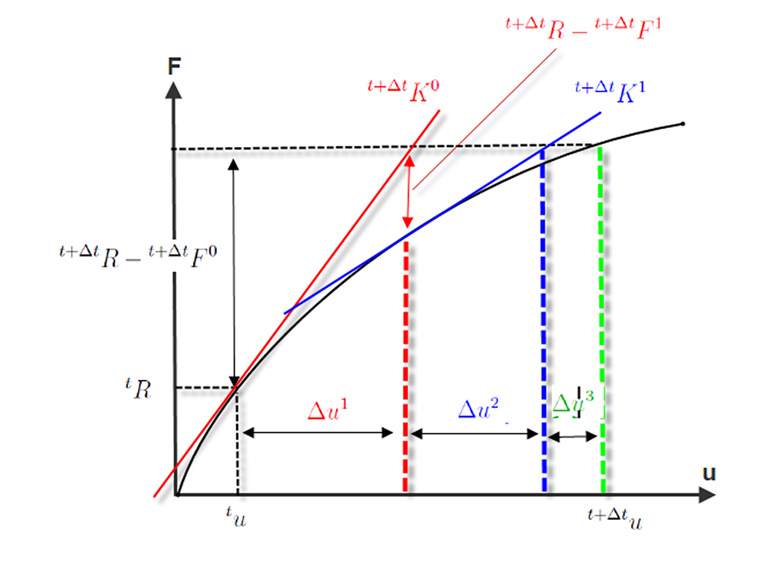
Poniższy rysunek pokazuje przebieg iteracji Newtona-Raphsona. W pierwszej iteracji

granica przerwania obliczeń R lub ε nie zostaje osiągnięta. Granica tolerancji również nie została osiągnięta w drugiej iteracji (kolor czerwony). Dopiero w trzeciej iteracji odległość aproksymowanej sztywności stycznej od tej rzeczywistej jest na tyle mała, że osiąga się zbieżność.

Jak już wspomniano, odkształcenie jest podczas iteracji sumowane w sposób ciągły.

Uwagi końcowe

Metoda iteracyjna Newtona-Raphsona ma spójność lub rząd zbieżności 2. Liczba „prawidłowych” lokalizacji w iteracji podwaja się z każdym krokiem. I tak, iteracja Newtona-Raphsona jest zbieżna kwadratowo, a dokładność wzrasta z każdą iteracją, gdy metoda jest zbieżna. Jeżeli jednak metoda nie jest zbieżna, błąd dąży do nieskończoności, a obliczenia zostają zatrzymane.

Przyczyny braku zbieżności to na przykład zbyt strome nachylenie krzywej obciążenie-odkształcenie lub zbyt małe nachylenie tej krzywej w obszarze plastycznym. Jeżeli krzywa obciążenie- deformacja na powyższym rysunku wykazywałaby zbyt dużą zmianę w drugim kroku iteracji, styczna materiału, a tym samym macierz sztywności, nie odwzorowywałaby prawidłowo nachylenia krzywej w obszarze sprężystym. W takim przypadku nachylenie krzywej dla rozwiązania cząstkowego byłoby nieprawidłowe w obszarze plastycznym. Jest to jeden z powodów, dla których wzrostowi w kroku obciążenia towarzyszy lepsza zbieżność.