Einführung
Die Finite-Elemente-Methode kommt immer dann zum Einsatz, wenn sich mechanische Problemstellungen analytisch nicht lösen lassen. Häufig werden hierbei auch nichtlineare Effekte wie Ausfall bei Druck (geometrische Nichtlinearität), Plastifizierungen (materielle Nichtlinearität) und Kontakt- beziehungsweise kinematische Freiheitsgrade berücksichtigt. Diese Effekte, insbesondere bei nichtlinearen Materialmodellen, lassen sich über eine iterative Berechnungsmethode berücksichtigen.
FEM-Formulierung
Grundlegende Schritte einer FEM-Formulierung (weitere Informationen finden sich in [1]):
- Schwache Form des Gleichgewichts
δu Virtuelle (Test-)Verschiebung t0 Anfangslastfaktor σdV Innere Kräfte ρbdV Volumenkräfte B integriertes Gebiet - Umformung in Voigt Notation mit Tensor 4. Stufe
C Steifigkeitsmatrix δε Variation des Verzerrungszustands B integriertes Gebiet ε Dehnung u Verformung
Mit dieser Notation wird im Weiteren die Näherungslösung des FE-Ansatzes bei nichtlinearen Materialien gelöst. - Das Verschiebungsfeld wird dazu mit den Ansatzfunktionen multipliziert.
u(x,t) Verschiebung über Zeit (Lastinkrement) H Formfunktion û Knotenverschiebung - Ableitung der Verschiebung in die schwache Form einsetzen. Über numerische Integration werden Knotenverschiebung und im Post Processing die Spannungen und Verzerrungen über das Stoffgesetz berechnet.
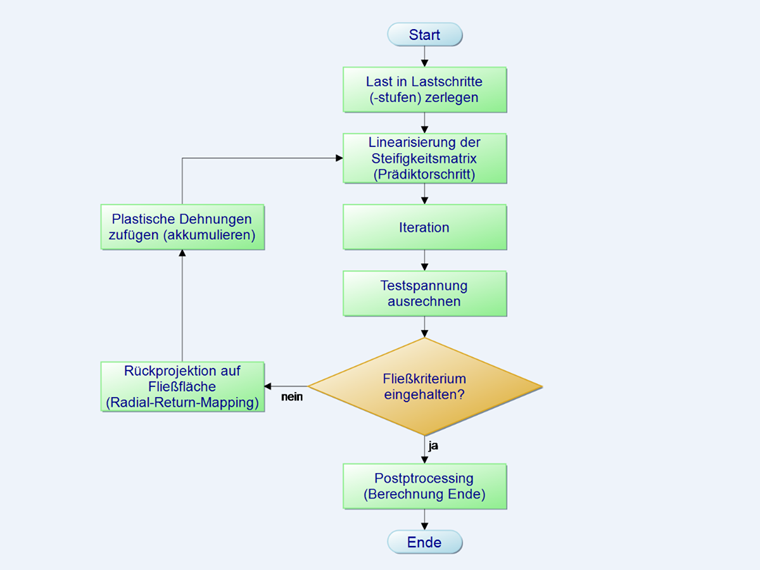
Ablauf einer Newton-Raphson-Iteration
Aufgrund des nichtlinearen Materialverhaltens ändert sich die Materialmatrix C in obiger Gleichung 2 mit jedem Dehnschritt. Das Standard-Rechenverfahren zur Lösung dieses Problems ist die sogenannte Newton-Raphson-Iteration. Mit ihr wird die Funktion in einem Ausgangspunkt linearisiert. In der Iteration wird immer die Steifigkeitsmatrix C des Vorschritts verwendet. In dem linearisierten Iterationsschritt wird eine Tangente an die Nullstelle der Funktion gelegt.
Die zum Ablaufschema im obigen Bild gehörenden Gleichungen:
- Last in Lastschritte zerlegen.
- Prädiktorschritt
K Steifigkeitsmatrix des vorherigen Zeitschritts t+Δtfext Äußere Kräfte um eine weitere Laststufe erhöht 0tfint
Innere Kräfte des vorherigen Zeitschritts ϕ Verzerrung - Im Punkt 3 Iteration des Ablaufschemas wird die Gesamtverzerrung abzüglich der plastischen Verzerrung berechnet (Korrektorschritt).
Das Ziel der iterativen Berechnung ist immer, dass die Summe der Lasten Null ergibt. Numerisch ist dies jedoch nicht möglich. Daher wird eine Abbruchrate ε definiert, bei der die Berechnung als ausreichend genau abgebrochen wird.
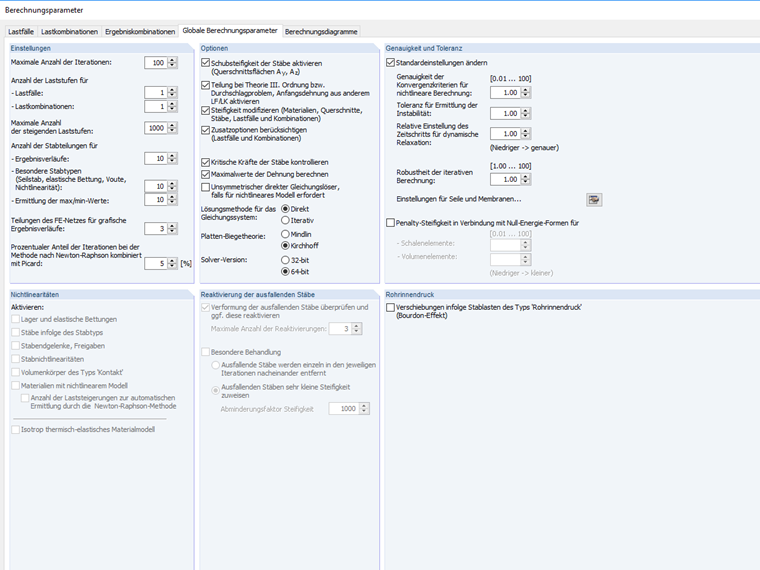
Im Programm kann die Abbruchrate unter den Berechnungsparametern gesteuert werden.
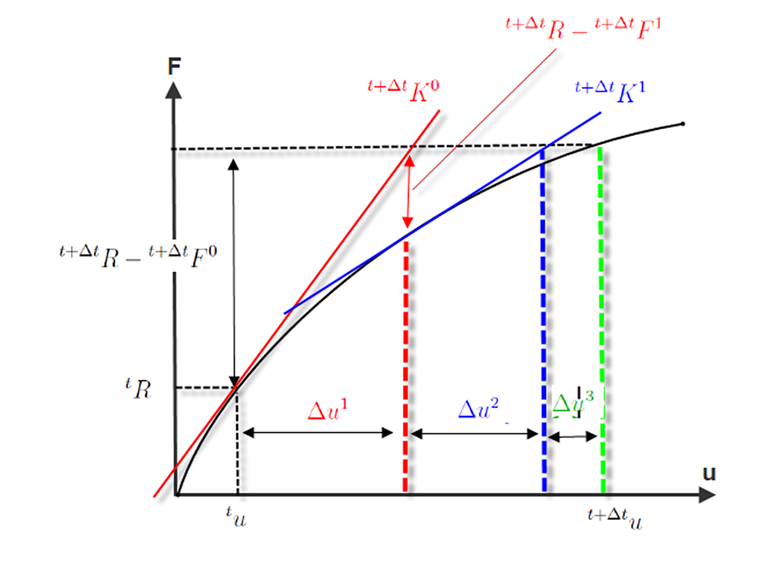
Im folgenden Bild wird der Ablauf einer Newton-Raphson-Iteration dargestellt. In der ersten Iteration
wird die Abbruchrate R beziehungsweise ε nicht erreicht. Auch in der zweiten Iteration (rot) wird die Toleranzschranke nicht erreicht. Erst in der dritten Iteration ist der Abstand der Tangentensteifigkeit so klein, dass Konvergenz erreicht wird.
Wie bereits erwähnt, wird die Verformung während der Iteration immer weiter aufsummiert.
Zusammenfassung
Die Newton-Raphson-Iteration hat die Konsistenz- beziehungsweise Konvergenzordnung 2. Die Anzahl der "richtigen" Stellen der Iteration verdoppelt sich bei jedem Schritt. Demzufolge konvergiert eine Newton-Raphson-Iteration quadratisch und die Genauigkeit wird mit jeder Iteration größer, wenn das Verfahren konvergiert. Wenn das Verfahren jedoch nicht konvergiert, geht der Fehler ins Unendliche und die Berechnung wird abgebrochen.
Fehlerursachen sind zum Beispiel eine zu starke Steigung der Last Verformungs-Kurve und zu flache Neigung der Kurve im plastischen Bereich. Wenn die Last-Verformungs-Kurve im obigen Bild im zweiten Iterationsschritt einen zu starken Knick aufwiese, würde die Materialtangente und damit die Steifigkeitsmatrix die Steigung des elastischen Bereichs nicht korrekt abbilden. Die Steigung der Nullstelle wäre in diesem Fall für den plastischen Bereich falsch. Dies ist einer der Gründe, weshalb eine Erhöhung der Lastschritte mit einer verbesserten Konvergenz einhergeht.
Dlubal_KohlA_]_LI.jpg?mw=350&hash=ee8d38f1c4853d80307fa156c159b5e78a3fdca9)
.jpg?mw=350&hash=8f312d6c75a747d88bf9d0f5b1038595900b96c1)
.jpg?mw=350&hash=196d91410dd36f58fcc8b0194f4577bb70cf53c3)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
