Metodi di risoluzione di equazioni per calcoli non lineari

Introduzione

Il metodo degli elementi finiti viene utilizzato nei casi in cui i problemi meccanici non possono essere risolti analiticamente. Spesso vengono presi in considerazione anche gli effetti non lineari come rottura sotto pressione (non linearità geometrica), snervamento plastico (non linearità del materiale) e gradi di libertà di contatto o cinematici. Questi effetti, specialmente per i modelli di materiali non lineari, possono essere considerati utilizzando un metodo di calcolo iterativo.

Impostazione FEM

Passaggi di base per l'impostazione FEM (ulteriori informazioni sono disponibili in [1]):

1. Forma di equilibrio debole
   $${\int }_B\underset{nichtlinearer Anteil}{\underbrace{grad{\delta }_u\cdots \sigma dV}}={\int }_B{\delta }_u·\rho bdV+{\int }_{\partial B}{\delta }_u·t_{o}dA$$

   δu	Spostamento virtuale (di prova)
   t0	Coefficiente iniziale del carico
   σdV	Forze interne
   ρbdV	Forze solide
   B	Area integrata

   Forma debole
2. Conversione alla notazione di Voigt con il tensore 4 Step
   $${\int }_{\mathrm{B}}\mathrm{\delta \epsilon }\cdots \mathrm{ℂ}\cdots \mathrm{\epsilon dV} = {\int }_{\mathrm{B}}\underset{\mathrm{Volumenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}}\mathrm{bdV}}} + {\int }_{\partial \mathrm{B}}\underset{\mathrm{Oberflächenkräfte}}{\underbrace{{\mathrm{\delta u}}^{\mathrm{T}} · {\mathrm{t}}_0\mathrm{dA}}}$$

   C	Matrice di rigidezza
   δε	Variazione dello stato di deformazione
   B	Area integrata
   ε	Deformazione
   U	Spostamento generalizzato

   Formulazione debole nella nota di Voigt
3. Questa notazione è utilizzata nel testo seguente per risolvere la soluzione approssimativa dell'approccio EF per materiali non lineari.
4. Per questo, il campo di spostamento viene moltiplicato per le funzioni di approccio.
   $$\mathrm{u}(\mathrm{x},\mathrm{t}) = \mathrm{H}\left(\mathrm{x}\right)\hat{\mathrm{u}}\left(\mathrm{t}\right)$$

   u(x,t)	Spostamento nel tempo (incremento di carico)
   H	Funzione di forma
   û	Spostamento del nodo

   Campo di spostamento tramite la funzione di prova

Inserimento della derivata dello spostamento nella forma debole. L'integrazione numerica viene utilizzata per calcolare lo spostamento nodale, le tensioni e le deformazioni nella post-elaborazione mediante la regola del materiale.

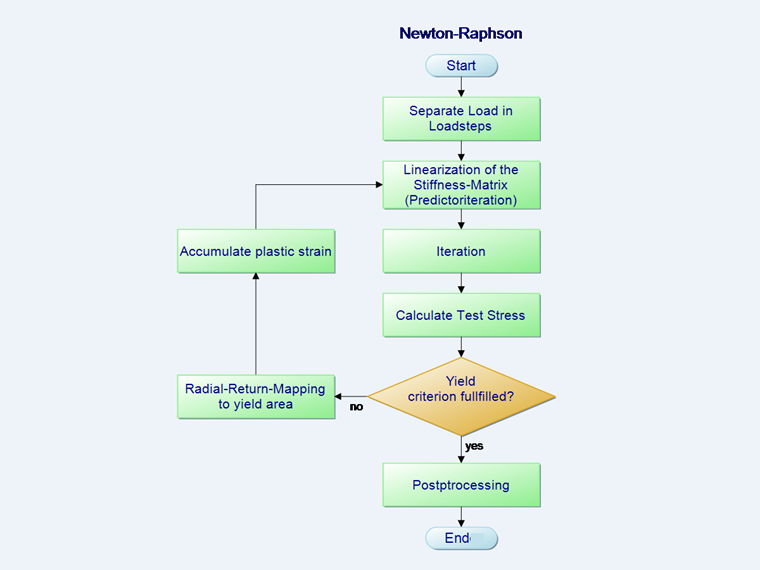
Sequenza di iterazione di Newton-Raphson

A causa del comportamento non lineare del materiale, la matrice del materiale C nell'equazione 2 sopra cambia ad ogni step di espansione. Il metodo di calcolo standard per risolvere questo problema è l'iterazione di Newton-Raphson. Viene utilizzato per linearizzare la funzione in un punto iniziale. La matrice di rigidezza C del passaggio preliminare viene sempre utilizzata nell'iterazione. Nella fase di iterazione linearizzata, una tangente viene posizionata allo zero della funzione.

Le equazioni appartenenti al diagramma di flusso nell'immagine sopra sono le seguenti:

1. Suddivisione del carico in step di carico.
   $${}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} = {}^{\mathrm{t}}\mathrm{f}_{\mathrm{ext}} + ∆\mathrm{f}$$

   fext	Carico esterno
   t	Passo tempo/carico
   Δf	Nuovo incremento di carico

   Carico nelle fasi di carico
2. Passo di predizione
   $${}_0{}^{\mathrm{t}}\mathrm{K}{∆}_0\mathrm{\phi } = {}^{\mathrm{t}+∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_0{}^{\mathrm{t}}\mathrm{f}_{\mathrm{int}}$$

   K	Matrice di rigidezza del time step precedente
   t+Δtfext	Le forze esterne sono aumentate di un ulteriore step di carico
   0tfint	Forze interne del time step precedente
   ϕ	Deformazione

   Passo di predizione
3. Nel punto 3, iterazione del diagramma di flusso, viene calcolata la distorsione totale ridotta dalla distorsione plastica (passo del correttore). L'obiettivo del calcolo iterativo è sempre che la somma dei carichi sia zero. Tuttavia, questo è impossibile numericamente. Pertanto, viene definito un limite di rottura ε al quale il calcolo viene interrotto come sufficientemente accurato.
   $$\mathrm{R} = \left|{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{ext}} - {}_{\mathrm{n}}{}^{\mathrm{t} + ∆\mathrm{t}}\mathrm{f}_{\mathrm{int}}\right| < \mathrm{\epsilon }$$

   R	Limite di interruzione
   fext	Forze esterne
   fint	forze interne
   ε	Limite di interruzione di epsilon
   t	Time step

   Limite di interruzione

Nel programma, il limite di break-off può essere impostato tra i parametri di calcolo.

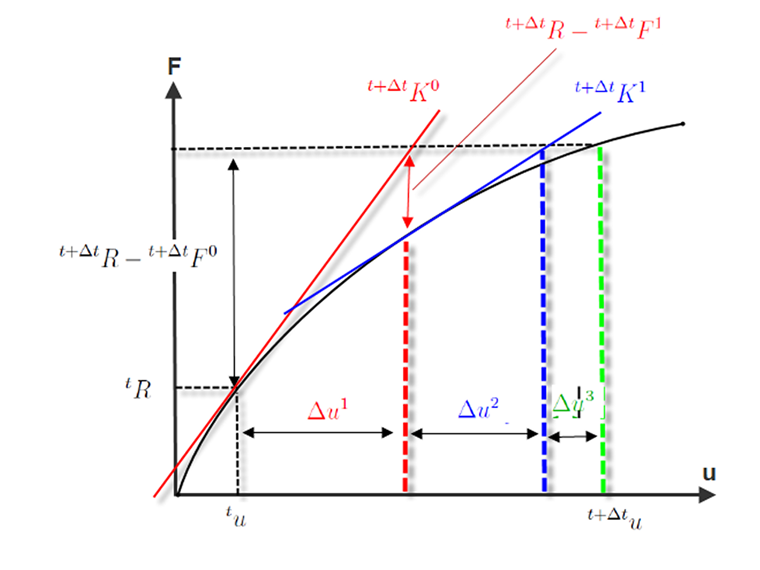
L'immagine seguente mostra il flusso di un'iterazione di Newton-Raphson. Nella prima iterazione

la rottura R o ε non è stata raggiunta. Il limite di tolleranza non viene raggiunto nemmeno nella seconda iterazione (rosso). Solo nella terza iterazione la distanza della rigidezza tangente è così piccola da ottenere la convergenza.

Come già accennato, la deformazione viene sommata continuamente durante l'iterazione.

Conclusione

L'iterazione di Newton-Raphson ha l'ordine di consistenza o di convergenza 2. Il numero di posizioni "corrette" nell'iterazione raddoppia ad ogni passaggio. Pertanto, un'iterazione di Newton-Raphson converge quadraticamente e l'accuratezza aumenta ad ogni iterazione quando il metodo converge. Tuttavia, se il metodo non converge, l'errore diventa infinito e il calcolo viene interrotto.

Le cause dell'errore sono, ad esempio, una pendenza della curva di deformazione del carico che è troppo ripida e un gradiente della curva nell'area plastica che è troppo piatta. Se la curva di deformazione del carico nell'immagine sopra mostrava un'interruzione nella seconda iterazione che era troppo forte, la tangente del materiale e quindi la matrice di rigidezza non visualizzerebbero correttamente la pendenza dell'area elastica. In questo caso, l'inclinazione della radice sarebbe errata per l'area plastica. Questo è uno dei motivi per cui un aumento dei gradini di carico è accompagnato da una migliore convergenza.