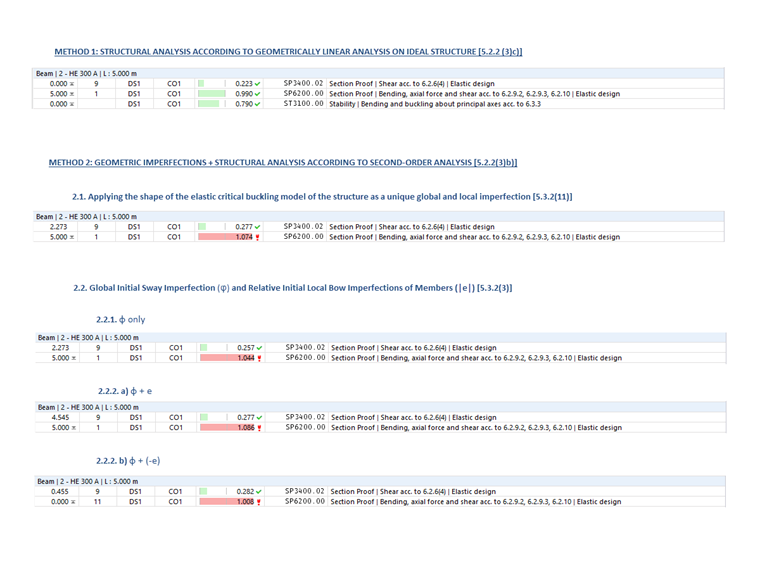
Эта статья базы знаний обсуждает различные методы анализа устойчивости (Изображение 01), предоставленные в EN 1993-1-1:2005 [1], и их применение в программе RFEM 6. Пример, используемый для демонстрации этих методов (Изображение 01), основан на работе Э. Хладнý и М. Штуйберовой [2], предоставленной в конце этой статьи в разделе «Литература». Важно отметить, что в этом примере потеря устойчивости от поперечного изгиба и кручения исключена, и процедура проверки объясняется в следующем абзаце.
В соответствии с вышеупомянутой статьей [1], проверка устойчивости и геометрически линейный анализ конструкции для числового примера представляют первый подход к анализу. Далее обсуждается структурный анализ в соответствии с теорией второго порядка.
В этом случае форма упругого критического режима потеря устойчивости конструкции первоначально вводится как уникальная глобальная и локальная несовершенность. Позднее рассматриваются эквивалентные несовершенства в форме начальной изгибной несовершенности (φ) и отдельных изгибных несовершенств элементов (e). Наконец, результаты анализируются и оцениваются так же, как в [2].
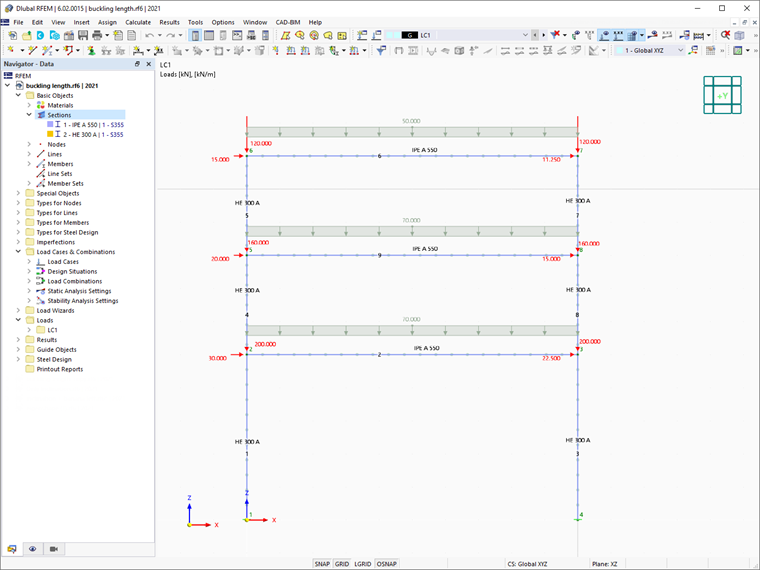
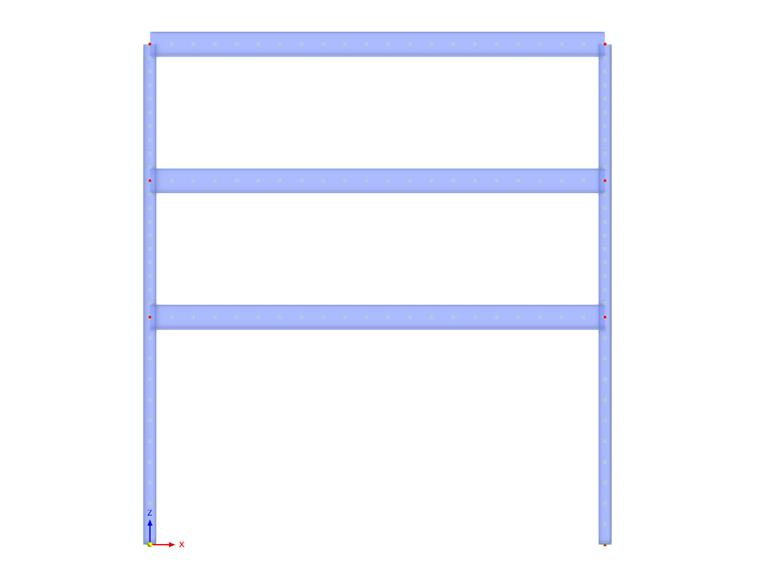
Как уже упоминалось, эти различные методы применяются к численному примеру, и результаты изучаются и сравниваются. Конструкция, представляющая интерес, — это стальная рама, показанная на Изображении 02. Влияния на конструкцию и используемые сечения для балок и колонн также показаны на изображении.
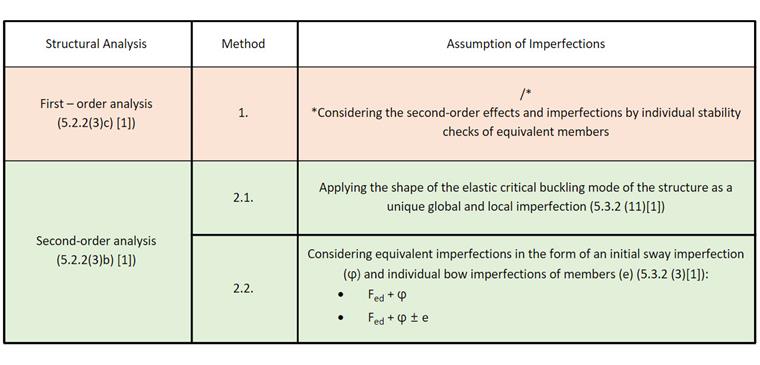
1. Структурный анализ согласно геометрически линейному анализу на идеальной структуре
Метод, указанный в 5.2.2 (3)c) EN 1993-1-1:2005 [1], подразумевает возможность выполнения геометрически линейного анализа и учета эффектов второго порядка и несовершенств путем индивидуальной проверки устойчивости эквивалентных элементов согласно 6.3 [1]. Для этого необходимо использовать соответствующие длины для потери устойчивости в соответствии с глобальным режимом потери устойчивости конструкции, основанным на формате прочности европейских кривых потери устойчивости с коэффициентом уменьшения χ1.
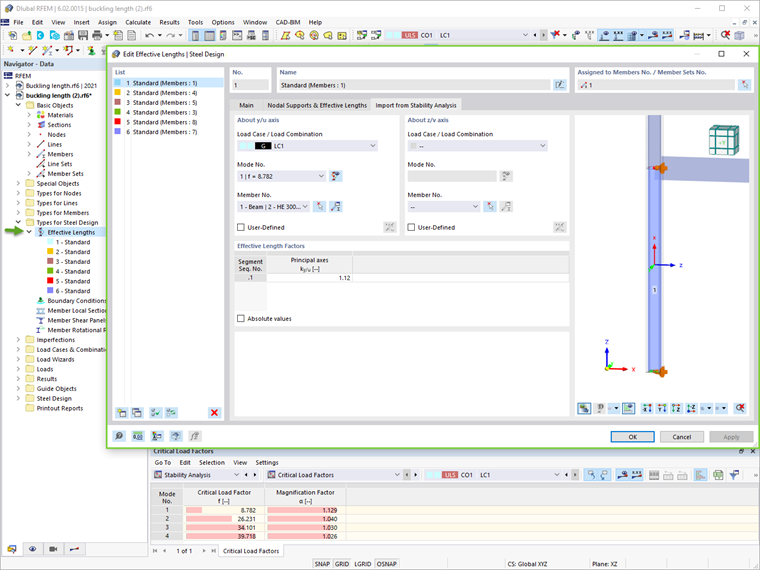
Чтобы сделать это в RFEM 6, убедитесь, что дополнение «Устойчивость конструкции» активировано в дополнение к «Стальному проектированию». Это позволит вам выполнить проверку устойчивости и импортировать эффективные длины из анализа устойчивости (Изображение 03). Больше о этой теме можно найти в статье базы знаний: Определение длины потери устойчивости в RFEM 6 .
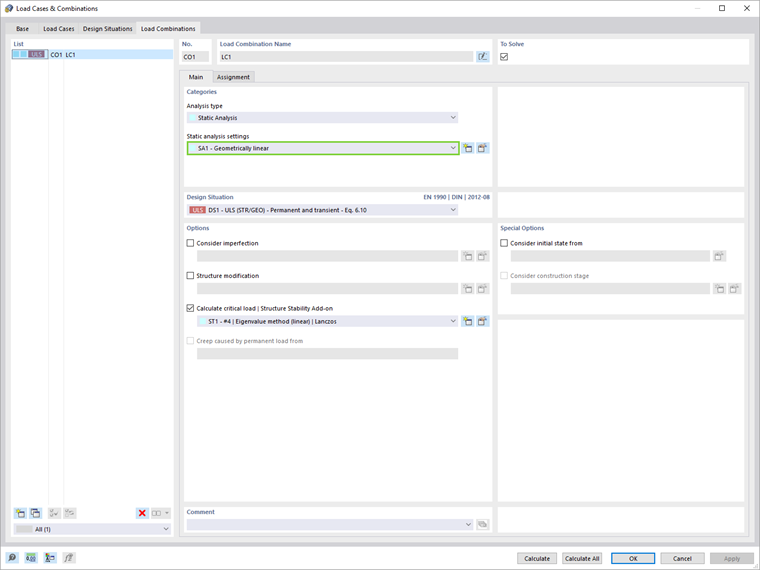
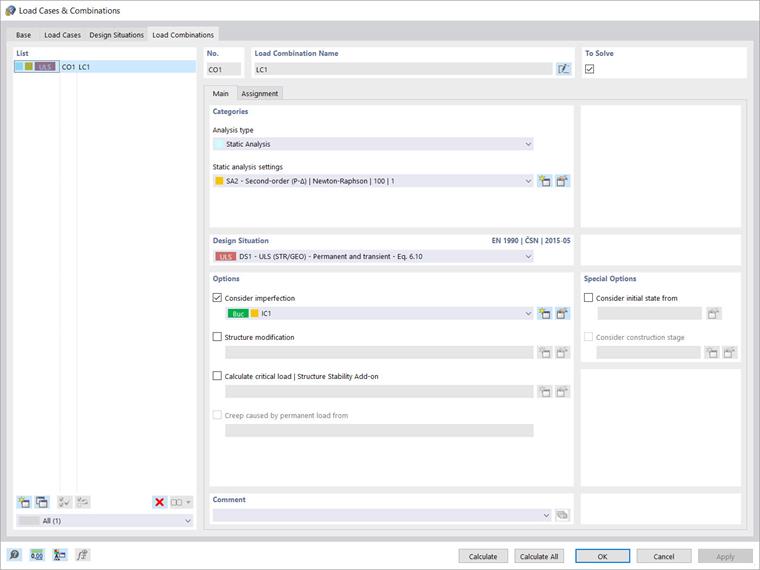
Обратите внимание, что если вы хотите выполнить структурный анализ согласно геометрически линейному анализу, необходимо установить тип анализа «Геометрически линейный» в расчете нагружений и комбинаций (Изображение 04). Таким образом, несовершенства и эффекты второго порядка не учитываются при расчете внутренних сил, а скорее в анализе устойчивости с использованием коэффициента длины для потери устойчивости, обусловленного глобальным поведением рамы.
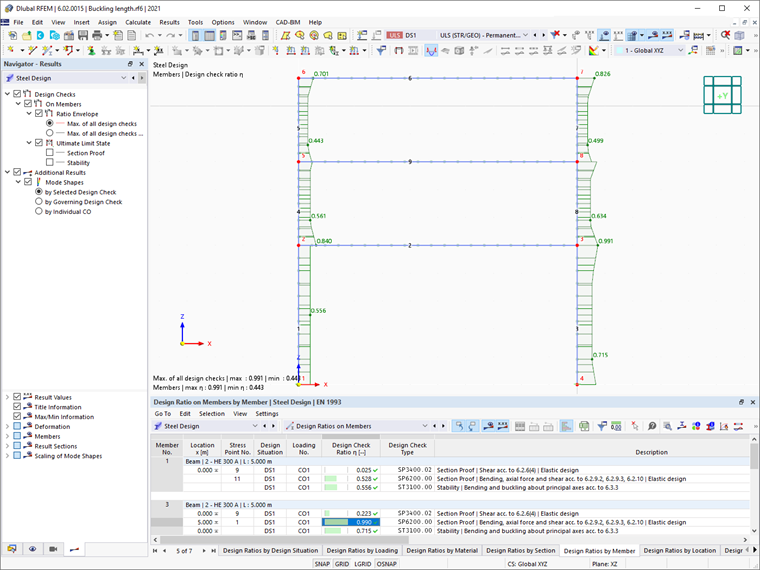
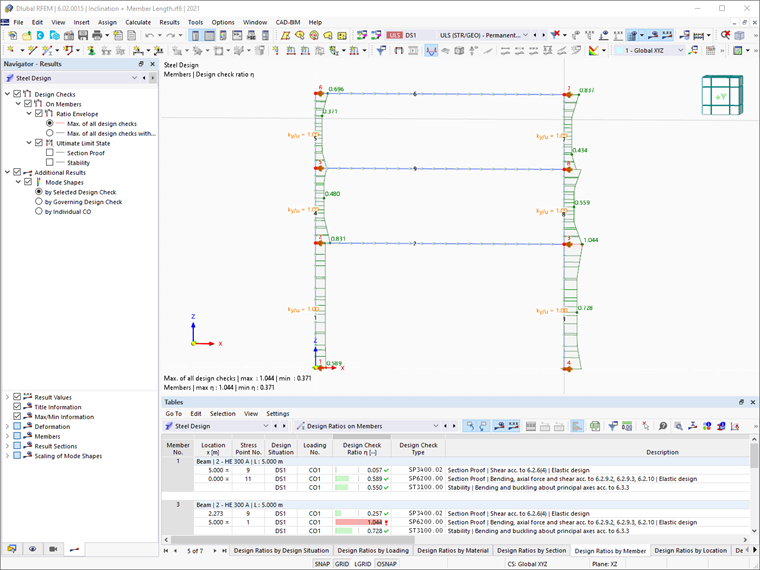
Результаты дополнения «Стальное проектирование» при использовании этого метода показаны на Изображении 05.
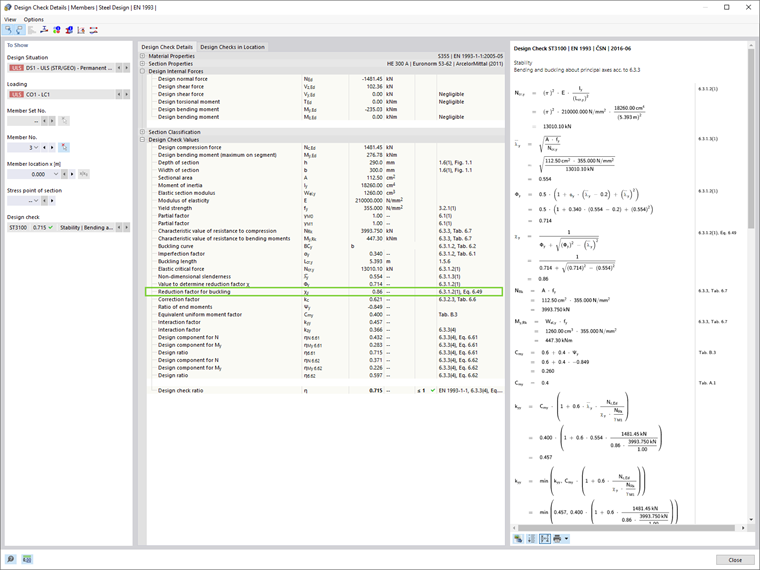
Коэффициент уменьшения для потери устойчивости χ1 в RFEM 6 рассчитываются в соответствии с форматом прочности европейских кривых потери устойчивости. Это можно легко увидеть в деталях проверки отдельных элементов проектирования (Изображение 06), которые можно отобразить, нажав кнопку «Детали проверки проектирования» в таблице результатов стального проектирования.
2. Анализ второго порядка и учет геометрических несовершенств
В общем, критические коэффициенты нагрузки, меньше чем 10, подразумевают, что внутренние силы и моменты должны рассчитываться с учетом эффектов второго порядка. Также необходимо учитывать геометрические несовершенства, и подходы, приведенные в этой статье, следующие:
1. Применение формы упругого критического режима потери устойчивости конструкции как уникальной глобальной и локальной несовершенности (5.3.2.11 [1]) 2. Учет эквивалентных несовершенств в форме начальной изгибной несовершенности и отдельных изгибных несовершенств элементов (5.3.2.3 [1])
2.1. Применение формы упругого критического режима потери устойчивости конструкции как уникальной глобальной и локальной несовершенности
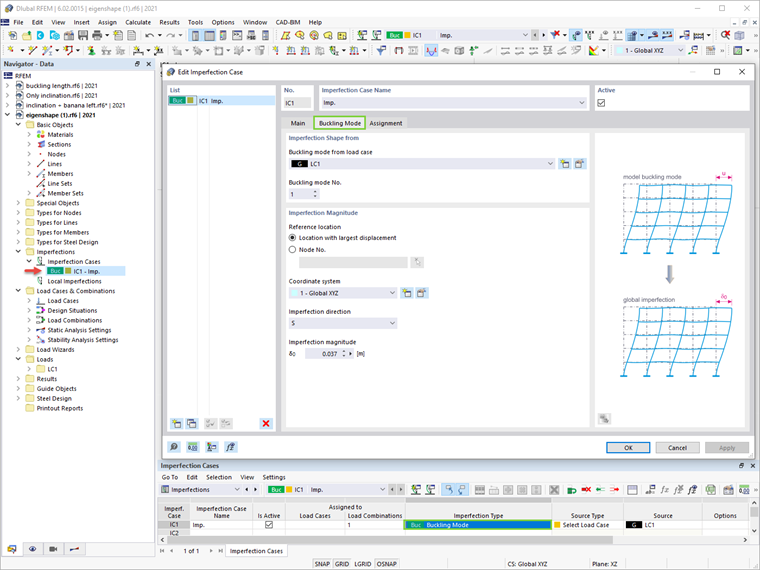
Подход, предложенный в 5.3.2.11 [1], предполагает, что форма упругого критического режима потери устойчивости конструкции может быть применена как уникальная глобальная и локальная несовершенность. Для этого в RFEM 6 необходимо создать случай несовершенства с типом несовершенства «Режим потери устойчивости».
Первый режим потери устойчивости конструкции был рассчитан в анализе устойчивости, описанном в предыдущей главе, и теперь его можно использовать для определения случая несовершенства, как показано на Изображении 07. Настройки анализа второго порядка, касающиеся эффектов несовершенства в форме режима потери устойчивости, показаны на Изображении 08.
2.2. Учет эквивалентных несовершенств в форме начальной изгибной несовершенности (φ) и отдельных изгибных несовершенств элементов (e)
Согласно подходу, представленному в 5.3.2 (3) [1], эффект несовершенств для рам, подверженных потере устойчивости в форме изгиба, должен применяться в анализе рамы с использованием эквивалентной несовершенности в форме начальной изгибной несовершенности и отдельных изгибных несовершенств элементов.
2.2.1. Начальная изгибная несовершенность (φ)
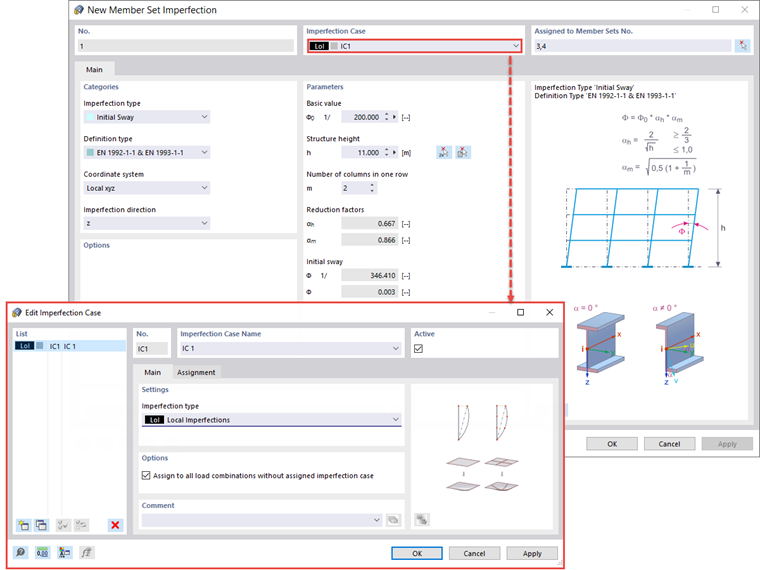
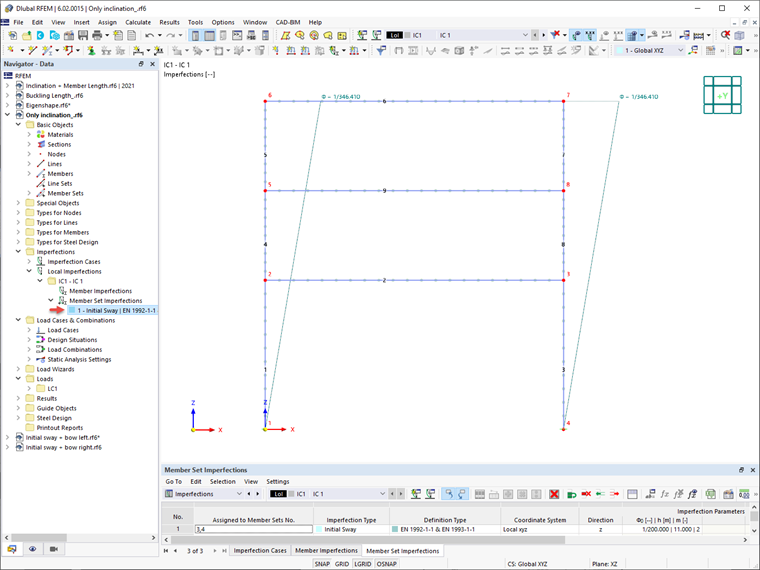
Сначала анализ будет проведен с учетом эквивалентной несовершенности в форме только начальной изгибной несовершенности. В RFEM 6 глобальная начальная изгибная несовершенность вводится как «Несовершенность комплекта элементов», как показано на Изображении 09.
Таким образом, начальная изгибная несовершенность определена, как показано на Изображении 10.
2.2.2. Начальная изгибная несовершенность (φ) и отдельные изгибные несовершенности элементов (±e)
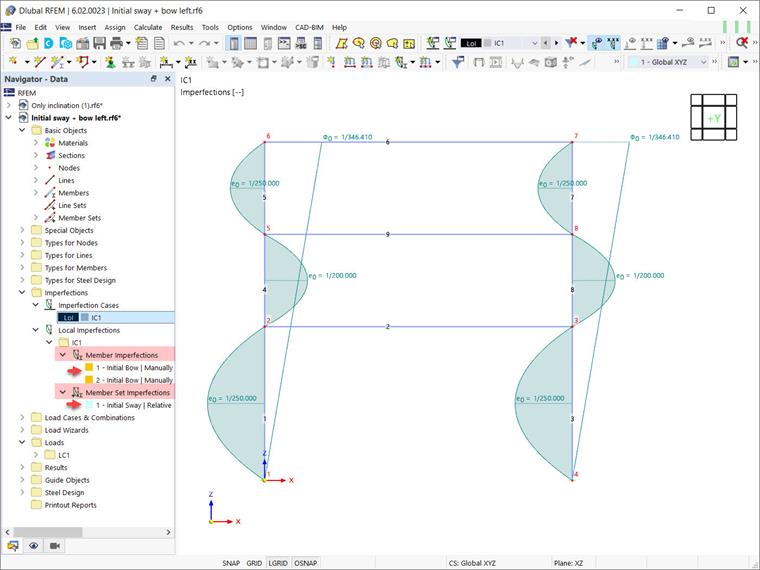
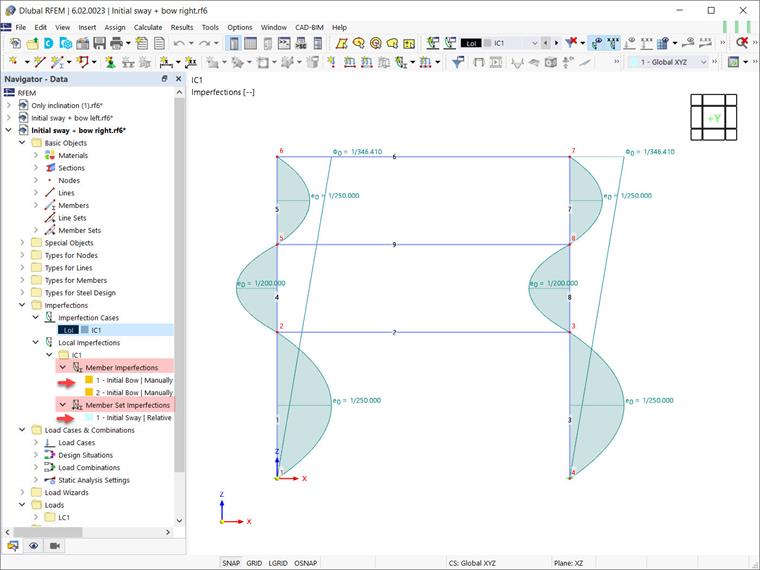
Помимо глобальных изгибных несовершенств, необходимо учитывать относительные начальные локальные изгибные несовершенства элементов. В RFEM 6 они могут быть определены как несовершенства элементов с типом «Начальный изгиб». В этом примере такие несовершенства рассматриваются один раз для положительного глобального направления X (+e) и один раз для отрицательного направления (-e). Это показано на Изображениях 11 и 12 соответственно.
Сводка результатов
Сравнение различных методов (Изображение 13) приводит к выводу, что использование формата прочности европейских кривых потери устойчивости с коэффициентом уменьшения χ1 (Метод 1) дает менее консервативные результаты, чем метод прямого проектирования (Метод 2), который учитывает несовершенства и структурный анализ в соответствии с теорией второго порядка. Результаты также показывают, что различия между обоими подходами, учитывающими эффекты несовершенства в Методе 2 (то есть 5.3.2(3) и 5.3.2(11)), довольно малы для прямоугольных непрерывных рам.
В этот момент мы можем сослаться на 5.3.2 (6) EN 1993-1-1:2005 [1], который предполагает, что локальные изгибные несовершенства могут быть проигнорированы при выполнении глобального анализа для определения конечных сил и моментов, которые будут использоваться в проверках элементов согласно 6.3.
Таким образом, несовершенства могут быть введены только в форме глобальной изгибной несовершенности в этом числовом примере, и проверки устойчивости эквивалентных элементов согласно 6.3 [1] могут быть выполнены. Учитывая анализ второго порядка и учет глобального поведения рамы, эта проверка должна основываться на длине для потери устойчивости, равной длине элемента, как это предусмотрено в 5.2.2 (7) b EN 1993-1-1:2005 [1]. Наконец, результаты показаны на Изображении 14.