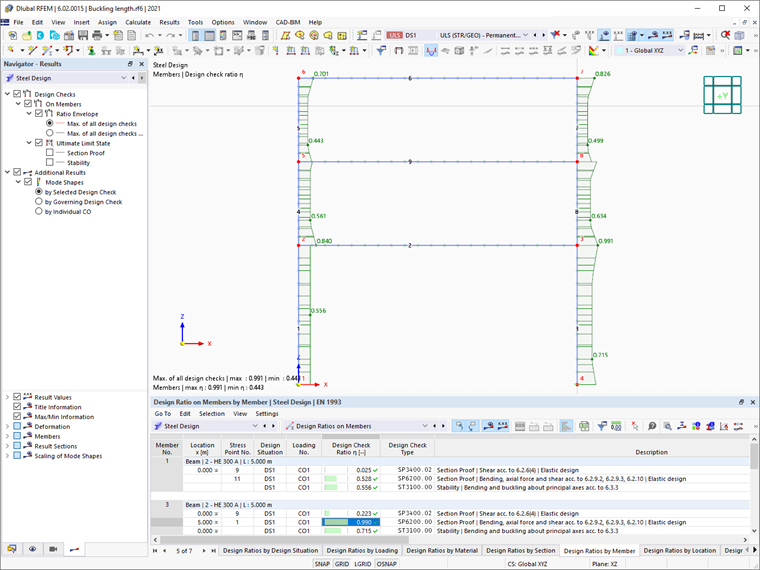
Tento článek vědomostní báze diskutuje různé metody pro analýzu stability (Obrázek 01) dle EN 1993-1-1:2005 [1] a jejich aplikaci v programu RFEM 6. Příklad použitý k demonstraci těchto metod (Obrázek 01) je založen na práci E. Chladnýho a M. Štujberové [2] uvedené na konci tohoto článku pod „Reference“. Je důležité si uvědomit, že v tomto příkladu je vynecháno klopení, a ověřovací postup je vysvětlen v následujícím odstavci.
V souladu s výše uvedeným článkem [1] se jako první přístup analýzy považuje kontrola stability a geometricky lineární statická analýza pro numerický příklad zájmu. Následně se diskutuje statická analýza podle druhého řádu.
V tomto případě je tvar elastického kritického tvaru vzpěru konstrukce nejprve zaveden jako unikátní globální a lokální počáteční deformace. Později jsou uvažovány ekvivalentní počáteční deformace ve formě počátečního vychýlení (φ) a jednotlivých vychýlení členů (e). Nakonec jsou výsledky analyzovány a hodnoceny stejným způsobem jako v [2].
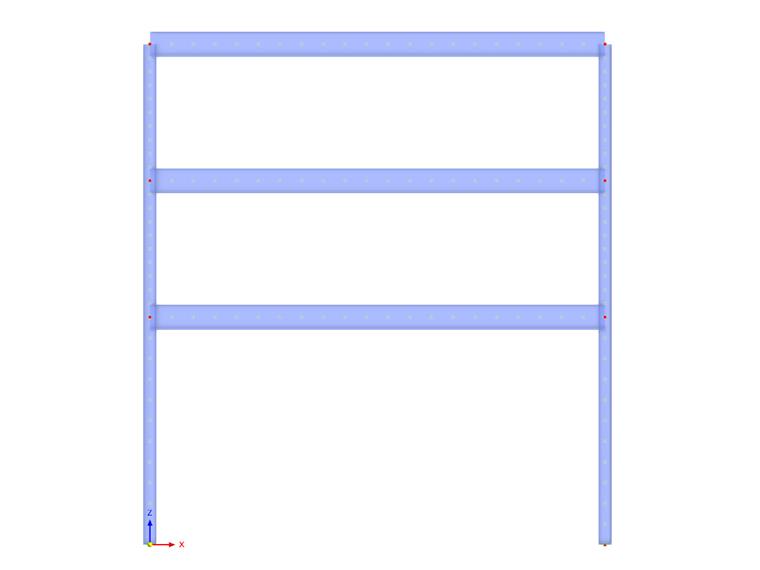
Jak již bylo zmíněno, tyto různé metody jsou aplikovány na numerický příklad a výsledky jsou zkoumány a porovnávány. Konstrukce zájmů je ocelový rám znázorněný na obrázku 02. Působení na konstrukci a průřezy použité pro nosníky a sloupy jsou také zobrazeny na obrázku.
1. Statická analýza podle geometricky lineární analýzy na ideální konstrukci
Metoda uvedená v 5.2.2 (3)c) EN 1993-1-1:2005 [1] naznačuje, že je možné provést geometricky lineární analýzu a uvažovat účinky druhého řádu a počáteční deformace individuálními stabilitními kontrolami ekvivalentních členů podle 6.3 [1]. Pro tento účel je nutné použít vhodné vzpěrné délky v souladu s globálním módním vzpěrem konstrukce, na základě formátu pevnosti evropských vzpěrných křivek s redukčním faktorem χ1.
Pro provedení tohoto v RFEM 6 se ujistěte, že je aktivován doplněk „Stabilita konstrukce“ kromě doplňku „Ocelový návrh“. To vám umožní provádět stabilitní kontrolu a importovat efektivní délky ze stabilitní analýzy (Obrázek 03). Více o tomto tématu naleznete v článku vědomostní báze: Stanovení vzpěrných délek v programu RFEM 6 .
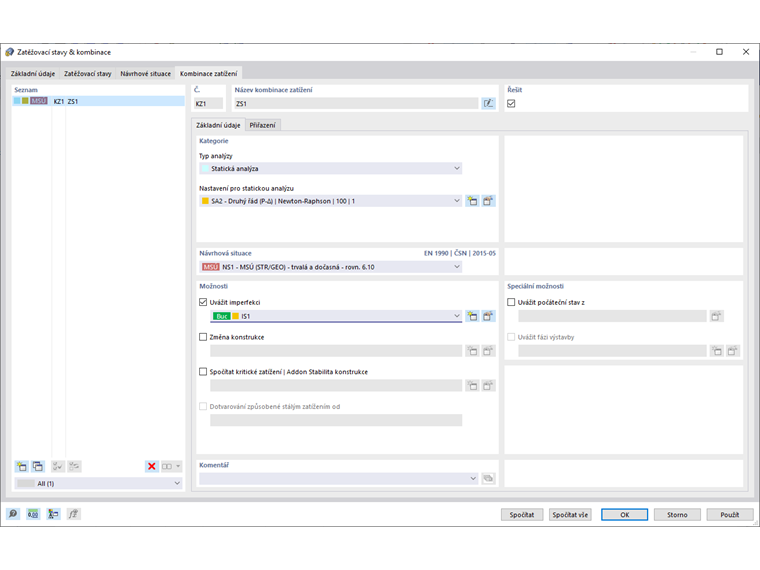
Vezměte na vědomí, že pokud chcete provést statickou analýzu podle geometricky lineární analýzy, je nutné nastavit typ analýzy „Geometricky lineární“ v zatěžovacích případech a kombinacích, které mají být vypočítány (Obrázek 04). Tímto způsobem nejsou počáteční deformace a účinky druhého řádu uvažovány ve výpočtu vnitřních sil, ale spíše ve stabilitní analýze pomocí faktoru pro vzpěrnou délku vzhledem k globálnímu chování rámu.
Výsledky doplňku „Ocelový návrh“ použitím této metody jsou zobrazeny na obrázku 05.
Redukční faktor pro vzpěr χ1 v RFEM 6 je vypočten v souladu s formátem pevnosti evropských vzpěrných křivek. To je snadno viditelné v detailech návrhové kontroly jednotlivých členů (Obrázek 06), které lze zobrazit kliknutím na tlačítko „Detaily návrhové kontroly“ v tabulce výsledků ocelových návrhů.
2. Analýza druhého řádu a zohlednění geometrických počátečních deformací
Obecně platí, že u kritických zatěžovacích faktorů nižších než 10 by měly být vnitřní síly a momenty počítány s ohledem na účinky druhého řádu. Geometrické počáteční deformace by také měly být zvažovány a přístupy prezentované v tomto článku jsou následující:
- Aplikace tvaru elastického kritického vzpěrného tvaru konstrukce jako unikátní globální a lokální počáteční deformace (5.3.2.11 [1])
- Zohlednění ekvivalentních počátečních deformací ve formě počátečního vychýlení a jednotlivých vychýlení členů (5.3.2.3 [1])
2.1. Aplikace tvaru elastického kritického vzpěrného tvaru konstrukce jako unikátní globální a lokální počáteční deformace
Přístup uvedený v 5.3.2.11 [1] navrhuje, že tvar elastického kritického vzpěrného tvaru konstrukce může být aplikován jako unikátní globální a lokální počáteční deformace. K provedení tohoto v RFEM 6 je nutné vytvořit případ počáteční deformace s typem „Tvar vzpěru“.
První tvar vzpěru konstrukce byl vypočítán ve stabilitní analýze popsáné v předchozí kapitole, a nyní může být použit k definici případu počáteční deformace, jak je ukázáno na Obrázku 07. Nastavení analýzy druhého řádu týkající se účinků počáteční deformace v tvaru vzpěru jsou ukázána na Obrázku 08.
2.2. Zohlednění ekvivalentních počátečních deformací ve formě počátečního vychýlení (φ) a jednotlivých vychýlení členů (e)
Podle přístupu prezentovaného v 5.3.2 (3)[1] by měl být pro rámy náchylné k vychýlení vliv počátečních deformací aplikován v analýze rámu s použitím ekvivalentní počáteční deformace ve formě počátečního vychýlení a jednotlivých vychýlení členů.
2.2.1. Počáteční vychýlení (φ)
Nejprve bude analýza provedena s ohledem na ekvivalentní počáteční deformaci ve formě pouze počátečního vychýlení. V RFEM 6 je globální počáteční vychýlení zavedeno jako „Počáteční deformace sady členů“, jak je zobrazeno na Obrázku 09.
Tímto způsobem je počáteční vychýlení definováno, jak je ukázáno na Obrázku 10.
2.2.2. Počáteční vychýlení (φ) a jednotlivé vychýlení členů (±e)
Kromě globálních vychýlení by měly být zváženy místní počáteční vychýlení členů. V RFEM 6 mohou být definována jako počáteční deformace členů s typem „Počáteční vychýlení“. V tomto příkladě jsou takové počáteční deformace zvažovány jednou pro pozitivní globální směr X (+e) a jednou pro negativní směr (-e). To je ukázáno na Obrázcích 11 a 12, respektive.
Shrnutí výsledků
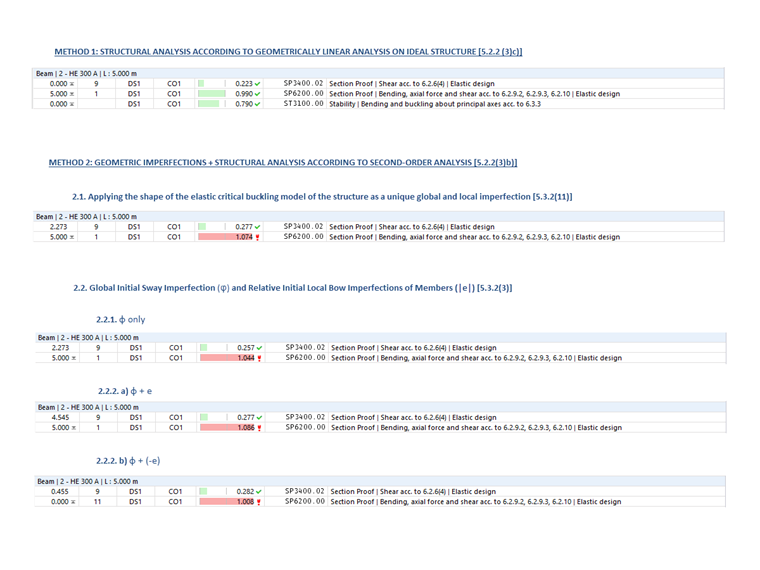
Srovnání různých metod (Obrázek 13) vede k závěru, že použití formátu pevnosti evropských vzpěrných křivek s redukčním faktorem χ1 (Metoda 1) dává méně konzervativní výsledky než přímá návrhová metoda (Metoda 2), která zahrnuje počáteční deformace a statickou analýzu podle teorie druhého řádu. Výsledky také ukazují, že rozdíly mezi oběma přístupy zohledňujícími účinky počátečních deformací v Metodě 2 (to jest 5.3.2(3) a 5.3.2(11)) jsou spíše malé pro obdélníkové průběžné rámy.
Na tomto místě můžeme odkázat na 5.3.2 (6) EN 1993-1-1:2005 [1], který naznačuje, že místní vychýlení mohou být zanedbána při provádění globální analýzy pro určení koncových sil a koncových momentů, které mají být použity při kontrolách členů podle 6.3.
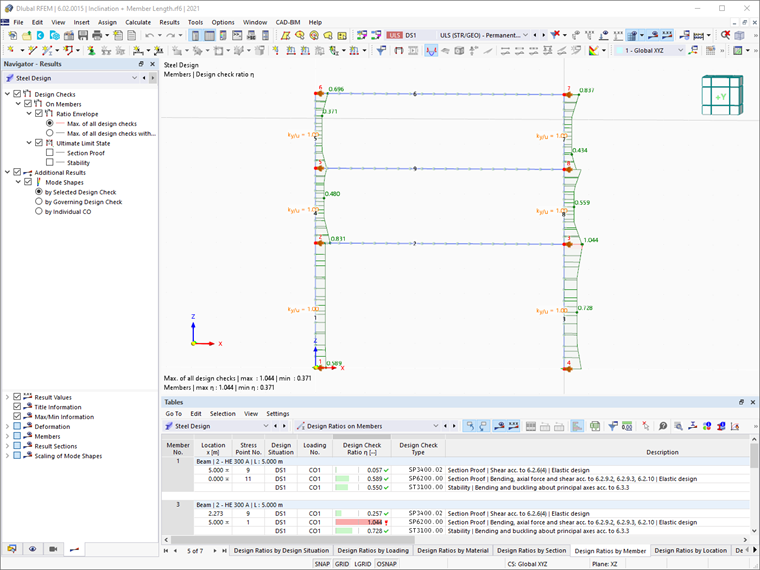
Tak mohou být v tomto numerickém příkladu počáteční deformace zavedeny pouze ve formě globálního vychýlení a mohou být provedeny stabilitní kontroly ekvivalentních členů podle 6.3 [1]. Vzhledem k analýze druhého řádu a zohlednění globálního chování rámu by toto ověření mělo být založeno na vzpěrné délce rovné délce členu, jak je uvedeno v 5.2.2 (7) b EN 1993-1-1:2005 [1]. Nakonec jsou výsledky zobrazeny na Obrázku 14.