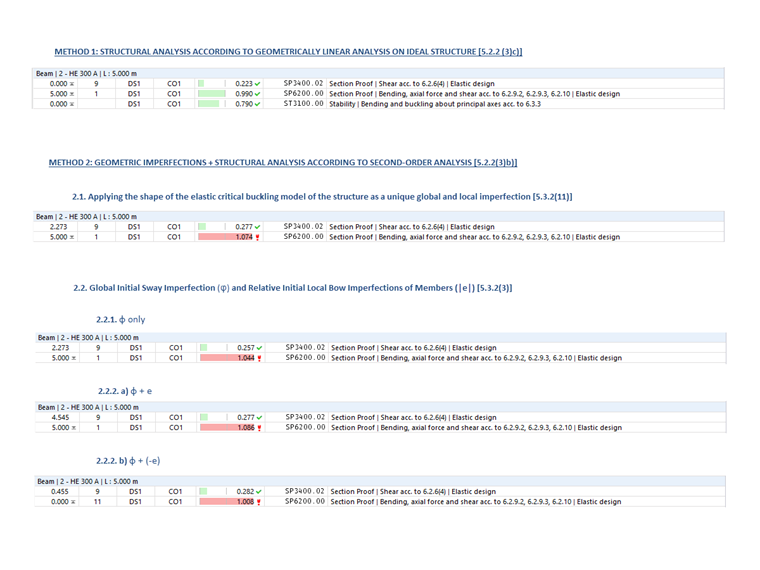
Ten artykuł z Bazy Wiedzy omawia różne metody analizy stateczności (Obraz 01) przedstawione w EN 1993-1-1:2005 [1] oraz ich zastosowanie w programie RFEM 6. Przykład użyty do zilustrowania tych metod (Obraz 01) oparty jest na pracy E. Chladný i M. Štujberová [2] podanej na końcu tego artykułu w sekcji „Referencje”. Ważne jest zaznaczenie, że wyboczenie skrętne jest wyłączone w tym przykładzie, a procedura weryfikacyjna jest wyjaśniona w poniższym akapicie.
Zgodnie z wyżej wspomnianym artykułem [1], jako pierwsze podejście do analizy rozważane są sprawdzenie projektowe stateczności i geometria analizy liniowej strukturalnej dla interesującego przykładu numerycznego. Następnie omawiana jest analiza strukturalna według analizy drugiego rzędu.
W tym przypadku, kształt krytycznego wyboczenia struktury jest najpierw wprowadzany jako unikalna globalna i lokalna imperfekcja. Później rozważane są równoważne imperfekcje w formie początkowej imperfekcji przechyłu (φ) oraz indywidualnych imperfekcji wygięcia elementów (e). Na końcu, wyniki są analizowane i oceniane w taki sam sposób jak w [2].
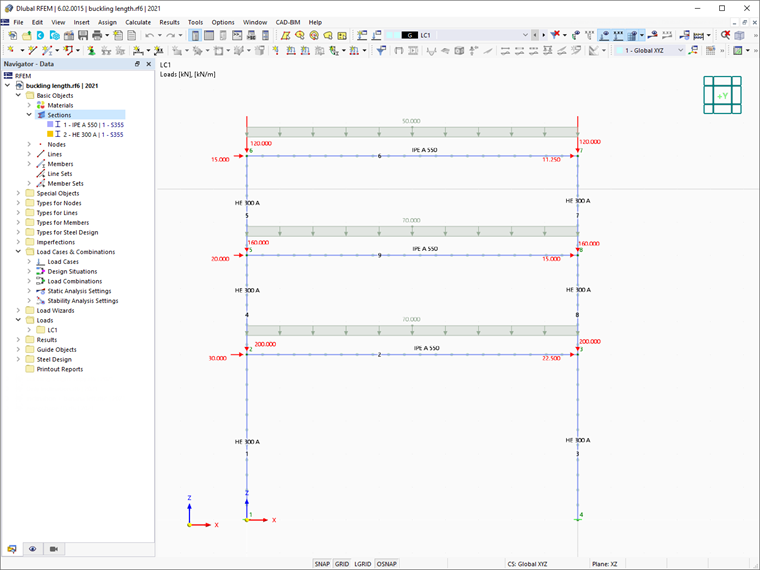
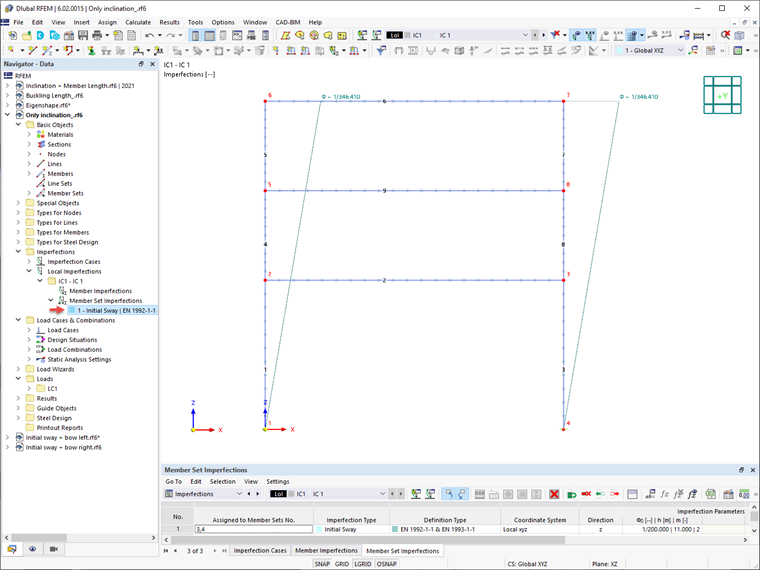
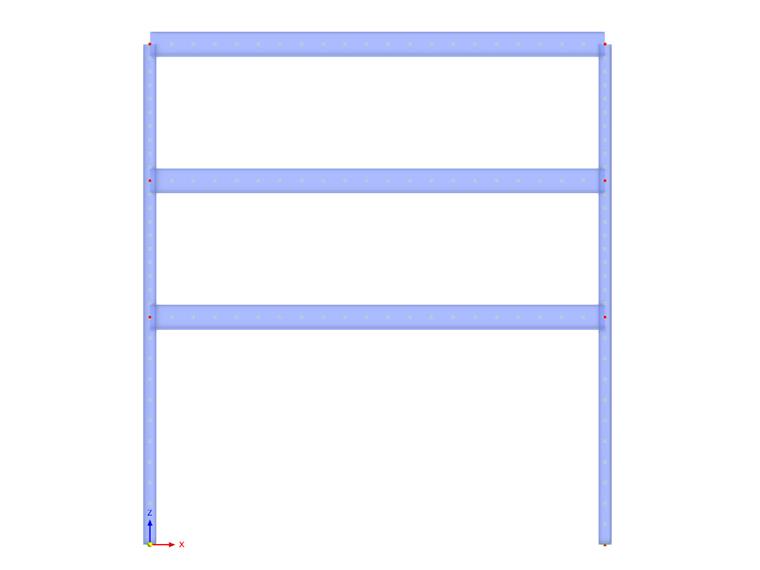
Jak już wspomniano, różne metody są stosowane do przykładu numerycznego, a wyniki są badane i porównywane. Interesująca struktura to stalowa rama pokazana na Obrazie 02. Obciążenia działające na strukturę oraz przekroje użyte dla belek i słupów także ukazane są na obrazie.
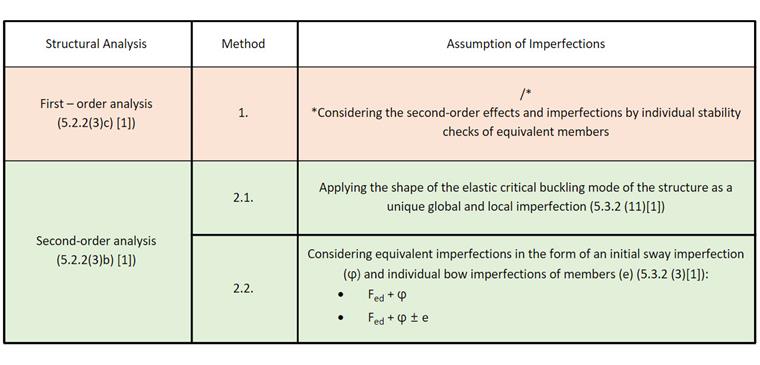
1. Analiza Strukturalna według Geometrieowo Liniowej Analizy na Struktury Idealnej
Metoda podana w 5.2.2 (3)c) EN 1993-1-1:2005 [1] sugeruje, że możliwe jest przeprowadzenie analizy geometrii liniowej oraz rozważenie efektów drugiego rzędu i imperfekcji poprzez indywidualne sprawdzenie stateczności równoważnych elementów według 6.3 [1]. Do tego celu konieczne jest użycie odpowiednich długości wyboczeniowych zgodnych z globalnym trybem wyboczenia struktury, opartych na formacie wytrzymałości europejskich krzywych wyboczeniowych z współczynnikiem redukcji χ1.
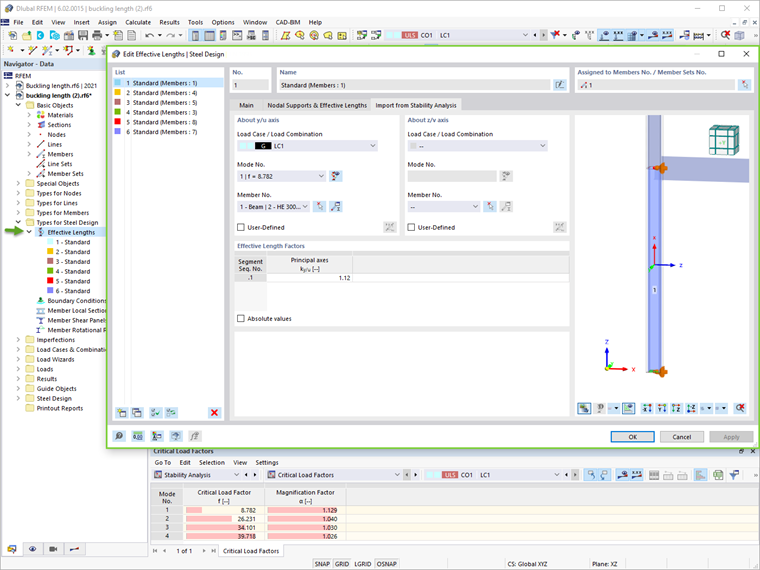
Aby to zrobić w RFEM 6, upewnij się, że dodatek "Stabilność Struktury" jest aktywowany, oprócz dodatku "Projektowanie Stali". Umożliwi to wykonanie sprawdzenia stateczności i import efektywnych długości z analizy stateczności (Obraz 03). Więcej o tym temacie można znaleźć w artykule z Bazy Wiedzy: Definiowanie długości efektywnych w RFEM 6 .
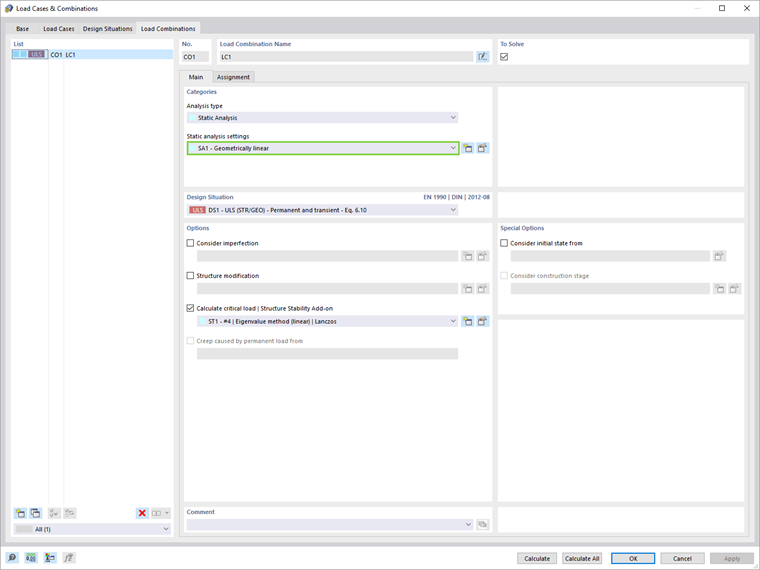
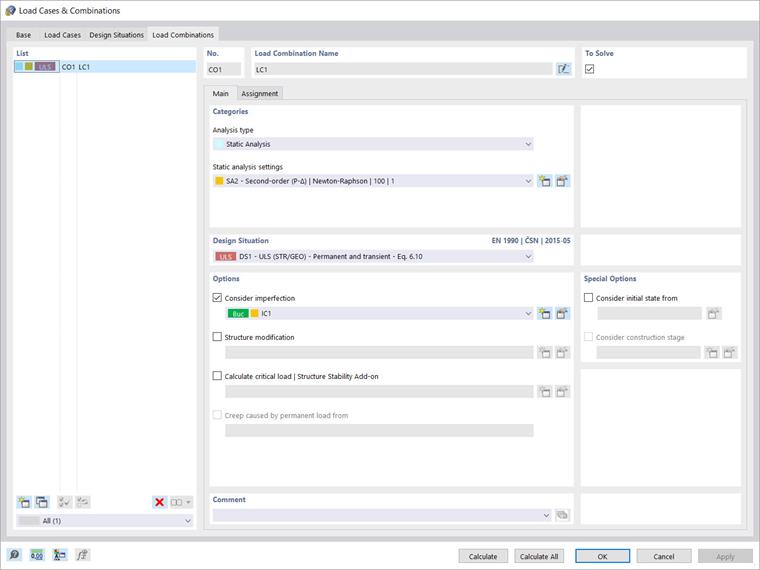
Należy pamiętać, że jeśli chcesz przeprowadzić analizę strukturalną zgodnie z analizą geometrii liniowej, konieczne jest ustawienie typu analizy „linia geometrii” w przypadkach obliczeniowych i kombinacjach do obliczenia (Obraz 04). W ten sposób imperfekcje i efekty drugiego rzędu nie są rozważane w obliczaniu sił wewnętrznych, ale raczej w analizie stateczności z użyciem współczynnika długości wyboczeniowej ze względu na globalne zachowanie ramy.
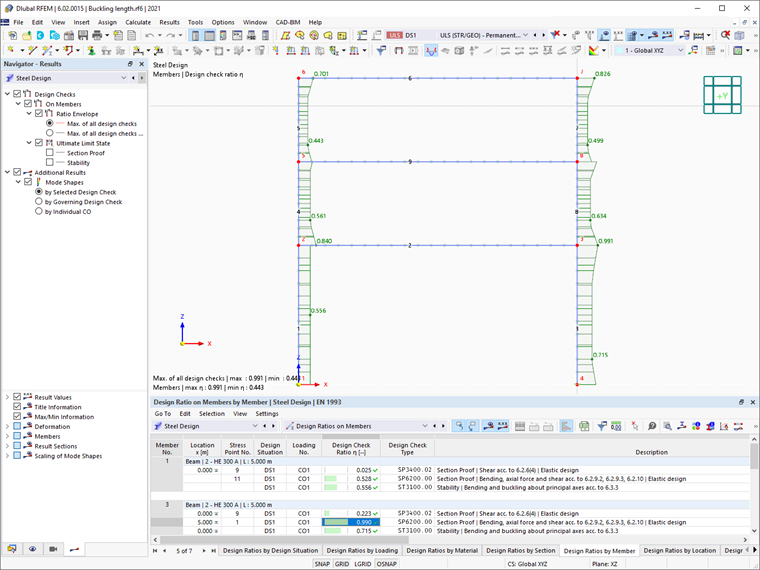
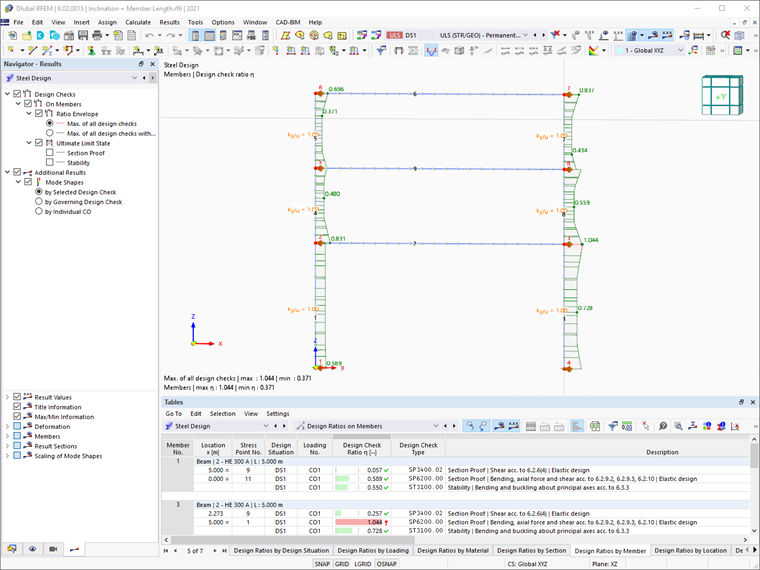
Wyniki dodatku "Projektowanie Stali" przy użyciu tej metody pokazane są na Obrazie 05.
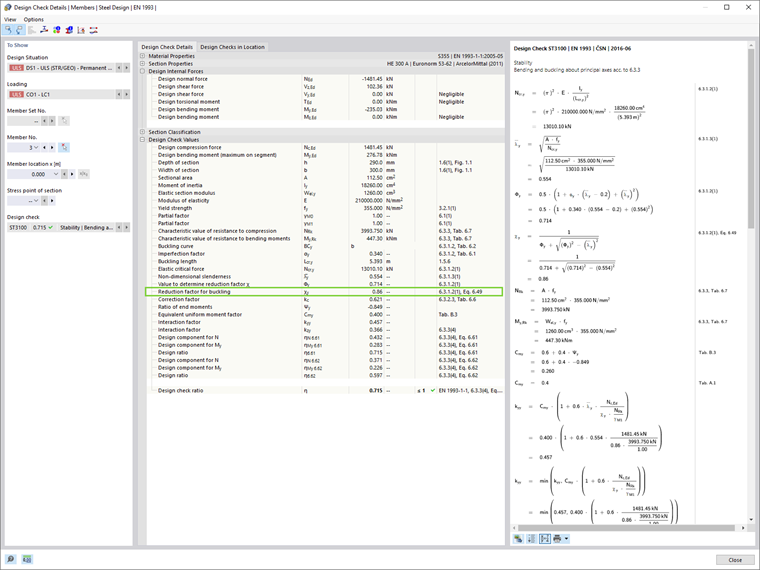
W RFEM 6 współczynnik redukcji wyboczenia χ1 jest obliczany zgodnie z formatem wytrzymałości europejskich krzywych wyboczeniowych. Można to łatwo zobaczyć w szczegółach sprawdzenia projektowego poszczególnych elementów (Obraz 06), które można wyświetlić klikając przycisk „Szczegóły sprawdzenia projektowego” w tabeli wyników Projektowania Stali.
2. Analiza Drugiego Rzędu i Rozważenie Imperfekcji Geometrycznych
Ogólnie, współczynniki krytycznych obciążeń mniejsze niż 10 sugerują, że siły wewnętrzne i momenty powinny być obliczone z uwzględnieniem efektów drugiego rzędu. Należy także rozważyć imperfekcje geometryczne, a metody przedstawione w tym artykule są następujące:
1. Zastosowanie kształtu elastycznego krytycznego trybu wyboczenia struktury jako unikalnej globalnej i lokalnej imperfekcji (5.3.2.11 [1]) 2. Rozważenie równoważnych imperfekcji w formie początkowej imperfekcji przechyłu i indywidualnych imperfekcji wygięcia elementów (5.3.2.3 [1])
2.1. Zastosowanie Kształtu Elastycznego Krytycznego Trybu Wyboczenia Struktury jako Unikalnej Globalnej i Lokalnej Imperfekcji
Podejście wprowadzone w 5.3.2.11 [1] sugeruje, że kształt elastycznego krytycznego trybu wyboczenia struktury może być zastosowany jako unikalna globalna i lokalna imperfekcja. Aby to zrobić w RFEM 6, konieczne jest stworzenie przypadku imperfekcji z typem imperfekcji „Tryb Wyboczenia”.
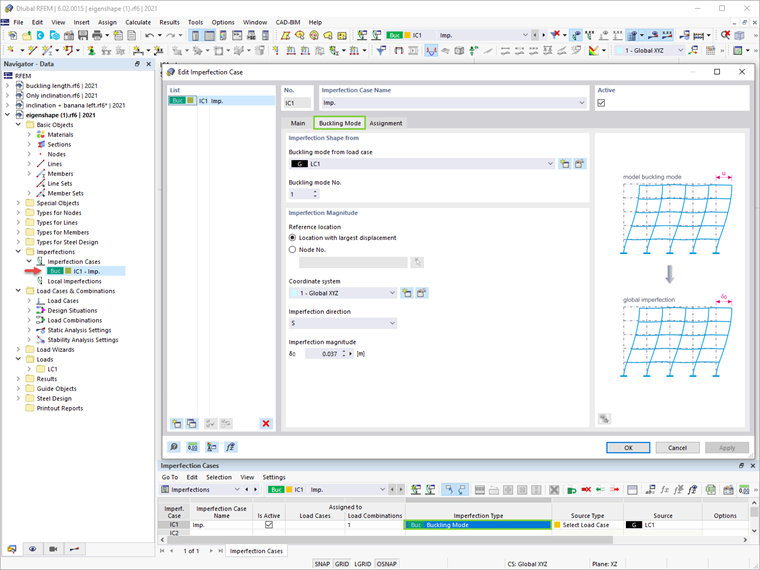
Pierwszy tryb wyboczenia struktury został obliczony w analizie stateczności opisanej w poprzednim rozdziale i można go teraz użyć do definiowania przypadku imperfekcji, jak pokazano na Obrazie 07. Ustawienia analizy drugiego rzędu dotyczące efektów imperfekcji w kształcie trybu wyboczenia pokazane są na Obrazie 08.
2.2. Rozważenie Równoważnych Imperfekcji w Formie Początkowej Imperfekcji Przechyłu (φ) i Indywidualnych Imperfekcji Wygięcia Elementów (e)
Zgodnie z podejściem przedstawionym w 5.3.2 (3)[1], efekt imperfekcji dla ram podatnych na wyboczenie w trybie przechyłu powinien być zastosowany w analizie ram, używając równoważnej imperfekcji w formie początkowej imperfekcji przechyłu i indywidualnych imperfekcji wygięcia elementów.
2.2.1. Początkowa Imperfekcja Przechyłu (φ)
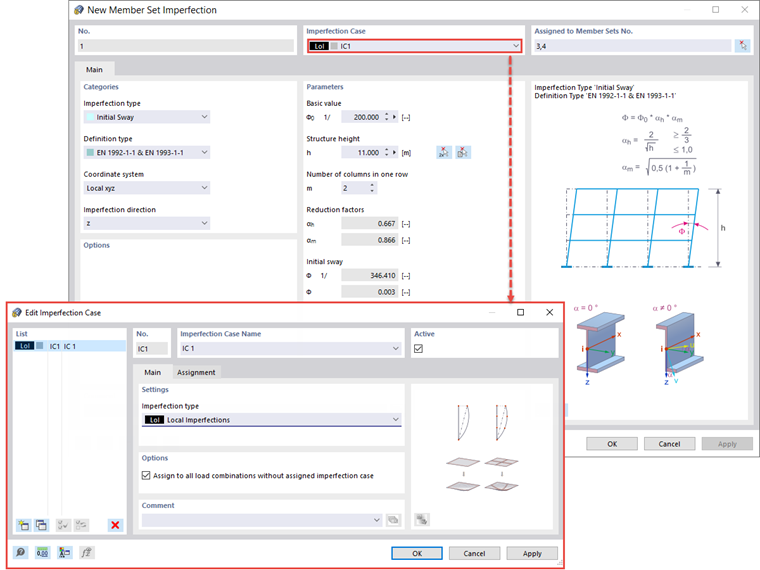
Na początek analiza zostanie przeprowadzona przy rozważeniu równoważnej imperfekcji w formie tylko początkowej imperfekcji przechyłu. W RFEM 6 globalna początkowa imperfekcja przechyłu jest wprowadzana jako "Imperfekcja Zestawów Elementów", jak pokazano na Obrazie 09.
W ten sposób początkowy przechył jest zdefiniowany, jak pokazano na Obrazie 10.
2.2.2. Początkowa Imperfekcja Przechyłu (φ) i Indywidualne Imperfekcje Wygięcia Elementów (±e)
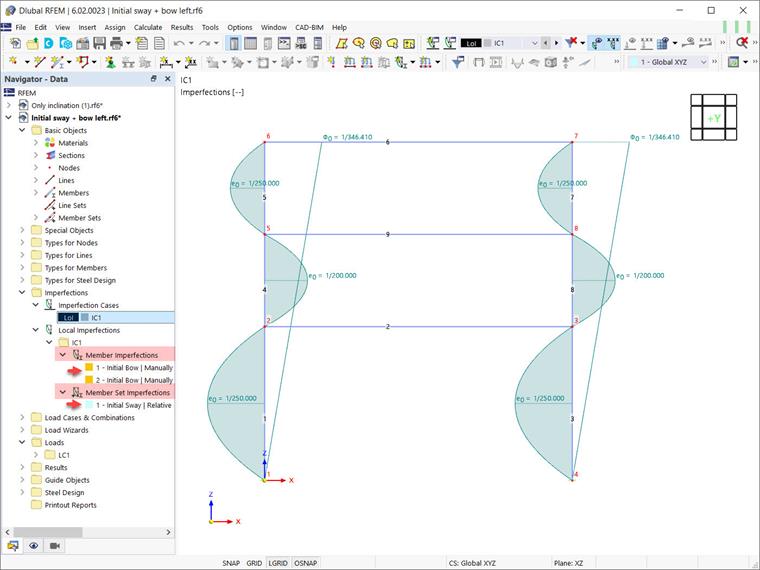
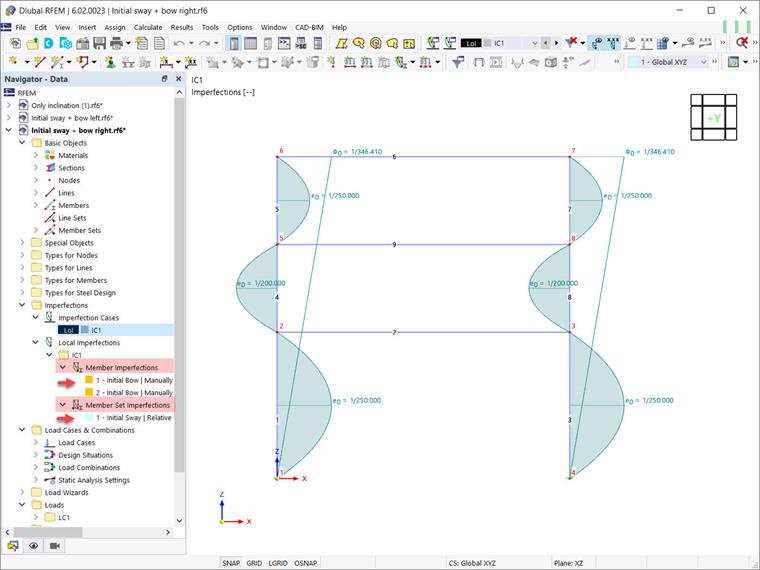
Oprócz globalnych imperfekcji przechyłu, należy rozważyć względne lokalne imperfekcje wygięcia elementów. W RFEM 6 mogą być one zdefiniowane jako imperfekcje elementów z typem „Początkowe Wygięcie”. W tym przykładzie takie imperfekcje są rozważane raz dla globalnego pozytywnego kierunku X (+e), i raz dla kierunku negatywnego (-e). Jest to pokazane odpowiednio na Obrazach 11 i 12.
Podsumowanie Wyników
Porównanie różnych metod (Obraz 13) prowadzi do wniosku, że użycie formatu wytrzymałości europejskich krzywych wyboczeniowych z współczynnikiem redukcji χ1 (Metoda 1) daje mniej konserwatywne wyniki w porównaniu do metody projektowej bezpośredniej (Metoda 2), która uwzględnia imperfekcje oraz analizę strukturalną zgodnie z teorią drugiego rzędu. Wyniki również pokazują, że różnice między oboma podejściami rozważającymi efekt imperfekcji w Metodzie 2 (tj. 5.3.2(3) i 5.3.2(11)) są raczej małe dla prostokątnych ram ciągłych.
W tym momencie możemy odnieść się do 5.3.2 (6) EN 1993-1-1:2005 [1], które sugeruje, że lokalne imperfekcje wygięcia mogą być pominięte przy wykonywaniu globalnej analizy w celu określenia sił końcowych i momentów końcowych do użycia w sprawdzeniach elementów zgodnie z 6.3.
Tak więc, imperfekcje mogą być wprowadzane tylko w formie globalnej imperfekcji przechyłu w tym przykładzie numerycznym, a sprawdzenia stateczności równoważnych elementów zgodnie z 6.3 [1] mogą być wykonane. Uwzględniając analizę drugiego rzędu i rozważenie globalnego zachowania ramowego, ta weryfikacja powinna być oparta na długości wyboczeniowej równej długości elementu, jak przewiduje 5.2.2 (7) b EN 1993-1-1:2005 [1]. Na końcu wyniki są pokazane na Obrazie 14.