Анализ зависимых от времени прогибов железобетонных элементов по ACI 318 с учётом длительных воздействий (полнзий и усадки по ACI 435)

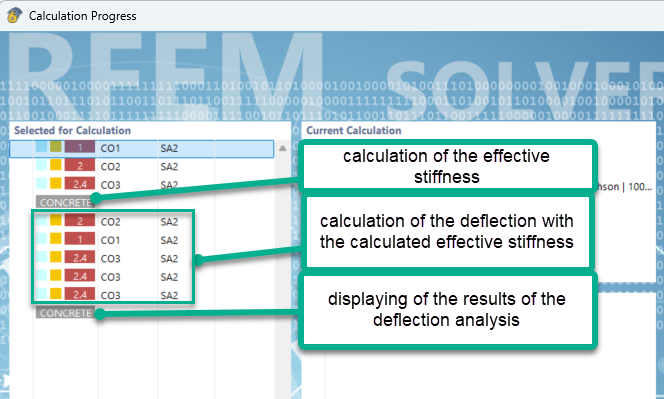
I. Исходные данные

1. Геометрия

Система: Балка на один пролёт Пролёт: l = 12 футов Ширина поперечного сечения: b = 93.0 дюймов Высота поперечного сечения: h = 6.0 дюймов Эффективная глубина: d = 6 – 0.650 – 0.3125 = 5.0375 дюймов

2. Материалы

• Бетон

Прочность на сжатие бетона: f’c = 3,000 ksi Модуль упругости: E = 3,122.019 ksi

Чтобы учесть ползучесть и усадку, необходимо активировать времязависимые свойства бетона:

Эти свойства теперь установлены для всех элементов и поверхностей с этим материалом. Однако возможно редактирование этих свойств для конкретного элемента, редактируя эти свойства в опциях поперечного сечения этого элемента:

• Армирующая сталь

Указанная прочность на текучесть: fy = 40,000 ksi Модуль упругости: Es = 29,000.0 ksi Количество арматуры: 11 стержней диаметром 0.625 дюймов Площадь арматуры: As,prov = 3.37 in² Коэффициент армирования: ρ = 0.60%

3. Конфигурация пригодности использования

Для учёта времязависимой деформации можно использовать два различных подхода:

• Времязависимый коэффициент согласно таблице 24.2.4.1.3
• Времязависимые свойства материала (ползучесть и усадка) согласно ACI 435

В этом примере используется второй подход; поэтому он выбран в конфигурации пригодности использования:

4. Нагрузки и комбинации нагрузок

Категории действий для случаев нагрузки определены в соответствии с ASCE 7.

• Случай нагрузки 1 (LC1)

Категория действия: Постоянная нагрузка (D) Случай нагрузки 1 включает собственный вес элемента и дополнительную равномерно распределённую нагрузку на элемент величиной 0.8 kip/ft.

• Случай нагрузки 2 (LC2)

Категория действия: Временная нагрузка (L) Случай нагрузки 2 состоит из равномерно распределённой нагрузки на элемент величиной 1.6 kip/ft.

• Проектные ситуации

Для анализа прогиба создается проектная ситуация на основе раздела 2.4 (ASD) ASCE 7 с использованием не упрочённых комбинаций нагрузок. В данной проектной ситуации активирован мастер комбинаций нагрузок для автоматического создания комбинаций нагрузок.

• Комбинации нагрузок

Создаются две комбинации нагрузок:

• CO1: LC1
• CO2: LC1 + LC2

В анализе прогиба ползучесть и усадка в железобетоне вызваны только длительными постоянными нагрузками, такими как собственный вес конструкции. Кратковременные нагрузки, такие как временные нагрузки, обычно не вносят значительного вклада в эти времязависимые эффекты. Чтобы точно зафиксировать ползучесть и усадку, необходимо определять длительные постоянные нагрузки в анализе. Затем рассчитываются прогибы, возникающие в результате этих постоянных нагрузок, и включаются в общий прогиб при оценке соответствующих комбинаций нагрузок. Это гарантирует, что долгосрочное поведение конструкции правильно учтено в оценке пригодности использования. Чтобы учесть эти эффекты в расчёте надстройки бетона, должна быть создана отдельная проектная ситуация. Эта проектная ситуация основана на разделе 2.4 (ASD) ASCE 7. Комбинационный мастер не назначен, так как комбинация нагрузок будет создана вручную, что позволяет точно контролировать, какие длительные постоянные нагрузки способствуют ползучести и усадке.

Чтобы указать надстройке бетонного проектирования, какая проектная ситуация включает комбинацию длительных постоянных нагрузок, тип предельного состояния проектной ситуации установлен в "Serviceability Design | Long-Term Sustained". Затем создается комбинация нагрузок с новой проектной ситуацией (DS2). В этом примере предполагается, что только собственный вес действует как длительная постоянная нагрузка, способствующая ползучести и усадке. Поэтому для точного зафиксирования времязависимых эффектов определена комбинация нагрузок, включающая только собственный вес (LC1). Созданная комбинация нагрузок CO3 затем используется для расчёта долгосрочного прогиба элемента из-за постоянной нагрузки. Чтобы включить этот прогиб при оценке общего прогиба, CO3 назначается в качестве соответствующей комбинации нагрузок (CO) для двух комбинаций нагрузок DS2. С назначенной соответствующей нагрузкой в конфигурации пригодности использования обнаружение состояния трещин установлено как "Crack state from corresponding CO of SLS design situation from associated load". Это обеспечивает расчет коэффициента распределения ζd как максимального значения для всех соответствующих нагрузок.

II. Расчёт проектирования бетона

Для анализа деформаций в надстройке проектирования бетона используется аналитический метод для 2D конструкций и 1D элементов, которые подвергаются воздействию продольных сил и изгибающих моментов. Это основано на определении эффективных жесткостей (метод эффективной жесткости) на плоскости поперечного сечения, с учётом состояния трещин, а также таких эффектов, как натяжение и простые долговременные эффекты.

1. Расчёт прогиба из-за длительной постоянной нагрузки

a. Кривизна для состояния без трещин

В этом разделе представлен расчет долгосрочного прогиба элемента под CO3 (собственный вес, включая эффекты ползучести и усадки). Проверка проектирования проводится в критической точке x = 6.0 футов, где присутствует только изгибающий момент M_y,u = 14.40 kipft. Продольная сила в этой точке P_u = 0.

Эффекты ползучести учитываются за счет уменьшения модуля упругости. Влияние ползучести учтено с использованием предельного коэффициента ползучести 𝜑: Эффективный модуль упругости бетона: \(\mathrm{E_{c,eff}} = \dfrac{\mathrm{E_{c}}}{1 + \phi}\) \(\mathrm{E_{c,eff}} = \dfrac{3122.020\,\mathrm{ksi}}{1 + 3.200} = 743.319\,\mathrm{ksi}\)

Эффективное модульное соотношение: \(\alpha_{e} = \dfrac{E_{s}}{E_{c,eff}}\) \(\alpha_{e} = \dfrac{29000.000\,\mathrm{ksi}}{743.319\,\mathrm{ksi}} = 39.01\)

Эффективное модульное соотношение (кратковременная нагрузка): \(\alpha_{e,st} = \dfrac{E_{s}}{E_{c}}\) \(\alpha_{e,st} = \dfrac{29000.000\,\mathrm{ksi}}{3122.020\,\mathrm{ksi}} = 9.29\)

Эффективные модульные соотношения используются для расчета геометрических параметров для состояния без трещин (кратковременного и долговременного) и в состоянии трещин:

Состояние I - Состояние без трещин
Описание	Символ	Значение	Единица измерения
Расстояние от центра тяжести идеального сечения от поверхности бетона в сжатии (определено для состояния без трещин)	zI	3.389	дюймов
Эффективная площадь сечения в состоянии без трещин	AI	689.664	дюймов2
Эффективный момент инерции к идеальному центру тяжести в состоянии без трещин	Iy,I	2116.230	дюймов4
Эксцентриситет идеального центра тяжести сечения в состоянии без трещин	ez,I	0.389	дюймов

Состояние I - Состояние без трещин - Кратковременная нагрузка
Описание	Символ	Значение	Единица измерения
Расстояние от центра тяжести идеального сечения от поверхности бетона в сжатии (определено для состояния без трещин)	zI,st	3.108	дюймов
Эффективная площадь сечения в состоянии без трещин	AI,st	589.348	дюймов2
Эффективный момент инерции к идеальному центру тяжести в состоянии без трещин	Iy,I,st	1797.210	дюймов4

Усадка: Усадка вызывает дополнительную продольную силу в арматуре. Из-за эксцентриситета армирования к центру тяжести идеального сечения, присутствует дополнительная кривизна, вызванная усадкой.

Затем рассчитывается дополнительная сила из-за усадки: \( \mathrm{P_{sh}} = - \mathrm{E_{s}} \cdot \varepsilon_{\mathrm{sh}} \cdot \left( \mathrm{A_{s,def,+z (bottom)}} + \mathrm{A_{s,def,-z (top)}} \right) \)

\( \mathrm{P_{sh}} = -29000.000\,\mathrm{ksi} \cdot -0.600000\,\text{‰} \cdot \left( 3.37\,\mathrm{in^2} + 0.00\,\mathrm{in^2} \right) = 58.721\,\mathrm{kip} \)

Эксцентриситет силы усадки к центру тяжести идеального сечения в состоянии без трещин затем равен:

\(\mathrm{e_{sh,z,I}} = \dfrac{A_{s,def,+z (bottom)} \cdot d_{def,+z (bottom)} + A_{s,def,-z (top)} \cdot d_{def,-z (top)}}{A_{s,def,+z (bottom)} + A_{s,def,-z (top)}} - \mathrm{z_{I}}\)

\(\mathrm{e_{sh,z,I}} = \dfrac{3.37\,\mathrm{in^2} \cdot 5.037\,\mathrm{in} + 0.00\,\mathrm{in^2} \cdot 3.000\,\mathrm{in}}{3.37\,\mathrm{in^2} + 0.00\,\mathrm{in^2}} - 3.389\,\mathrm{in} = 1.649\,\mathrm{in}\)

В результате возникает изгибающий момент, вызванный продольной силой P_sh: \(\mathrm{M_{sh,y,I}} = \mathrm{P_{sh}} \cdot \mathrm{e_{sh,z,I}}\)

\(\mathrm{M_{sh,y,I}} = 58.721\,\mathrm{kip} \cdot 1.649\,\mathrm{in} = 8.07\,\mathrm{kipft}\)

Затем определяется коэффициент кривизны для состояния без трещин. Он указывает, как момент усадки действует по отношению к осевой силе и её эксцентриситету. Он показывает, как распределение усадочных сил и расположение центра масс влияют на деформации элемента. Это значение имеет решающее значение для полного описания деформаций поперечного сечения из-за усадки: \(\mathrm{k_{sh,y,I}} = \dfrac{\mathrm{M_{sh,y,I}} + \mathrm{M_{y,Ed,def}} - \mathrm{P_{u}} \cdot \mathrm{e_{z,I}}}{\mathrm{M_{y,Ed,def}} - \mathrm{P_{u}} \cdot \mathrm{e_{z,I}}}\)

\(\mathrm{k_{sh,y,I}} = \dfrac{8.07\,\mathrm{kipft} + 14.40\,\mathrm{kipft} - 0.000\,\mathrm{kip} \cdot 0.389\,\mathrm{in}}{14.40\,\mathrm{kipft} - 0.000\,\mathrm{kip} \cdot 0.389\,\mathrm{in}} = 1.560\)

Теперь можно рассчитать общую кривизну для состояния без трещин:

\(\kappa_{y,I} = \mathrm{k_{sh,y,I}} \cdot \dfrac{\mathrm{M_{y,Ed,def}} - \mathrm{P_{u}} \cdot \mathrm{e_{z,I}}}{E_{c,eff} \cdot \mathrm{I_{y,I}}}\) \(\kappa_{y,I} = 1.560 \cdot \dfrac{14.40\,\mathrm{kipft} - 0.000\,\mathrm{kip} \cdot 0.389\,\mathrm{in}}{743.319\,\mathrm{ksi} \cdot 2116.230\,\mathrm{in^4}} = 2.1\,\mathrm{mrad/ft}\)

b. Кривизна для состояния трещин

Состояние II - Состояние трещин -
Описание	Символ	Значение	Единица измерения
Глубина зоны сжатия в состоянии трещин	cII	2.618	дюймов
Расстояние от центра тяжести идеального сечения от поверхности бетона в сжатии (определено для состояния трещин)	zII	2.618	дюймов2
Эффективная площадь сечения в состоянии трещин	AII	375.100	дюймов2
Эффективный момент инерции к идеальному центру тяжести в состоянии трещин	Iy,II	1326.990	дюймов4
Эксцентриситет идеального центра тяжести сечения в состоянии трещин	ez,II	-0.382	дюймов

Усадка - Состояние трещин
Описание	Символ	Значение	Единица измерения
Эксцентриситет силы усадки к центру тяжести идеального сечения в состоянии трещин	esh,z,II	2.420	дюймов
Изгибающий момент, вызванный продольной силой Nsh для состояния трещин	Msh,y,II	11.84	kipft
Коэффициент кривизны для состояния трещин	ksh,y,II	1.822	-

\(\kappa_{y,II} = \mathrm{k_{sh,y,II}} \cdot \dfrac{\mathrm{M_{y,Ed,def}} - \mathrm{P_{u}} \cdot \mathrm{e_{z,II}}}{E_{c,eff} \cdot \mathrm{I_{y,II}}}\) \(\kappa_{y,II} = 1.822 \cdot \dfrac{14.40\,\mathrm{kipft} - 0.000\,\mathrm{kip} \cdot (-0.382\,\mathrm{in})}{743.319\,\mathrm{ksi} \cdot 1326.990\,\mathrm{in^4}} = 3.8\,\mathrm{mrad/ft}\)

c. Кривизна для состояний без трещин и трещин

Максимальное напряжение в состоянии без трещин при кратковременной и долговременной нагрузке рассчитывается и затем сравнивается. Большее из двух значений используется для определения коэффициента распределения.

Максимальное напряжение в состоянии без трещин
Описание	Символ	Значение	Единица измерения
Максимальное напряжение в состоянии без трещин (долговременная нагрузка)	fmax,lt	0.418	ksi
Максимальное напряжение в состоянии без трещин (кратковременная нагрузка)	fmax,st	0.278	ksi

Коэффициент распределения рассчитывается по следующей формуле: \(\zeta_{d} = 1 - \left( \dfrac{\dfrac{2}{3} \cdot f_{r}}{f_{max}} \right)^2\) \(\zeta_{d} = 1 - \left( \dfrac{\dfrac{2}{3} \cdot 0.411\,\mathrm{ksi}}{0.418\,\mathrm{ksi}} \right)^2 = 0.570\)

\(\kappa_{y,f} = \zeta_{d} \cdot \kappa_{y,II} + (1 - \zeta_{d}) \cdot \kappa_{y,I}\) \(\kappa_{y,f} = 0.570 \cdot 3.8\,\mathrm{mrad/ft} + (1 - 0.570) \cdot 2.1\,\mathrm{mrad/ft} = 3.1\,\mathrm{mrad/ft}\)

d. Финальная жесткость

Используя полученный коэффициент распределения вместе с параметрами поперечного сечения в состояниях с трещинами и без трещин, теперь можно определить эффективные параметры поперечного сечения:

Эффективные параметры поперечного сечения
Описание	Символ	Значение	Единица измерения
Площадь идеального сечения	Af	466.537	дюймов2
Идеальный момент инерции к идеальному центру сечения	Iy,f	909.112	дюймов4
Эксцентриситет центра тяжести	ez,f	-0.135	дюймов
Идеальный момент инерции к геометрическому центру сечения	Iy,0,f	917.601	дюймов4

Поскольку в данном примере единственной внутренней силой является изгибающий момент, только касательная жесткость на изгиб является значимой:

\(\mathrm{EI_{y,0,f}} = E_{c,eff} \cdot \mathrm{I_{y,0,f}}\) \(\mathrm{EI_{y,0,f}} = 743.319\,\mathrm{ksi} \cdot 917.601\,\mathrm{in^4} = 4736.60\,\mathrm{kipft^2}\)

С помощью вновь рассчитанной эффективной жесткости затем проводится новый статический анализ для получения прогиба:

Получено вертикальное отклонение в 0.420 дюймов на середине пролёта балки.

Предельный прогиб определяется как: \(\mathrm{u_{z,lim}} = \dfrac{L_{z,ref}}{L_{z,ref} / u_{z,lim}}\)

\(\mathrm{u_{z,lim}} = \dfrac{12.00\,\mathrm{ft}}{240.000} = 0.600\,\mathrm{in}\)

На основе этого коэффициент проверки проектирования рассчитывается как: \(\eta = \left|\dfrac{u_{z}}{u_{z,lim}}\right|\)

\(\eta = \left|\dfrac{0.420\,\mathrm{in}}{0.600\,\mathrm{in}}\right| = 0.701\)

2. Расчет полной нагрузки на прогиб

Для полного прогиба управляющей является комбинация нагрузок CO2 (LC1 + LC2). Присутствует изгибающий момент в 43.20 kipft. Поскольку только постоянные нагрузки вызывают ползучесть и усадку, эффекты ползучести не учитываются при расчетах свойств поперечного сечения для кратковременных нагрузок. Поэтому для расчета используется эффективный модуль упругости бетона E_c, и коэффициент кривизны для усадки устанавливается равным 1.0.

a. Кривизна для состояния без трещин

Геометрические параметры в состоянии без трещин соответствуют кратковременным геометрическим параметрам постоянной нагрузки:

Состояние I - Состояние без трещин
Описание	Символ	Значение	Единица измерения
Расстояние от центра тяжести идеального сечения от поверхности бетона в сжатии (определено для состояния без трещин)	zI	3.108	дюймов
Эффективная площадь сечения в состоянии без трещин	AI	589.348	дюймов2
Эффективный момент инерции к идеальному центру тяжести в состоянии без трещин	Iy,I	1797.210	дюймов4
Эксцентриситет идеального центра тяжести сечения в состоянии без трещин	ez,I	0.108	дюймов

Кривизна в состоянии без трещин затем рассчитывается: \(\kappa_{y,I} = k_{sh,y,I} \cdot \frac{M_{y,Ed,def} - P_{u} \cdot e_{z,I}}{E_{c,eff} \cdot I_{y,I}} \)

\(\kappa_{y,I} = 1.000 \cdot \frac{43.20\,\text{kipft} - 0.000\,\text{kip} \cdot 0.108\,\text{in}}{3122.020\,\text{ksi} \cdot 1797.210\,\text{in}^4} = 1.1\,\text{mrad/ft}\)

b. Кривизна для состояния трещин

Геометрические параметры в состоянии трещин для кратковременных нагрузок определяются без учёта эффектов ползучести:

Состояние II - состояние трещин
Описание	Символ	Значение	Единица измерения
Глубина зоны сжатия в состоянии трещин	cII	1.536	дюймов
Расстояние от центра тяжести идеального сечения от поверхности бетона в сжатии (определено для состояния трещин)	zII	1.536	дюймов
Эффективная площадь сечения в состоянии трещин	AII	174.226	дюймов2
Эффективный момент инерции к идеальному центру тяжести в состоянии трещин	Iy,II	496.674	дюймов4

Кривизна в состоянии трещин затем рассчитывается: \(\kappa_{y,II} = k_{sh,y,II} \cdot \frac{M_{y,Ed,def} - P_{u} \cdot e_{z,II}}{E_{c,eff} \cdot I_{y,II}}\)

\(\kappa_{y,II} = 1.000 \cdot \frac{43.20\,\text{kipft} - 0.000\,\text{kip} \cdot (-1.464)\,\text{in}}{3122.020\,\text{ksi} \cdot 496.674\,\text{in}^4} = 4.0\,\text{mrad/ft}\)

c. Кривизна из состояний без трещин и трещин

Для расчета коэффициента распределения требуется максимальное напряжение в состоянии без трещин для этого поперечного сечения: \(f_{max} = \frac{P_{u}}{A_{I}} + \frac{M_{y,Ed,def} - P_{u} \cdot \left( z_{I} - \frac{h}{2} \right)}{I_{y,I}} \cdot \left( h - z_{I} \right)\)

Полученный коэффициент распределения затем: \(f_{max} = \frac{0.000\,\text{kip}}{589.348\,\text{in}^2} + \frac{43.20\,\text{kipft} - 0.000\,\text{kip} \cdot \left( 3.108\,\text{in} - \frac{6.000\,\text{in}}{2} \right)}{1797.210\,\text{in}^4} \cdot \left( 6.000\,\text{in} - 3.108\,\text{in} \right) = 0.834\,\text{ksi}\)

Наконец, окончательная кривизна рассчитывается: \(\kappa_{y,f} = \zeta_{d} \cdot \kappa_{y,II} + \left( 1 - \zeta_{d} \right) \cdot \kappa_{y,I}\)

\(\kappa_{y,f} = 0.892 \cdot 4.0\,\text{mrad/ft} + \left( 1 - 0.892 \right) \cdot 1.1\,\text{mrad/ft} = 3.7\,\text{mrad/ft}\)

d. Финальная жесткость

Теперь можно определить эффективные параметры поперечного сечения:

Эффективные параметры поперечного сечения
Описание	Символ	Значение	Единица измерения
Площадь идеального сечения	Af	188.543	дюймов2
Идеальный момент инерции к идеальному центру сечения	Iy,f	538.700	дюймов4
Эксцентриситет центра тяжести	ez,f	-1.413	дюймов
Идеальный момент инерции к геометрическому центру сечения	Iy,0,f	915.074	дюймов4

Жесткость на изгиб теперь можно рассчитать: \(EI_{y,0,f} = E_{c,eff} \cdot I_{y,0,f}\)

\(EI_{y,0,f} = 3122.020\,\text{ksi} \cdot 915.074\,\text{in}^4 = 19839.40\,\text{kipft}^2\)

Используя рассчитанную эффективную жесткость, рассчитывается кратковременный полный прогиб. Достигнуто отклонение в 0.984.

Расчет полного прогиба балки при частых нагрузках требует учета различных компонентов деформации, возникающих от различных типов нагрузок и их соответствующих эффектов на элемент. Долгосрочные и кратковременные деформации должны рассматриваться отдельно, чтобы правильно определить фактический прогиб:

\(u_{z,tot} = u_{z,QP,lt} + \left( u_{z,tot,st} - u_{z,QP,st} \right)\)

• u_z,QP,lt: Этот прогиб вызван длительными постоянными нагрузками и учитывает эффекты ползучести, которые элемент будет испытывать в течение длительного времени. Это отклонение, рассчитанное в разделе 1.

• u_z,tot,st: Кратковременный полный прогиб. Эта деформация происходит сразу после приложения частой нагрузки. Это прогиб, рассчитанный в этом разделе.

• u_z,QP,st: Кратковременный полный прогиб длительных постоянных нагрузок. Эта деформация развивается непосредственно после приложения постоянных нагрузок и представляет собой мгновенный отклик элемента до того, как начнутся эффекты ползучести.

Общий прогиб u_z,tot состоит из долгосрочного прогиба u_z,QP,lt из-за длительных постоянных нагрузок и дополнительного прогиба от кратковременных эффектов. Этот дополнительный прогиб рассчитывается как разница между общим кратковременным прогибом u_z,tot,st и кратковременным прогибом, вызванным нагрузками, вызывающими ползучесть u_z,QP,st. Следующая графика ясно это иллюстрирует:

\(u_{z,tot} = u_{z,QP,lt} + \left( u_{z,tot,st} - u_{z,QP,st} \right)\)

\(u_{z,tot} = 0.420\,\text{in} + \left( 0.630\,\text{in} - 0.067\,\text{in} \right) = 0.984\,\text{in}\)

\(\eta = \left|\dfrac{0.984\,\mathrm{in}}{0.600\,\mathrm{in}}\right| = 1.640 >1 \) В этом случае общий прогиб превышает предел, и проверка проектирования не выполнена.

В заключение, этот пример демонстрирует всесторонний расчет прогибов железобетонной балки с учетом как кратковременных, так и долгосрочных эффектов, включая ползучесть и усадку. Используя надстройку RFEM Concrete Design, эффективная жесткость балки была определена с помощью аналитического метода, учитывающего состояния с трещинами и без трещин, натяжение и времязависимые свойства материала. Сначала был рассчитан долгосрочный прогиб под действием постоянных нагрузок (0.420 дюйма), затем полный кратковременный прогиб под частыми нагрузками (0.984 дюйма). В совокупности общий прогиб (0.984 дюйма) превышает допустимый предел (0.600 дюйма), что приводит к коэффициенту проверки проектирования 1.64, указывающему на то, что балка не отвечает требованиям пригодности к эксплуатации. Это подчеркивает критическую важность точного моделирования времязависимого поведения бетона и комбинаций нагрузок в анализе пригодности к эксплуатации.