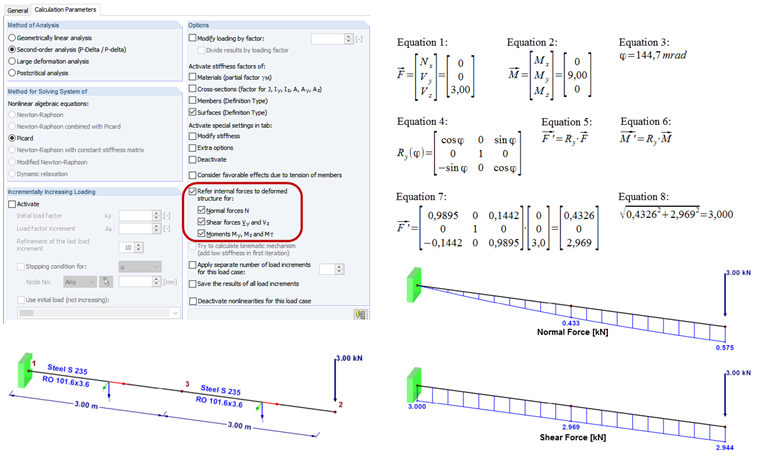
В параметрах расчета программ RFEM и RSTAB для каждого сочетания нагрузок и каждого загружения доступна опция «Отнести внутренние силы к деформированной конструкции». Это требует расчета по методу второго порядка.
Важность этого поясняется на простом примере консоли, на которую действует нагрузка (см. рисунок).
Нагрузка консоли вызывает небольшой поворот в Узле 3. При расчете по теории второго порядка, используйте эту опцию, чтобы решить, относятся ли внутренние силы в данном узле к исходной или повернутой системе координат. При расчете конструктивной системы по геометрически линейному методу мы получим следующие внутренние силы (RO 101.6x3.6, S235):
Nх = 0
Vy = 0
Vz = 3,00 кН
Mикс = 0
My = 9,00 кНм
Mz = 0
Силы и моменты в любом случае можно рассматривать в виде вектора (формула 1 и формула 2). В узле 3 возникает вращение по формуле 3.
Таким образом, местная система координат стержня в данном месте будет повернута на уголφy. Теперь нужно преобразовать внутренние силы во повернутую систему координат. Это выполняется путем умножения вектора на матрицу поворота (см. ссылку в конце данного вопроса). Матрица для поворота вокруг оси y показана в формуле 4. Для преобразования используются Формула 5 и Формула 6. При вставке чисел мы получим формулу 7.
Получается, что небольшая часть поперечной силы становится растягивающей силой:
Nx = 0,4326 кН
Vy = 0
Vz = 2,969 кН
Вектор момента остается неизменным.
В этом простом случае мы можем проверить расчет по формуле 8.
Это в принципе и объясняет данный вариант расчета. Но что такое «правильные» внутренние силы? В любом случае внутренние силы, относящиеся к повернутой системе координат, являются более точными. Однако расчёт по теории второго порядка требует небольших поворотов. Таким образом, результаты не должны существенно отличаться. Если да, то необходимо выполнить расчет по методу больших деформаций. В этом случае допускаются большие повороты, а результаты всегда относятся к повернутой системе координат. В расчетах по геометрически линейному методу внутренние силы всегда относятся к исходной системе координат.