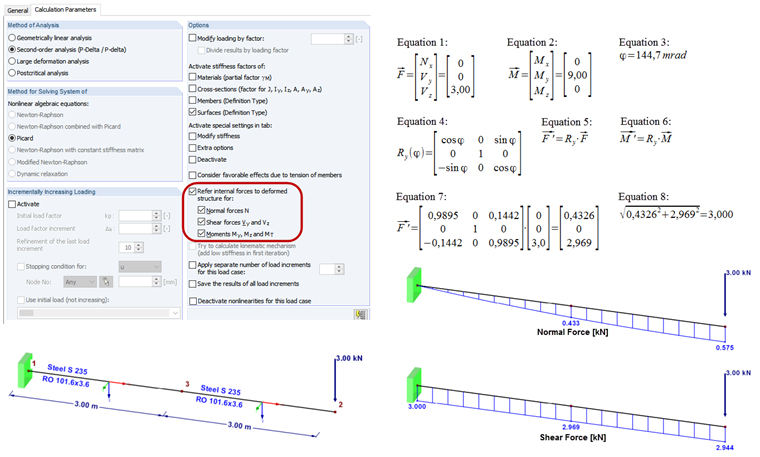
Nos parâmetros de cálculo do RFEM e do RSTAB, está disponível a opção "Referir esforços internos à estrutura deformada" para cada combinação de carga e caso de carga. Isto requer o cálculo de acordo com a análise de segunda ordem.
A importância disso é explicada com base num exemplo simples de uma viga em consola sujeita a uma carga (ver Figura).
O carregamento da consola causa uma pequena rotação no nó 3. Quando calcula de acordo com a análise de segunda ordem, utilize esta opção para decidir se as forças internas neste nó estão relacionadas com o sistema de coordenadas original ou rodado. Ao calcular o sistema estrutural de acordo com a análise geometricamente linear, são obtidos os seguintes esforços internos (RO 101.6×3.6, S235):
Nx= 0
Vy = 0
Vz = 3,00 kN
Mx= 0
My = 9,00kNm
M-z = 0
As forças e os momentos podem ser considerados como um vetor (fórmula 1 e 2) em cada caso. No nó 3, ocorre uma rotação de acordo com a Fórmula 3.
Assim, o sistema de eixos local da barra é rodado nesta posição de um ângulo φy. Agora, é necessário converter as forças internas para o sistema de coordenadas rodado. Isto é realizado através da multiplicação do vetor pela matriz de rotação (ver ligação no final desta FAQ). A matriz de rotação para a rotação sobre o eixo y é apresentada na Fórmula 4. Para a conversão, são utilizadas a Fórmula 5 e a Fórmula 6. Ao inserir os números, obtém-se a Fórmula 7.
Verifica-se que uma pequena parte da força de corte torna-se uma força de tração:
Nx =0,4326 kN
Vy = 0
Vz = 2,969 kN
O vetor de momento permanece inalterado.
Neste caso simples, pode verificar o cálculo como apresentado na Fórmula 8.
Isto explica o que faz esta opção de cálculo. Mas quais são os esforços internos "corretos"? Em qualquer caso, as forças internas relacionadas com o sistema de coordenadas rodado são mais precisas. No entanto, o cálculo de acordo com a teoria de segunda ordem requer pequenas rotações. Assim, os resultados não devem diferir significativamente. Se existirem, é necessário calcular de acordo com a análise das grandes deformações. Neste caso, são permitidas grandes rotações e os resultados estão sempre relacionados com o sistema de coordenadas rodado. Para os cálculos de acordo com a análise geométrica linear, os esforços internos estão sempre relacionados com o sistema de coordenadas original.