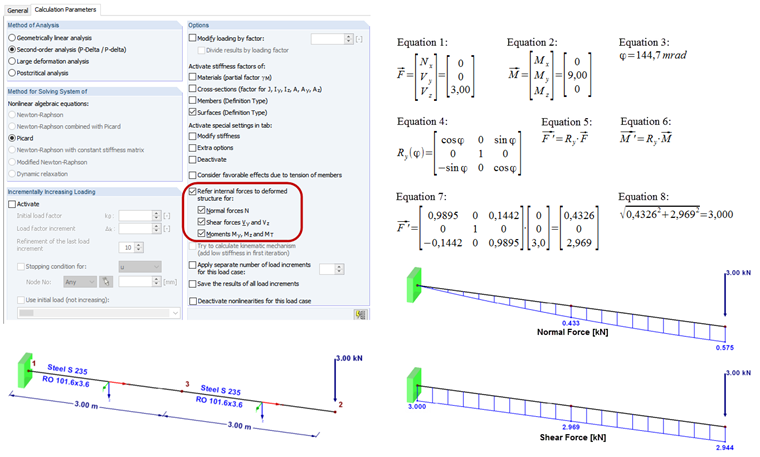
L’option « Référer les efforts internes à la structure déformée » est disponible pour chaque combinaison de charges et chaque cas de charge dans les paramètres de calcul de RFEM et RSTAB. Cela nécessite un calcul selon l’analyse du second ordre.
L’importance de cet aspect est expliquée à l’aide d’un exemple simple de porte-à-faux chargé (voir image).
La charge du porte-à-faux provoque une petite rotation au nœud 3. Lors du calcul selon l’analyse du second ordre, utilisez cette option pour décider si les efforts internes à ce nœud sont relatifs au système de coordonnées d’origine ou pivoté. Si le système est calculé selon l’analyse géométriquement linéaire, les efforts internes suivants sont obtenus (RO 101,6 x 3,6, S235) :
Nx = 0
Vy = 0
Vz = 3,00 kN
Mx = 0
My = 9,00 kNm
Mz = 0
Les efforts et les moments peuvent être considérés comme un vecteur (formule 1 et formule 2). Au nœud 3, il y a une rotation selon la formule 3.
Ainsi, le système d’axes de barre local est pivoté à cet emplacement selon l’angle φy. Il est maintenant nécessaire de convertir les efforts internes dans le système de coordonnées de rotation. Cette opération est effectuée en multipliant le vecteur par la matrice de rotation (voir le lien au bas de cet article). La matrice de rotation pour la rotation autour de l’axe y est affichée dans la formule 4. Les formules 5 et 6 sont utilisées pour la conversion. En insérant les nombres, on obtient la Formule 7.
Il s’avère qu’une petite partie de l’effort tranchant se transforme en effort de traction :
Nx = 0,4326 kN
Vy = 0
Vz = 2,969 kN
Le vecteur de moment reste inchangé.
Dans ce cas simple, vous pouvez vérifier le calcul comme indiqué dans la formule 8.
Ceci explique le rôle de cette option de calcul. Mais quels sont les efforts internes « corrects » ? Dans tous les cas, les efforts internes relatifs au système de coordonnées pivoté sont plus précis. Cependant, le calcul selon l’analyse du second ordre nécessite de faibles rotations. Les résultats ne doivent donc pas différer de manière significative. Si tel est le cas, le calcul doit être effectué selon l’analyse des grandes déformations. Dans ce cas, les grandes rotations sont autorisées et les résultats sont toujours rapportés au système de coordonnées pivoté. Pour les calculs selon l’analyse géométriquement linéaire, les efforts internes sont toujours rapportés au système de coordonnées d’origine.