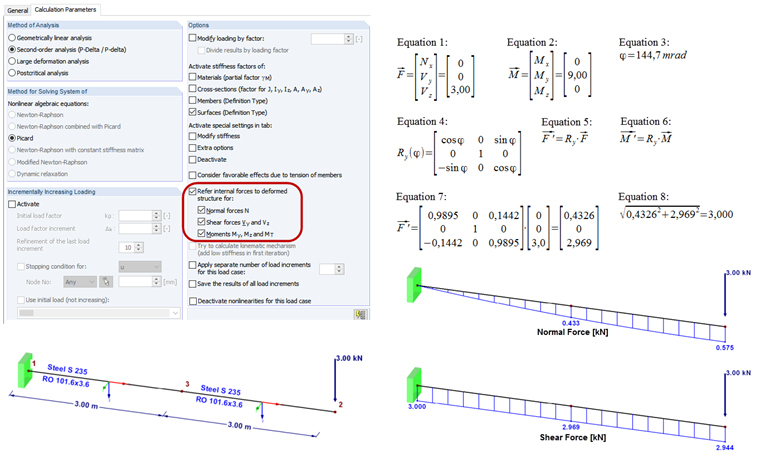
In Calculation Parameters of RFEM and RSTAB, the "Refer internal forces to deformed structure" option is available for each load combination and each load case. This requires the calculation according to the second-order analysis.
The importance of this is explained on a simple example of a cantilever subjected to a load (see the image).
The load of the cantilever causes a small rotation at Node 3. When calculating according to the second-order analysis, use this option to decide whether the internal forces at this node are related to the original or the rotated coordinate system. When calculating the structural system according to the geometrically linear analysis, the following internal forces are obtained (RO 101.6×3.6, S235):
Nx = 0
Vy = 0
Vz = 3.00 kN
Mx = 0
My = 9.00 kNm
Mz = 0
The forces and moments can be considered as a vector (Formula 1 and Formula 2) in each case. At Node 3, there is a rotation according to Formula 3.
Thus, the local member axis system is rotated at this location by the angle φy. Now, it is necessary to convert the internal forces to the rotated coordinate system. This is done by multiplying the vector by the rotation matrix (see the link below). The rotation matrix for the rotation about the y‑axis is shown in Formula 4. For the conversion, Formulas 5 and 6 are used. By inserting the numbers, Formula 7 is obtained.
It turns out that a small part of the shear force becomes a tension force:
Nx = 0.4326 kN
Vy = 0
Vz = 2.969 kN
The moment vector remains unchanged.
In this simple case, you can check the calculation as shown in Formula 8.
This explains what this calculation option does. But what are the "correct" internal forces? In any case, the internal forces related to the rotated coordinate system are more accurate. However, the calculation according to the second-order analysis requires small rotations. Thus, the results must not differ significantly. If they do, it is necessary to calculate according to the large deformation analysis. In this case, large rotations are allowed and the results are always related to the rotated coordinate system. For the calculations according to the geometrically linear analysis, the internal forces are always related to the original coordinate system.