Respuesta:
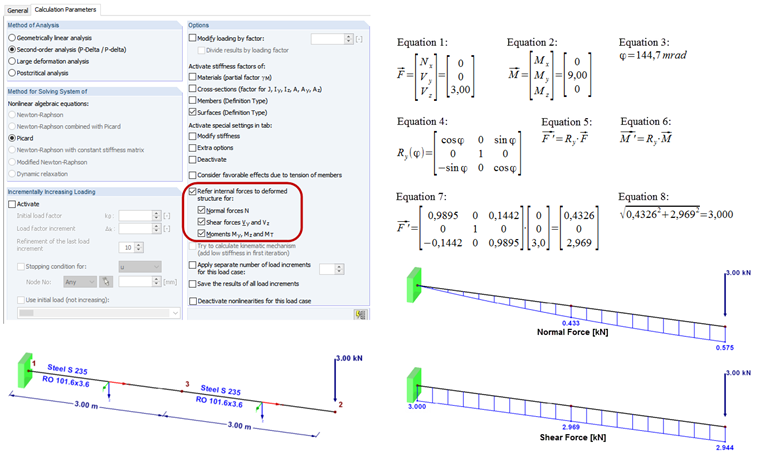
En los parámetros de cálculo de RFEM y RSTAB, hay una opción disponible de "Referir esfuerzos internos a la estructura deformada" para cada combinación de carga y cada caso de carga. Esto necesita el cálculo según el análisis de segundo orden. La importancia de esto se explica en un ejemplo simple de una viga de voladizo sujeta a una carga (ver figura).
La carga del voladizo causa un giro pequeño en el nudo 3. Al calcular según el análisis de segundo orden, utilice esta opción para decidir si los esfuerzos internos en este nudo están relacionados con el sistema de coordenadas original o girado. Si se calcula primero el sistema según el análisis geométricamente lineal, se obtienen los siguientes esfuerzos internos (RO 101-6x3.6, S235):
Nx = 0
Vy = 0
Vz = 3,00 kN
Mx = 0
My = 9,00 kNm
Mz = 0
Los esfuerzos y momentos se pueden considerar como un vector (fórmula 1 y 2) en cada caso. En el nudo 3, hay un giro según la fórmula 3.
Por lo tanto, el sistema de ejes local de la barra se gira en esta ubicación por el ángulo φy. Ahora, es necesario convertir los esfuerzos internos en el sistema de coordenadas girado. Esto se hace multiplicando el vector por la matriz de rotación (https://es.wikipedia.org/wiki/Matriz_de_rotación). La matriz de rotación para el eje de giro sobre el eje y se muestra en la fórmula 4. Para la conversión, se utilizan las fórmulas 5 y 6. Al insertar los números, se obtiene la fórmula 7.
Resulta que una pequeña parte del esfuerzo cortante se convierte en una fuerza de tracción:
Nx = 0,4326 kN
Vy = 0
Vz = 2,969 kN
El vector de momento permanece sin cambios.
En este caso simple, puede verificar el cálculo como se muestra en la fórmula 8.
Esto explica lo que hace esta opción de cálculo. Pero, ¿cuáles son los esfuerzos internos "correctos"? En cualquier caso, los esfuerzos internos relacionados con el sistema de coordenadas girado son más precisos. Sin embargo, el cálculo según el análisis de segundo orden necesita giros pequeños. Por lo tanto, los resultados no deben diferenciarse considerablemente. Si lo hacen, es necesario calcular según el análisis para grandes deformaciones. En este caso, se permiten los giros grandes y los resultados siempre se relacionan con el sistema de coordenadas girado. Para los cálculos según el análisis geométricamente lineal, los esfuerzos internos siempre están relacionados con el sistema de coordenadas original.
