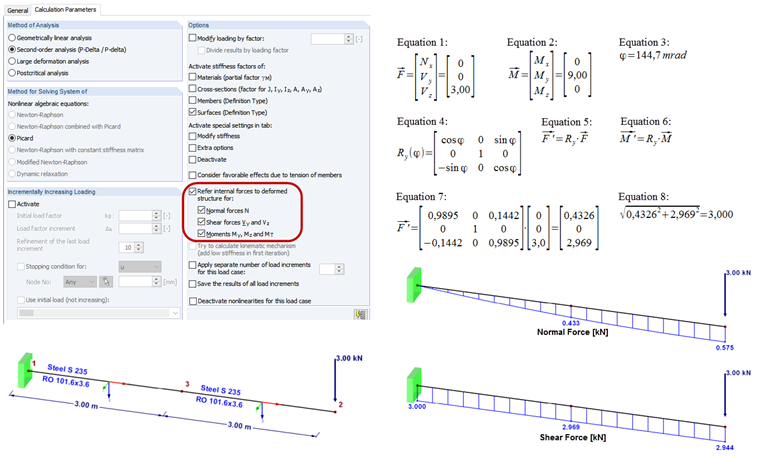
V parametrech výpočtu programů RFEM a RSTAB je pro každou kombinaci zatížení a pro každý zatěžovací stav možnost "Vztáhnout vnitřní síly na přetvořenou konstrukci". To vyžaduje výpočet podle teorie druhého řádu.
Význam tohoto je vysvětlen na jednoduchém příkladu zatížené konzoly (viz obrázek).
Zatížení konzoly způsobí malé pootočení v uzlu 3. Při výpočtu podle analýzy druhého řádu se můžeme rozhodnout, zda se vnitřní síly v tomto uzlu vztahují k původnímu nebo natočenému souřadnému systému. Pokud je systém poprvé vypočítán podle teorie prvního řádu, vzniknou následující vnitřní síly (RO 101,6×3,6, S235):
Nx = 0
Vy = 0
Vz = 3,00 kN
Mx = 0
My = 9,00 kNm
Mz = 0
Síly a momenty lze uvažovat jako vektor (vzorec 1 a vzorec 2). V uzlu 3 proběhne natočení podle vzorce 3.
Lokální osový systém prutu se tak v tomto místě natočí o úhel φy. Nyní by měly být vnitřní síly přepočítány na natočený souřadný systém. Toho dosáhneme vynásobením vektoru rotační maticí (viz odkaz pod touto FAQ). Rotační matice pro natočení okolo osy y je znázorněna ve vzorci 4. Pro přepočet se používají vzorce 5 a 6. Použitím čísel se získá vzorec 7.
Ukazuje se, že z malé části smykové síly se stane tahová síla:
Nx = 0,4326 kN
Vy = 0
Vz = 2,969 kN
Momentový vektor zůstává beze změny.
V tomto jednoduchém případě je možné zkontrolovat výpočet podle vzorce 8.
To vysvětluje, čeho lze dosáhnout zaškrtnutím volby v možnostech výpočtu. Jaké jsou ovšem "správné" vnitřní síly? Přesnější jsou v každém případě vnitřní síly, které se vztahují k natočenému souřadnému systému. Předpokladem pro výpočet podle teorie druhého řádu jsou ovšem malá natočení. Výsledky se tak nesmí výrazně lišit. Pokud tomu tak je, je nutné výpočet provést podle teorie třetího řádu. V takovém případě jsou přípustné i velká natočení a výsledky se vždy vztahují k natočenému souřadnému systému. U výpočtů podle teorie prvního řádu se vnitřní síly vztahují vždy k původnímu souřadnému systému.