Пользовательская история
В этом примере мы собираемся рассчитать средние значения силы для секции моста, такие как те, что применяются к конструктивным секциям в процессе проектирования на основе WTG-Merkblatt-M3.
Согласно рисунку 2.2 в WTG-Merkblatt-M3, данный пример классифицируется как Группа 1.
- G2: Абсолютные значения со средними требованиями к точности. Область применения может включать параметры или предварительные исследования, когда планируются последующие исследования с более высокой точностью (например, испытание в аэродинамической трубе класса G3).
- R2: Одиночные, все соответствующие направления ветра с достаточно мелким угловым разрешением.
- Z1: Статистические средние значения, при условии что они касаются стационарных процессов течения, где флуктуации (например, из-за турбулентности приближающегося потока) могут быть достаточно захвачены другими мерами.
- S1: Статические эффекты. Достаточно представить структурную модель с необходимой механической детальностью, но без массы и свойств демпфирования.
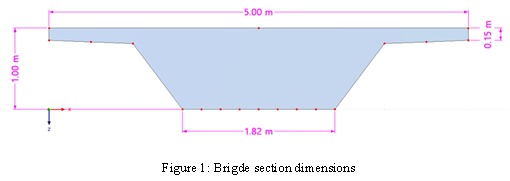
Размеры примера показаны на рисунке 1, а входная предпосылка иллюстрируется в таблице 1:
Таблица 1: Входные данные для примера проверки секции моста
| Модель | Секция моста |
|---|---|
| Основная скорость ветра | V = 30 м/с |
| Плотность воздуха | ρ = 1.225 кг/м³ |
| Решатель | На основе давления |
| Модель турбулентности | Постоянная k-ω SST |
| Тип профиля скорости ветра | Постоянный на высоте |
| Интенсивность турбулентности | 27% |
| Числовой алгоритм | Алгоритм SIMPLE |
| Дискретация | Второго порядка |
| Остаточное давление | 10⁻⁴ |
| Кинематическая вязкость | ν = 1.5 × 10⁻⁵ |
На рисунке 2 показано исследование плотности сетки в RWIND Pro для секции моста. Коэффициент силы 𝐶𝑓 незначительно уменьшается с 0.94 при плотности сетки 10% до 0.90 при плотности 25%, затем незначительно увеличивается до 0.92 при плотности 35%. Несмотря на небольшую флуктуацию, изменение остается в допустимой толерантности, указывая на то, что результаты достаточно стабильны для практического инжиниринга.
Также необходимо выполнить исследование вычислительной сетки в соответствии с приведенной ссылкой:
В этом примере мы сравним среднее значение силы ветра в x-направлении между EN 1991-1-4 и RWIND. Коэффициент силы cfx,o для секций моста можно получить, используя Рисунок 8.3 в EN 1991-1-4:
Сила в X-направлении - Упрощенный метод
Где было оценено, что процедуру динамического ответа не требуется, сила ветра в x-направлении может быть получена, используя выражение (8.2) в EN 1991-1-4:
vb=30 м/с является основной скоростью ветра C является фактором загрузки ветра. C=ce⋅cf,x=1.425×1.3=1.85 , где ce - это фактор воздействия, указанный в 4.5, а cf,x указан в 8.3.1(1) Aref,x=5 м2 - это референтная площадь, указанная в 8.3.1 ρ=1.225 кг/м3 является плотностью воздуха
WTG-Merkblatt M3 предоставляет два ключевых метода для проверки симуляционных результатов. Метод Коэффициент попадания оценивает, сколько из смоделированных значений Pi правильно соответствуют референсным значениям Oi в пределах заданной толерантности, используя бинарный классификационный подход (попадание или ошибка). Этот подход оценивает надежность симуляции, рассчитывая коэффициент попадания q, аналогичный функциям уверенности, использующимся в теории надежности. В отличие от этого, метод Нормализованная среднеквадратическая ошибка (e2) предоставляет более детальную оценку точности, количественно оценивая среднеквадратичное отклонение между смоделированными и референсными значениями, нормализованное для учета масштабных различий. Совместно эти методы предоставляют как качественные, так и количественные меры для проверки симуляции.
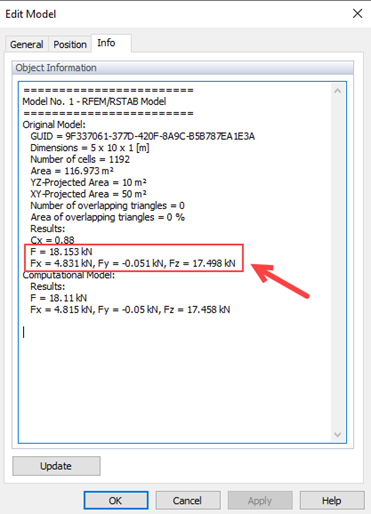
Результаты по Силе в RWIND и Сравнение с Еврокодом
В RWIND результаты по общим силам ветра доступны на вкладке Информация модели, как показано на рисунках 3 и 4. Разница между сценарием критического направления ветра RWIND (θ=0°) и Еврокодом составляет Wrel = 5.36% (ниже чем упомянутые критерии в WTG = 10%); тогда коэффициент попадания может быть получен как q=100%, что показывает хорошее согласование. Низкая нормализованная среднеквадратичная ошибка e2=0.002 также подтверждает сильное соответствие между симуляцией и измерениями, эффективно соответствуя стандартам проверки.