User Story
В этом примере мы будем рассчитывать локальные давления, средние давления и проводить параметрические исследования для предварительного проектирования с более точными методами, такими как трансзитный URANS.
Данный пример относится к группе 2, согласно рисунку 2.2 в WTG-Merkblatt-M3:
- G2: Абсолютные значения со средними требованиями к точности. Область применения может включать параметры или предварительные исследования, когда в дальнейшем планируются более точные исследования (например, испытание в аэродинамической трубе класса G3).
- R2: Солитарные, все релевантные направления ветра с достаточно тонким разрешением по направлениям.
- Z2: Среднестатистические значения и стандартные отклонения, при условии, что они касаются стационарных процессов течения, для которых достаточно статистического подтверждения флуктуаций с пиковым фактором.
- S1: Статические эффекты. Они достаточны для представления конструкции модели с необходимыми механическими деталями, но без свойств массы и демпфирования.
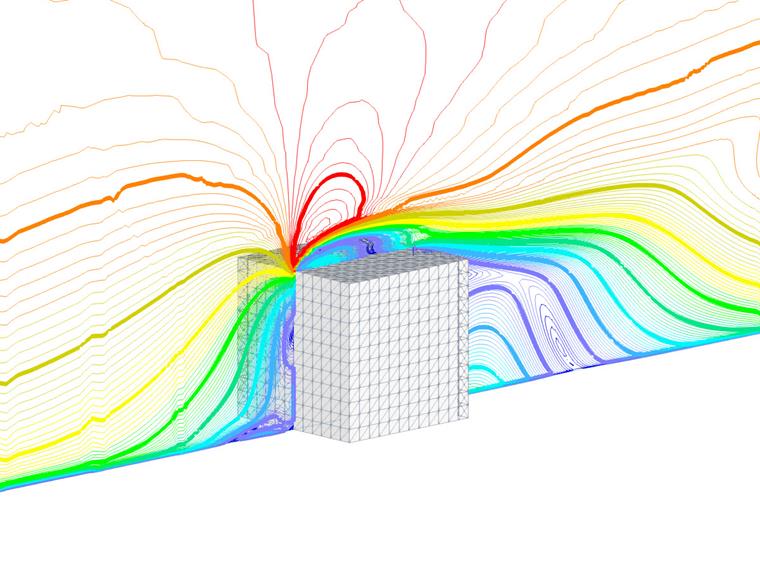
Размеры примера показаны на рисунке 1, а предположения входных данных представлены в таблице 1:
Table 1: Входные данные примера 3D куба
| Параметр | Символ | Значение | Единица |
|---|---|---|---|
| Базовая скорость ветра | V | 10.13 | м/с |
| Высота крыши | h | 6 | м |
| Горизонтальное измерение | α | 6 | м |
| Угол крыши | θкрыш | 0 | Градус |
| Плотность воздуха – RWIND | ρ | 1.25 | кг/м³ |
| Направления ветра | θветер | 0 | Градус |
| Модель турбулентности – RWIND | RANS & URANS | - | - |
| Кинематическая вязкость (Уравнение 7:15, EN 1991-1-4) – RWIND | ν | 1.5×10⁻⁵ | м²/с |
| Порядок схемы – RWIND | Первый и Второй | - | - |
| Целевое значение остатка – RWIND | 10⁻⁴ | - | - |
| Тип остатка – RWIND | Давление | - | - |
| Минимальное число итераций – RWIND | 800 | - | - |
| Пограничный слой – RWIND | NL | 10 | - |
| Тип функции стены – RWIND | Улучшенный / Смещенный | - | - |
Чувствительный анализ
В текущем примере чувствительный анализ показан на рисунке 2. Результаты суммарных сил сопротивления исследуются для четырех различных чисел сетки. Независимость от сетки достигается при 1.6 миллионах ячеек (Сетка #4).
WTG-Merkblatt M3 предоставляет два ключевых метода для валидации результатов моделирования. Метод Попаданий оценивает, сколько из смоделированных значений Pi правильно совпадают с эталонными значениями Oi в пределах определенной толерантности, используя бинарный подход классификации (попадание или промах). Этот подход оценивает надежность моделирования путем расчета коэффициента попаданий q, аналогичного функциям надежности, используемым в теории надежности. В отличие от этого, метод Нормализованной Среднеквадратической Ошибки (e2) предлагает более подробную оценку точности, масштабированно учитывая среднее квадратичное отклонение между смоделированными и эталонными значениями. Вместе эти методы предоставляют как качественные, так и количественные параметры для валидации моделирования.
Результаты
Диаграмма на рисунке 3 представляет распределение среднего и пикового коэффициента давления (Cp) вдоль заданной позиции на конструкции, сравнивая экспериментальные результаты с численными моделированиями, используя различные вычислительные модели. Экспериментальные данные включают измерения из полевого исследования Silsoe F-S и испытания в аэродинамической трубе (WT), в то время как моделирование осуществляется с использованием моделей RWIND RANS и RWIND URANS. Модель URANS дополнительно разделена на средние и пиковые значения для всестороннего анализа поведения аэродинамического давления.
Сравнение на рисунке 4 нацелено на оценку точности моделей моделирования RWIND в воспроизведении экспериментальных результатов. Ключевые статистические показатели, такие как коэффициент корреляции (R) и коэффициент детерминации (R²), представлены для количественной оценки согласования между моделируемыми и экспериментальными данными, предоставляющих представления о надежности этих моделей для аэродинамического анализа. Диагональная линия на референсном графике представляет идеальное совпадение между смоделированными и экспериментальными результатами, а близость данных к этой линии отражает точность каждой модели. Разница между RWIND и Еврокодом составляет Wотн,RANS = 11.54% и Wотн,URANS = 21.46%; тогда коэффициент попаданий может быть получен как qRANS=59% и qURANS,10%=30% и qURANS,20%=63%. Нормализованная среднеквадратическая ошибка рассчитана соответственно; e2RANS=0.02 и e2URANS=0.04.
Модель доступна для бесплатного скачивания здесь: