Histoire d’utilisateur
Dans cet exemple, nous allons calculer les valeurs moyennes des forces pour une section de pont, telles qu’applicables aux sections structurelles dans le processus de calcul basé sur WTG-Merkblatt-M3.
Selon la figure 2.2 de WTG-Merkblatt-M3, cet exemple est classé comme Groupe 1.
- G2 : valeurs absolues avec des exigences de précision moyenne. Le domaine d’application peut inclure des paramètres ou des études préliminaires lorsque des investigations ultérieures avec une plus grande précision sont prévues (par exemple, essai en soufflerie de classe G3).
- R2 : isolées, toutes les directions de vent pertinentes avec une résolution directionnelle suffisamment fine.
- Z1 : valeurs moyennes statistiques, à condition qu’elles concernent des processus de flux stationnaires où les fluctuations (par exemple, dues à la turbulence de l’écoulement approchant) peuvent être capturées suffisamment par d’autres mesures.
- S1 : effets statiques. Représenter le modèle structurel avec le détail mécanique requis, mais sans propriétés de masse et d’amortissement, suffit.
Les dimensions de l’exemple sont montrées dans la figure 1, et l’hypothèse d’entrée est illustrée dans le Tableau 1 :
Tableau 1 : Données d’entrée de l’exemple de vérification de la section du pont
| Modèle | Section de pont |
|---|---|
| Vitesse de base du vent | V = 30 m/s |
| Densité de l’air | ρ = 1,225 kg/m³ |
| Solveur | Basé sur la pression |
| Modèle de turbulence | k-ω SST stationnaire |
| Type de profil de vitesse du vent | Constant en hauteur |
| Intensité de la turbulence | 27 % |
| Algorithme numérique | Algorithme SIMPLE |
| Discrétisation | Second ordre |
| Pression résiduelle | 10⁻⁴ |
| Viscosité cinématique | ν = 1,5 × 10⁻⁵ |
La figure 2 montre une étude de sensibilité du maillage dans RWIND Pro pour une section de pont.
Le coefficient de force 𝐶𝑓 diminue légèrement de 0,94 à 10 % de densité de maillage à 0,90 à 25 % de densité, puis augmente marginalement à 0,92 à 35 % de densité.
Bien qu’il y ait une petite fluctuation, la variation reste dans une tolérance acceptable, indiquant une stabilité suffisante des résultats pour une utilisation pratique en ingénierie.
De plus, l’étude du maillage de calcul doit être effectuée comme le décrit l’article technique suivant :
Dans cet exemple, nous allons comparer la valeur moyenne de la force du vent en direction x entre l’EN 1991-1-4 et RWIND. Le coefficient de force cfx,o pour les sections de pont peut être obtenu en utilisant la figure 8.3 de l’EN 1991-1-4 :
Force en direction X - Méthode simplifiée
Une fois la procédure de réponse dynamique évaluée comme non requise, la force du vent en direction x peut être obtenue en utilisant l’expression (8.2) dans l’EN 1991-1-4 :
vb=30 m/s est la vitesse essentielle du vent
C est le facteur de charge du vent. C=ce⋅cf,x=1.425×1.3=1.85, où ce est le facteur d’exposition donné en 4.5 et cf,x est donné à 8.3.1(1)
Aref,x=5 m2 est la zone de référence donnée à 8.3.1
ρ=1,225 kg/m3 est la densité de l’air
WTG-Merkblatt M3 propose deux méthodes clés pour valider les résultats de simulation. La méthode du taux de réussite évalue combien des valeurs simulées Pi correspondent correctement aux valeurs de référence Oi dans une tolérance définie, en utilisant une approche de classification binaire (succès ou échec).
Cette approche évalue la fiabilité de la simulation en calculant un taux de réussite q, similaire aux fonctions de confiance utilisées dans la théorie de la fiabilité. En revanche, la méthode de l’erreur quadratique moyenne normalisée (e2) offre une évaluation plus détaillée de la précision en quantifiant l’écart quadratique moyen entre les valeurs simulées et les valeurs de référence, normalisée pour tenir compte des différences d’échelle. Ensemble, ces méthodes fournissent des mesures à la fois qualitatives et quantitatives pour la validation de la simulation.
Résultats de la force dans RWIND et comparaison avec l’Eurocode
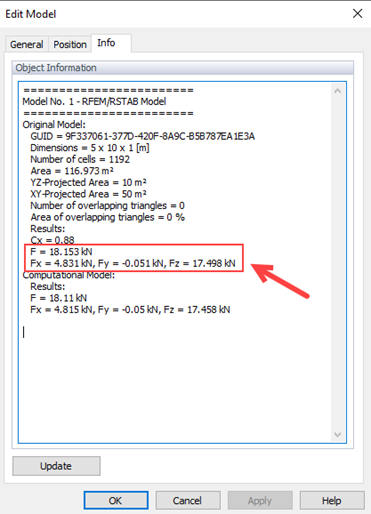
Dans RWIND, les résultats des forces totales du vent sont disponibles dans l’onglet Info de la boite de dialogue de modification du modèle comme le montrent les Figures 3 et 4. La différence entre le scénario de direction critique du vent RWIND (θ=0°) et l’Eurocode est d’environ Wrel = 5,36 % (inférieure au critère mentionné dans le WTG = 10 %). Le taux de réussite q=100% peut être obtenu, ce qui montre une bonne concordance. La faible erreur quadratique moyenne normalisée e2=0,002 confirme également une forte concordance entre la simulation et les mesures, répondant efficacement aux normes de validation.
.png)