=== User Story=== No exemplo, vamos calcular valores médios de força para uma seção de ponte, como aqueles aplicáveis a seções estruturais no processo de projeto com base no WTG-Merkblatt-M3
De acordo com a Figura 2.2 no WTG-Merkblatt-M3, este exemplo é classificado como Grupo 1.
- G2: Valores absolutos com requisitos de precisão média. A área de aplicação pode incluir parâmetros ou estudos preliminares quando investigações posteriores com maior precisão estão planejadas (por exemplo, exame de túnel de vento de classe G3).
- R2: Solitário, todas as direções de vento relevantes com resolução direcional suficientemente fina.
- Z1: Valores médios estatísticos, desde que se refiram a processos de fluxo estacionários onde flutuações (por exemplo, devido a turbulência de fluxo de aproximação) possam ser capturadas suficientemente por outras medidas.
- S1: Efeitos estáticos. É suficiente representar o modelo estrutural com o detalhe mecânico necessário, mas sem propriedades de massa e amortecimento.
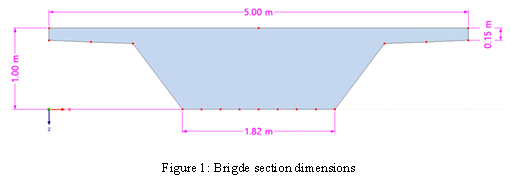
As dimensões do exemplo são mostradas na Figura 1, e a suposição de entrada é ilustrada na Tabela 1:
Tabela 1: Dados de Entrada do Exemplo de Verificação da Seção da Ponte
| Modelo | Seção da Ponte |
|---|---|
| Velocidade básica do vento | V = 30 m/s |
| Densidade do ar | ρ = 1.225 kg/m³ |
| Solver | Baseado em Pressão |
| Modelo de turbulência | Steady k-ω SST |
| Tipo de perfil de velocidade do vento | Constante em altura |
| Intensidade de Turbulência | 27% |
| Algoritmo numérico | Algoritmo SIMPLE |
| Discretização | Segunda Ordem |
| Pressão residual | 10⁻⁴ |
| Viscosidade cinemática | ν = 1.5 × 10⁻⁵ |
A Imagem 2 mostra um estudo de sensibilidade de malha no RWIND Pro para uma seção de ponte. O coeficiente de força 𝐶𝑓 diminui ligeiramente de 0.94 na densidade de malha de 10% para 0.90 na densidade de 25%, então aumenta marginalmente para 0.92 na densidade de 35%. Embora haja uma pequena flutuação, a variação permanece dentro de uma tolerância aceitável, indicando que os resultados são suficientemente estáveis para uso prático em engenharia.
Além disso, o estudo de malha computacional precisa ser realizado de acordo com o seguinte link:
Neste exemplo, iremos comparar o valor médio da força do vento na direção x entre EN 1991-1-4 e RWIND. O coeficiente de força cfx,o para seções de ponte pode ser obtido usando a Figura 8.3 em EN 1991-1-4:
Força na Direção X - Método Simplificado
Onde foi avaliado que um procedimento de resposta dinâmica não é necessário, a força do vento na direção x pode ser obtida usando a Expressão (8.2) em EN 1991-1-4:
vb=30 m/s é a velocidade essencial do vento C é o fator de carga do vento. C=ce⋅cf,x=1.425×1.3=1.85, onde ce é o fator de exposição dado em 4.5 e cf,x é dado em 8.3.1(1) Aref,x=5 m2 é a área de referência dada em 8.3.1 ρ=1.225 kg/m3 é a densidade do ar
O WTG-Merkblatt M3 fornece dois métodos principais para validar os resultados da simulação. O Método de Taxa de Acerto avalia quantos dos valores simulados Pi correspondem corretamente aos valores de referência Oi dentro de uma tolerância definida, usando uma abordagem de classificação binária (acerto ou erro). Essa abordagem avalia a confiabilidade da simulação calculando uma taxa de acerto q, semelhante a funções de confiança usadas na teoria de confiabilidade. Em contraste, o método Erro Quadrático Médio Normalizado (e2) oferece uma avaliação de precisão mais detalhada quantificando a média da diferença quadrada entre valores simulados e de referência, normalizada para considerar diferenças de escala. Juntos, esses métodos fornecem medidas qualitativas e quantitativas para validação de simulação.
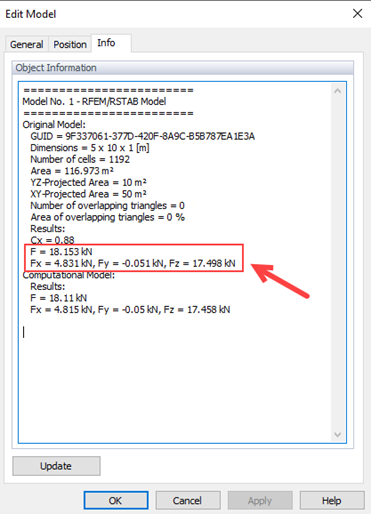
Resultados de Força no RWIND e Comparação com Eurocódigo
No RWIND, os resultados das forças totais do vento estão disponíveis na aba Info do modelo Editar, como mostrado nas Figuras 3 e 4. A diferença entre o cenário crítico de direção do vento do RWIND (θ=0°) e o Eurocódigo é de cerca de Wrel = 5.36% (inferior ao critério mencionado no WTG = 10%); então a taxa de acerto pode ser obtida como q=100%, o que mostra boa concordância. O baixo erro quadrático médio normalizado e2=0.002 também confirma forte concordância entre simulação e medições, atendendo efetivamente aos padrões de validação.