108x

2024-10-11

VE0064 | Толстостенный резервуар

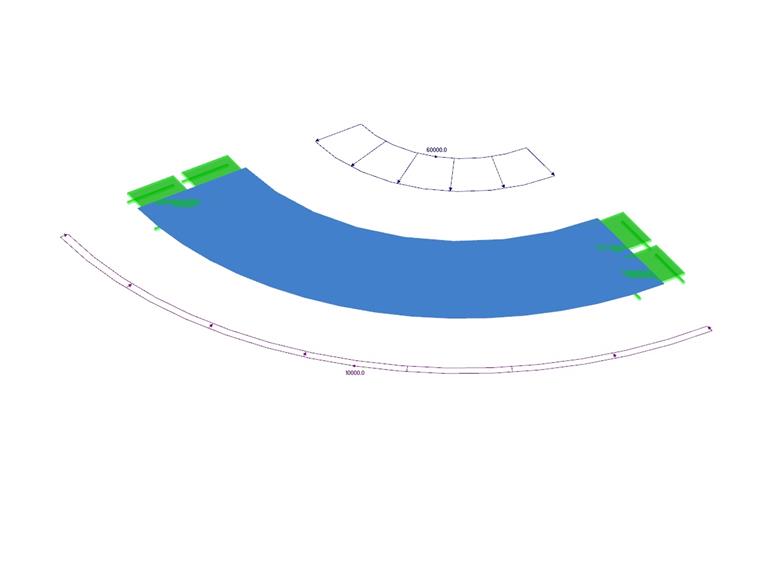
Описание работы

На толстостенный резервуар действует внутреннее и внешнее давление. Конструкция резервуара с открытыми концами, поэтому в нем возникает осевое напряжение. Проблема моделируется в виде четвертной модели. Определить радиальный прогиб внутреннего и внешнего радиуса u_r (r₁ ), u_r (r₂ ). Собственный вес не учитывается.

Материал	Упругое	Модуль упругости	E	1,000	МПа
Материал	Упругое	коэффициент Пуассона	ν	0,250	-
Геометрия		Внутренний радиус	r₁	200,000	мм
Геометрия		Внешний радиус	r₂	300.000	мм
Нагрузки		Внутреннее давление	p₁	60,000	кПа
Нагрузки		Внешнее давление	p₂	10,000	кПа

Толстостенный резервуар

Аналитическое решение

Напряженное состояние резервуара с толстыми стенками описывается уравнением равновесия

\frac{d σ_{r}}{d r} + \frac{σ_{r} - σ_{t}}{r} = 0

σ_r	Radial stress
σ_t	Tangential stress

Уравнение равновесия для массивного резервуара

С помощью уравнений деформации-прогиба и закона Гука мы получим дифференциальное уравнение второго порядка

\frac{d^{2} u_{r} (r)}{d r^{2}} + \frac{d u_{r} (r)}{d r} - \frac{u_{r} (r)}{r} = 0

Дифференциальное уравнение второго порядка для массивностенного резервуара

Решение приводит к радиальному напряжению σ_r и касательному напряжению σ_t.

σ_{t} (r) = K + \frac{C}{r^{2}},

σ_{r} (r) = K - \frac{C}{r^{2}}

K, C	Real constants

Радиальное и касательное напряжение толстостенного резервуара

Константы K и C получены с помощью граничных условий.

K = \frac{p_{1} r_{1}^{2} - p_{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}},

C = (p_{1} - p_{2}) \frac{r_{1}^{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}}

Константы K и C

Радиальный прогиб внутреннего и внешнего радиуса открытого резервуара u_r (r₁ ), u_r (r₂ ) можно определить с помощью следующих уравнений:

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

Радиальный прогиб внутреннего и внешнего радиуса резервуара с открытым дном

Параметры RFEM

Смоделировано в программе RFEM 5.06 и RFEM 6.06
Размер элемента l_КЭ = 2,000 мм
Используется изотропная линейная упругая модель материала

Результаты

Результаты RFEM 6 – общий прогиб

Количество	Аналитическое решение	Rfem 6	сечения	RFEM 5	сечения
u_r (r₁ ) [мм]	27,000	26,998	1,000	27,000	1,000
u_r (r₂ ) [мм]	21,750	21,747	1,000	21,750	1,000

504x

13x

Контрольный пример 000064 | 1

;