104x

11-10-2024

VE0064 | Recipiente de pared gruesa

Descripción del trabajo

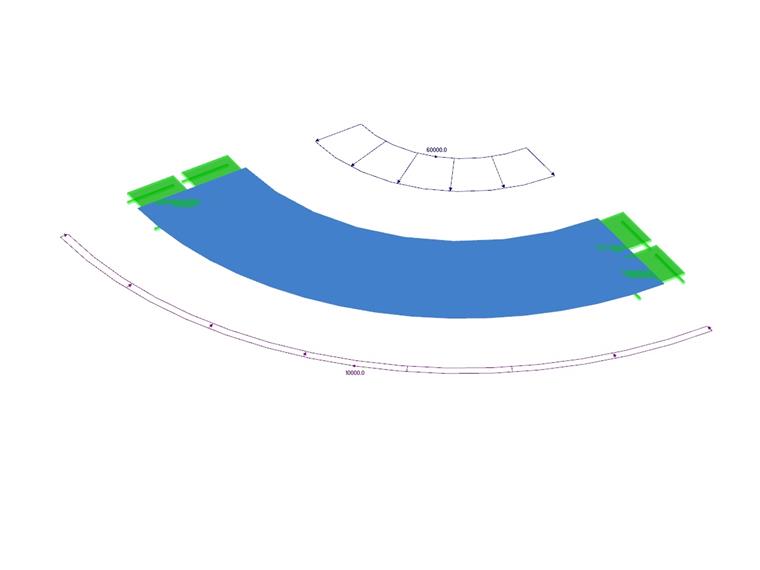
Un recipiente de paredes gruesas está cargado por una presión interna y externa. El recipiente está abierto, por lo que no hay tensión axial. El problema se modela como un modelo de un cuarto. Determine la flecha radial del radio interior y exterior u_r (r₁ ), u_r (r₂ ). Se omite el peso propio.

Material	Elástico	Módulo de elasticidad	E	1,000	MPa
Material	Elástico	Coeficiente de Poisson	ν	0,250	-
Geometría		Radio interior	_r1	200,000	mm
Geometría		Radio exterior	_r2	300,000	mm
Carga		Presión interior	p₁	60,000	kPa
Carga		Presión exterior	_p2	10,000	kPa

Recipiente de pared gruesa

Solución analítica

El estado de tensiones del recipiente de paredes gruesas se describe mediante la ecuación de equilibrio

\frac{d σ_{r}}{d r} + \frac{σ_{r} - σ_{t}}{r} = 0

σ_r	Radial stress
σ_t	Tangential stress

Ecuación de equilibrio para un recipiente de paredes gruesas

Usando las ecuaciones de deformación-deformación y la ley de Hooke, se obtiene la ecuación diferencial de segundo orden

\frac{d^{2} u_{r} (r)}{d r^{2}} + \frac{d u_{r} (r)}{d r} - \frac{u_{r} (r)}{r} = 0

Ecuación diferencial de segundo orden para un depósito de paredes gruesas

La solución conduce a la tensión radial σ_r y la tensión tangencial σ_t.

σ_{t} (r) = K + \frac{C}{r^{2}},

σ_{r} (r) = K - \frac{C}{r^{2}}

K, C	Real constants

Tensión radial y tangencial del recipiente de pared gruesa

Las constantes K y C se obtienen utilizando condiciones de contorno.

K = \frac{p_{1} r_{1}^{2} - p_{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}},

C = (p_{1} - p_{2}) \frac{r_{1}^{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}}

Constantes K y C

La flecha radial del radio interior y exterior del recipiente de extremo abierto ur (_r₁ ), ur (_r₂ ) se puede determinar utilizando las siguientes ecuaciones:

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

Flecha radial del radio interior y exterior del depósito de extremo abierto

Configuración de RFEM

Modelado en RFEM 5.06 y RFEM 6.06
El tamaño del elemento es l_FE = 2.000 mm
Se utiliza el modelo de material elástico lineal isótropo

Resultados

Resultados de RFEM 6 – Deformación total

Cantidad	Solución analítica	RFEM 6	Razón	RFEM 5	Razón
u_r (r₁ ) [mm]	27,000	26,998	1,000	27,000	1,000
u_r (r₂ ) [mm]	21,750	21,747	1,000	21,750	1,000

499x

13x

Ejemplo de verificación 000064 | 1

;