103x

11.10.2024

VE0064 | Réservoir à parois épaisses

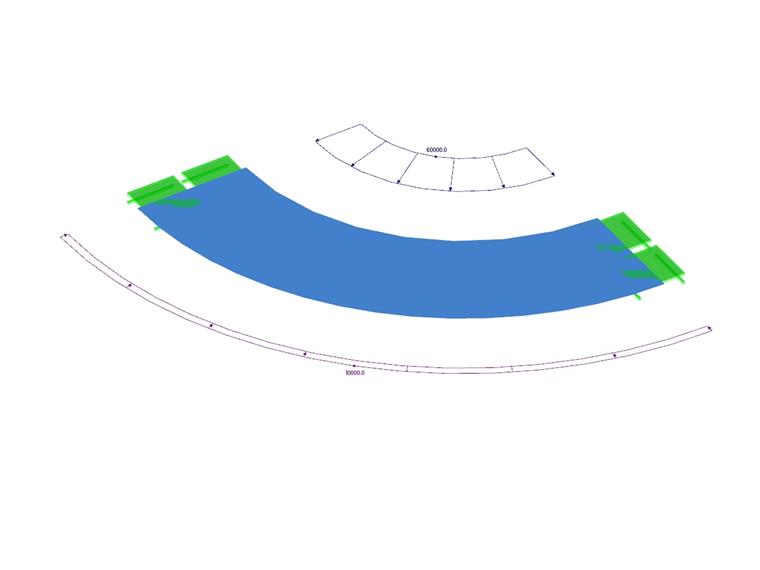
Description du projet

Un réservoir à paroi épaisse est chargé par une pression interne et externe. Les extrémités du réservoir sont ouvertes, il n'y a donc pas de contrainte axiale. Le problème est modélisé sous forme de modèle quart. Déterminer la flèche radiale des rayons interne et externe u_r (r₁ ), u_r (r₂ ). le poids propre est négligé.

Matériau	Résistant	Module d'élasticité	E	1 000	MEP
Matériau	Résistant	coefficient de Poisson	P	0,250
Géométrie		Rayon interne	r₁	200 000	mm
Géométrie		Rayon extérieur	r₂	300 000	mm
Import		Pression interne	P₁	50 000	kPa
Import		Pression externe	P₂	10 000	kPa

Réservoir à parois épaisses

Solution analytique

L'état de contrainte du réservoir à paroi épaisse est décrit par l'équation d'équilibre

\frac{d σ_{r}}{d r} + \frac{σ_{r} - σ_{t}}{r} = 0

σ_r	Radial stress
σ_t	Tangential stress

Équation d'équilibre pour un réservoir à parois épaisses

L'équation différentielle du second ordre est obtenue à l'aide des équations de déformation et de la loi de Hooke

\frac{d^{2} u_{r} (r)}{d r^{2}} + \frac{d u_{r} (r)}{d r} - \frac{u_{r} (r)}{r} = 0

Équation différentielle du second ordre pour un réservoir à paroi épaisse

La solution entraîne la contrainte radiale σ_r et la contrainte tangentielle σ_t.

σ_{t} (r) = K + \frac{C}{r^{2}},

σ_{r} (r) = K - \frac{C}{r^{2}}

K, C	Real constants

Contrainte radiale et tangentielle d'un récipient à paroi épaisse

Les constantes K et C sont obtenues à l'aide des conditions aux limites.

K = \frac{p_{1} r_{1}^{2} - p_{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}},

C = (p_{1} - p_{2}) \frac{r_{1}^{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}}

Constantes K et C

La flèche radiale des rayons intérieurs et extérieurs du réservoir à extrémités ouvertes u_r (r₁ ), u_r (r₂ ) peut être déterminée à l'aide des équations suivantes:

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

Déviation radiale du rayon intérieur et extérieur du récipient à extrémité ouverte

Paramètres RFEM

Modélisé dans RFEM 5.06 et RFEM 6.06
La taille de l'élément est l_EF = 2 000 mm
Le modèle de matériau isotrope linéaire élastique est utilisé

Résultats

Résultats RFEM 6 – Déformation totale

Quantité	Solution analytique	RFEM 6	Ratio	RFEM5	Ratio
u_r (r₁ ) [mm]	27 000	26,998	1 000	27 000	1 000
u_r (r₂ ) [mm]	21,750	21,747	1 000	21,750	1 000

499x

13x

Exemple de vérification 000064 | 1

;