107x

11. Oktober 2024

VE0064 durch | Dickwandiger Behälter

Beschreibung

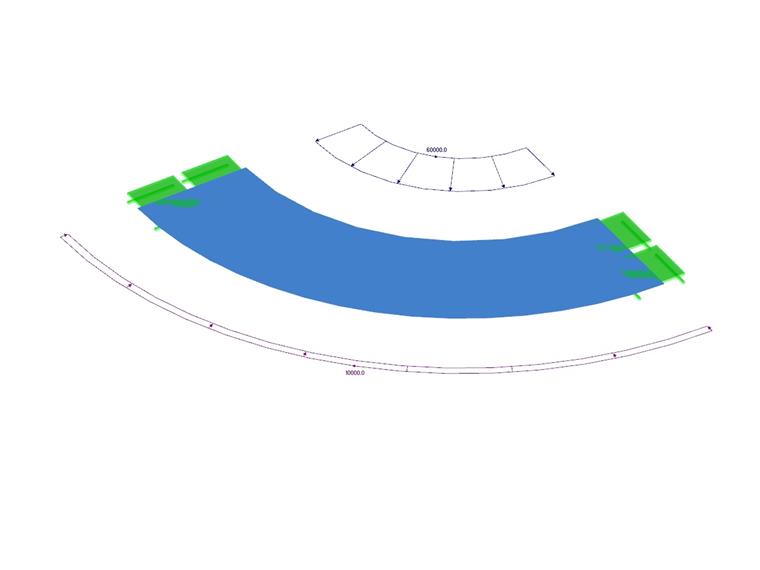
Ein dickwandiger Behälter wird durch inneren und äußeren Druck belastet. Das Ende des Behälters ist offen, folglich gibt es keine Normalspannung. Das Problem wird als Viertelmodell modelliert. Bestimmen Sie die radiale Durchbiegung von Innen- und Außenradius u_r (r₁ ), u_r (r₂ ). Das Eigengewicht wird dabei nicht berücksichtigt.

Material	Elastisch	Elastizitätsmodul	E	1,000	MPa
Material	Elastisch	Querdehnzahl	ν	0,250	-
Geometrie		Innenradius	r<sub>₁ </sub>	200,000	mm
Geometrie		Außenradius	_r2	300,000	mm
Last		Innendruck	p₁	60,000	kPa
Last		Außendruck	p₂	10,000	kPa

Dickwandiger Behälter

Analytische Lösung

Der Spannungszustand des dickwandigen Behälters wird durch die Gleichgewichtsgleichung beschrieben

\frac{d σ_{r}}{d r} + \frac{σ_{r} - σ_{t}}{r} = 0

σ_r	Radial stress
σ_t	Tangential stress

Gleichgewichtsgleichung für einen dickwandigen Behälter

Unter Verwendung der Dehnungs-Durchbiegungs-Gleichungen und des hookeschen Gesetzes erhält man eine Differenzialgleichung zweiter Ordnung

\frac{d^{2} u_{r} (r)}{d r^{2}} + \frac{d u_{r} (r)}{d r} - \frac{u_{r} (r)}{r} = 0

Differenzgleichung II. Ordnung für einen dickwandigen Behälter

Die Lösung führt zur Radialspannung σ_r und Tangentialspannung σ_t.

σ_{t} (r) = K + \frac{C}{r^{2}},

σ_{r} (r) = K - \frac{C}{r^{2}}

K, C	Real constants

Radial- und Tangentialspannung eines dickwandigen Behälters

Mit Hilfe der Randbedingungen erhält man die Konstanten K und C.

K = \frac{p_{1} r_{1}^{2} - p_{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}},

C = (p_{1} - p_{2}) \frac{r_{1}^{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}}

Konstanten K und C

Die radiale Auslenkung des Innen- und Außenradius des offenen Behälters u_r (r₁ ), u_r (r₂ ) kann mit folgenden Gleichungen bestimmt werden:

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

Radiale Durchbiegung des Innen- und Außenradius eines offenen Behälters

RFEM-Einstellungen

Modelliert in RFEM 5.06 und RFEM 6.06
Die Elementgröße beträgt l_FE = 2,000 mm
Es wird ein isotropes linear-elastisches Materialmodell vorausgesetzt.

Ergebnisse

RFEM 6-Ergebnisse – Gesamtdurchbiegung

Anzahl	Analytische Lösung	RFEM 6	Verhältnis	RFEM 5	Verhältnis
u_r (r₁ ) [mm]	27,000	26,998	1,000	27,000	1,000
u_r (r₂ ) [mm]	21,750	21,747	1,000	21,750	1,000

504x

13x

Verifikationsbeispiel 000064 | 1

;