9x

009064

2024-10-11

VE0064 | 厚壁容器

项目介绍

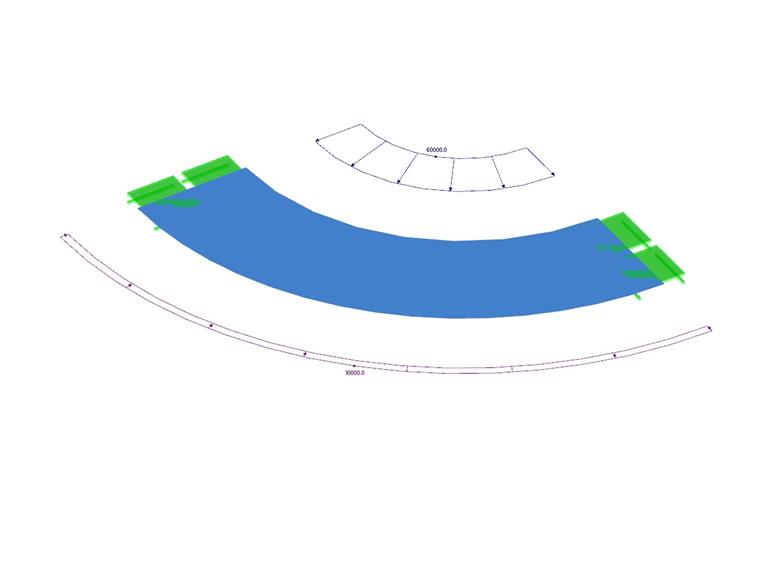
厚壁容器受到内部压力和外部压力。容器底部为开口设计，不产生正应力。该问题采用四分之一模型建模。计算内外半径 u_r (r₁ ) ， u_r (r₂ )的径向挠度。忽略自重。

材料	弹性	弹性模量	E	1.000	MPa
材料	弹性	泊松比	ν	0.250	-
几何尺寸		内弧半径	r₁	200.000	毫米
几何尺寸		外部半径	r·₂	300.000	毫米
荷载		内压	p₁	60.000	kPa
荷载		外部压力	p₂	10.000	kPa

厚壁容器

解析解

厚壁容器的应力状态可以通过径向应力 σ_r和切向应力 σ_t来描述。

σ_{t} (r) = K + \frac{C}{r^{2}},

σ_{r} (r) = K - \frac{C}{r^{2}}

K、C

实常数

厚壁容器的径向和切向应力

常数K和C是在边界条件下获得的。

K = \frac{p_{1} r_{1}^{2} - p_{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}},

C = (p_{1} - p_{2}) \frac{r_{1}^{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}}

两端开口的容器内外半径的径向变形 u_r (r₁ )，u_r (r₂ ) 可以用下面的公式计算：

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

末端开口容器的内外半径的径向挠度

RFEM 设置

在 RFEM 5.06 和 RFEM 6.06 中建模
单元尺寸 l_FE = 2.000 mm
使用各向同性线弹性材料模型

结果

RFEM 6 结果 – 总挠度

RFEM 6 结果 – 总挠度

数量	解析解	RFEM 6	比值	RFEM 5	比值
u_r (r₁ ) [mm]	27.000	26.998	1.000	27.000	1.000
u_r (r₂ ) [mm]	21.750	21.747	1.000	21.750	1.000

验证示例000064 | 1

0x

0x

验证示例000064 | 1

;