104x

2024-10-11

VE0064 | Vaso a parete spessa

Descrizione

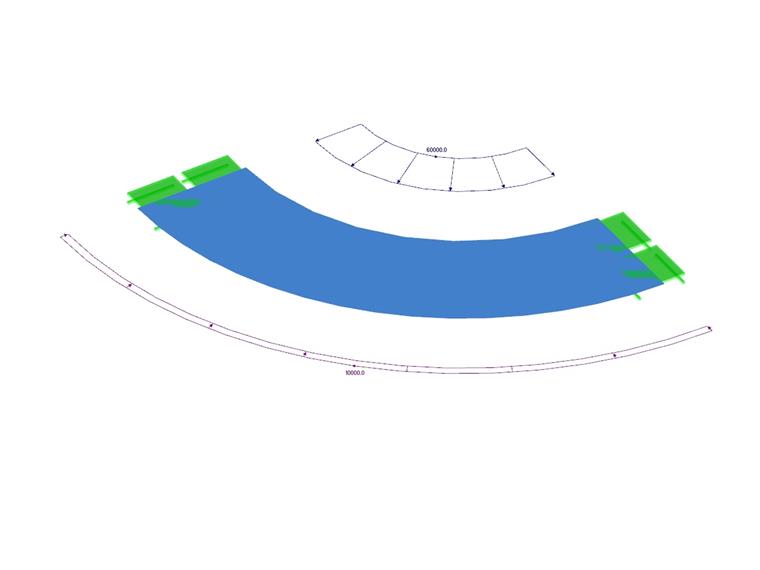
Un recipiente con pareti spesse è caricato dalla pressione interna ed esterna. Il vaso è a estremità aperta, quindi non c'è tensione assiale. Il problema è modellato come un quarto di modello. Determina l'inflessione radiale del raggio interno ed esterno u_r (r₁ ), u_r (r₂ ). Il peso proprio è trascurato.

Materiale	Elastico	Modulo di elasticità	E	1.000	MPa
Materiale	Elastico	Rapporto di Poisson	ν	0,250	-
Geometria		Raggio interno	r₁	200.000	mm
Geometria		Raggio esterno	r₂	300.000	mm
Carico		Pressione interna	p₁	60.000	kPa
Carico		Pressione esterna	p₂	10.000	kPa

Vaso a parete spessa

Soluzione analitica

Lo stato tensionale del vaso a parete spessa è descritto dall'equazione di equilibrio

\frac{d σ_{r}}{d r} + \frac{σ_{r} - σ_{t}}{r} = 0

σ_r	Radial stress
σ_t	Tangential stress

Equazione di equilibrio per recipienti con pareti spesse

Utilizzando le equazioni di deformazione-inflessione e la legge di Hooke, si ottiene l'equazione differenziale del secondo ordine

\frac{d^{2} u_{r} (r)}{d r^{2}} + \frac{d u_{r} (r)}{d r} - \frac{u_{r} (r)}{r} = 0

Equazione differenziale del secondo ordine per recipienti con pareti spesse

La soluzione porta alla tensione radiale σ_r e alla tensione tangenziale σ_t.

σ_{t} (r) = K + \frac{C}{r^{2}},

σ_{r} (r) = K - \frac{C}{r^{2}}

K, C	Real constants

Tensione radiale e tangenziale di un recipiente in parete spessa

Le costanti K e C si ottengono utilizzando le condizioni al contorno.

K = \frac{p_{1} r_{1}^{2} - p_{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}},

C = (p_{1} - p_{2}) \frac{r_{1}^{2} r_{2}^{2}}{r_{2}^{2} - r_{1}^{2}}

Costanti K e C

L'inflessione radiale del raggio interno ed esterno del vaso a estremità aperta u_r (r₁ ), u_r (r₂ ) può essere determinata utilizzando le seguenti equazioni:

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

Inflessione radiale del raggio interno ed esterno di un recipiente con estremità aperta

Impostazioni di RFEM

Modellato in RFEM 5.06 e RFEM 6.06
La dimensione dell'elemento è l_FE = 2.000 mm
Viene utilizzato il modello di materiale elastico lineare isotropo

Risultati

RFEM 6 Risultati – Inflessione totale

Quantità	Soluzione analitica	RFEM 6	Rapporto	RFEM 5	Rapporto
u_r (r₁ ) [mm]	27.000	26.998	1.000	27.000	1.000
u_r (r₂ ) [mm]	21.750	21.747	1.000	21.750	1.000

499x

13x

Esempio di verifica 000064 | 1

;