按照欧洲规范 EN 1993-1-1 计算变截面钢结构柱

系统

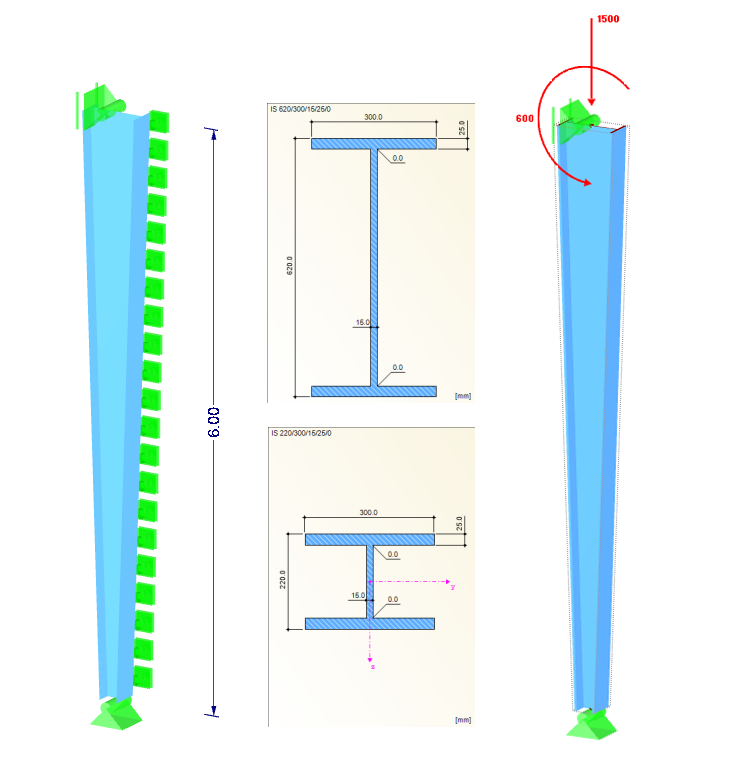
截面： IS 220/300/15/25/0 (柱脚), IS 620/300/15/25/0 (柱头)
材料: S 355 (DIN EN 1993-1-1)
柱高: 6.0 米
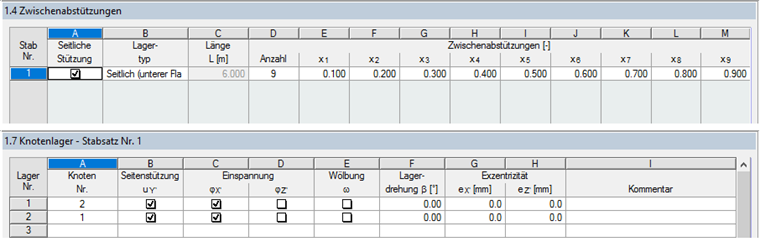
杆件在截面受拉侧沿 Y 方向设置连续支座，

荷载

荷载设计值：
N_Ed = 1.500 kN
M_Ed = 600 kNm

系统

截面分类

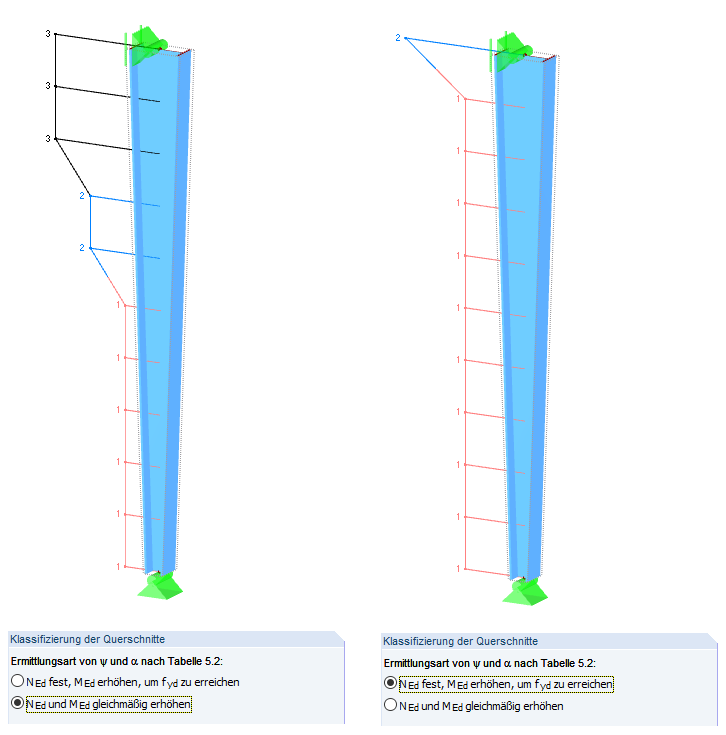
在现有设计荷载下，截面不是承载力极限状态曲线。 因此需要一直增加内力，直到达到承载能力极限状态。
方法有两种：

1. 所有内力线性增加，直到达到承载能力极限状态（见图02左，详细信息中第二个选项[默认]）
2. 仅增加 MEd 直到达到承载能力极限状态（见图 02 [右侧]，详细信息中的第一个选项）

截面分类

这两种选择和方法都会导致非常不同的结果： 从上部三分之一处的最大弹性设计值到整个柱高上可能的塑性设计利用率。

在当前失稳破坏中，轴力没有增加;只有变形和二阶分析引起的弯矩增量。 我们选择第二种方案。

放大系数 α_ult,k最小值

在这种情况下，截面利用率通过线性塑性相互作用确定（见 [2] 公式 [6.2]）。 必须在详细信息中激活该选项，因为附加模块 RF-/STEEL EC3 会按照式（1）对等级 1 或等级 2 的截面进行设计。符合 [2] 中默认的 (6.31) 或 (6.41) 。

根据 [2] 中第 6.3.4(2) 节，在考虑所有缺陷影响和二阶效应分析后，可能需要计算在主平面上达到标准承载力的最小荷载放大系数 αult,k。

对于影响内力的变形，其验算按照 [2] 中公式 (5.1) 进行计算：

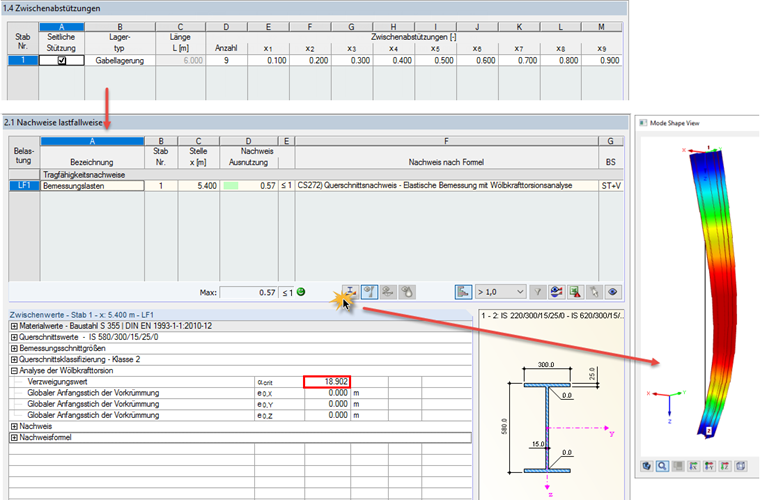
在这种情况下α_cr应由RF-/STEEL EC3和RF-/STEEL Warping Torsion来确定。 最好的方法是生成一个单独的模块工况，并为杆件定义中间侧向约束，以便强制结构第一振型为“在长轴方向上屈曲”。

一阶振型

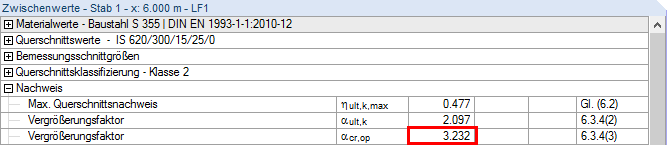
α_cr = 18.90 >10

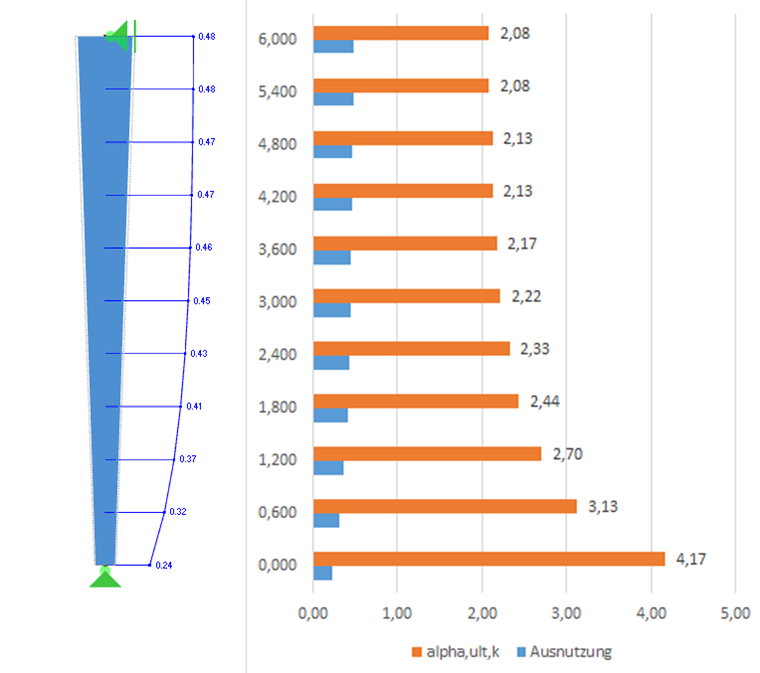
截面设计利用率以及最小荷载放大系数 α_ult,k可以根据一阶静力分析与内力计算得出。 以下是沿杆件长度方向勾选后的利用率和系数：

放大系数和比例

结构构件的长细比和折减系数_cp

确定折减系数 cp 时，长细比_λop考虑弯曲屈曲。 根据 [2] 中公式（6.64）计算：

求解器 RF-/STEEL EC3 按照第 6.3.4 节进行计算，确定满足结构构件在考虑弯扭屈曲弹性临界荷载的作用下的最小荷载放大。 在 Windows 1.4 和 1.7 中的下部结构属性的定义如下。

Beschreibung des statischen Systems

根据参考文献，尽管考虑到底板和柱头上的约束，弹性翘曲约束是合理的，但仍被放弃。 计算结果为:

放大器α_（cr，op）

因此可以按照 [2] 6.3.4 确定结构构件的长细比：

按照表 NA.4，屈曲曲线可以选择按照国家附录（NDP - 6.3.4 [1]）：
屈曲，表 6.2（焊接 I 形截面，t_f < 40 mm，y 方向屈曲）： BC "c"
弯扭屈曲，表 6.4 (h/w = 2.07 > 2): BC "d"

对于组合效应，最小荷载放大系数为：
X_op,z = 0.659 （公式 6.49）
X_op,LT = 0.684 （公式 6.57）
X_op = min {X_op,LT ; X_op,z }
X_op = 0.659

构件设计

实际设计按照 [2] 6.3.4 (2) 公式 (6.63)：