Bemessung einer gevouteten Stütze nach EN 1993-1-1

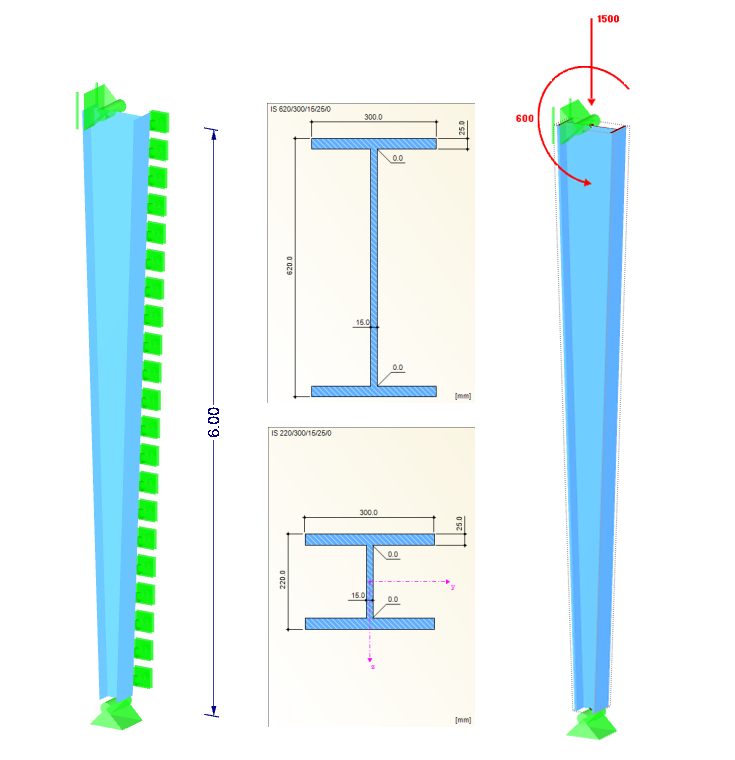
System

Profile: IS 220/300/15/25/0 (Stützenfuß), IS 620/300/15/25/0 (Stützenkopf)
Material: S 355 (DIN EN 1993-1-1)
Stützenhöhe: 6,0 m
Auf der Zugseite des Querschnitts liegt eine kontinuierliche Halterung in Y-Richtung (gebundene Drehachse) vor.

Lasten

Bemessungslasten:
N_Ed = 1.500 kN
M_Ed = 600 kNm

System

uerschnittsklassifizierung

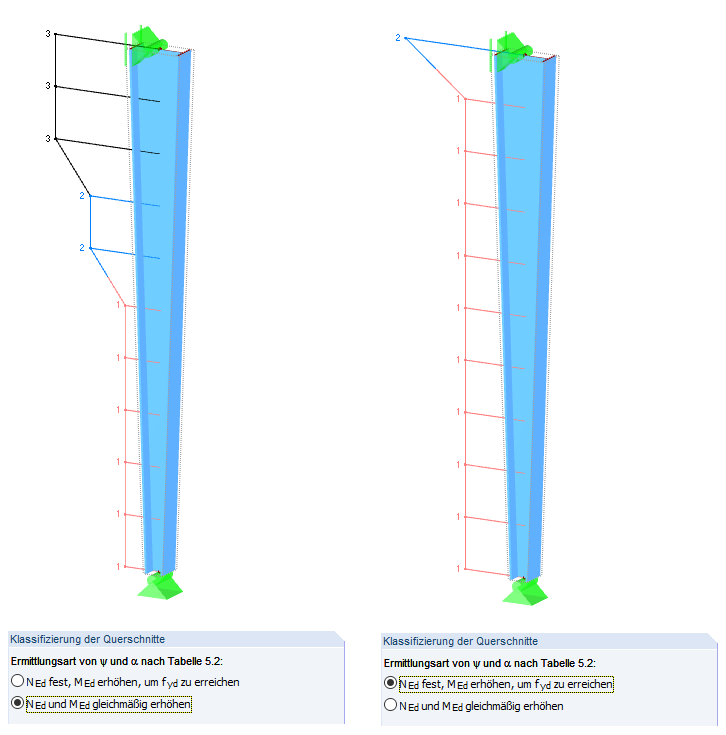
Mit den vorhandenen Bemessungslasten erreicht der Querschnitt nicht die Grenzkurve der Tragfähigkeit. Die Schnittgrößen müssen daher bis zu einem Grenzzustand erhöht werden.
Dafür gibt es zwei Optionen:

1. Alle Schnittgrößen linear erhöhen bis zum Grenzzustand (siehe Bild links, zweite Option (Standard) in den Details)
2. Nur MEd erhöhen zum Erreichen des Grenzzustandes (siehe Bild rechts, erste Option in den Details)

Klassifizierung der Querschnitte

Beide Optionen beziehungsweise Verfahren führen zu recht unterschiedlichen Ergebnissen: von einer im oberen Drittel maximal elastischen Bemessung bis zur komplett möglichen plastischen Querschnittsausnutzung über die gesamte Stützenhöhe.

Beim vorliegenden Stabilitätsversagen ergibt sich keine Erhöhung der Normalkraft, sondern nur ein Zuwachs der Momente infolge von Vorverformungen und der Theorie II. Ordnung. Daher wird die zweite Option gewählt.

Vergrößerungsfaktor α_ult,k

Die Querschnittsausnutzung wird in diesem Fall mit der linearen plastischen Interaktion (siehe [2] Gl. (6.2)) ermittelt. Diese muss in den Details aktiviert werden, da RF-/STAHL EC3 im Falle der QKL 1 oder 2 standardmäßig nach Gl. (6.31) oder (6.41) in [2] nachweisen würde.

Anschließend ist es nach Abschnitt 6.3.4 (2) in [2] gegebenenfalls erforderlich, den kleinsten Vergrößerungsfaktor αult,k bis zum Erreichen der Tragfähigkeit in der Haupttragebene mit allen Effekten aus Imperfektionen und Theorie II. Ordnung zu berechnen.

Die Prüfung, inwieweit die Verformungen einen Einfluss auf die Schnittgrößen haben, erfolgt nach Gleichung (5.1) in [2]:

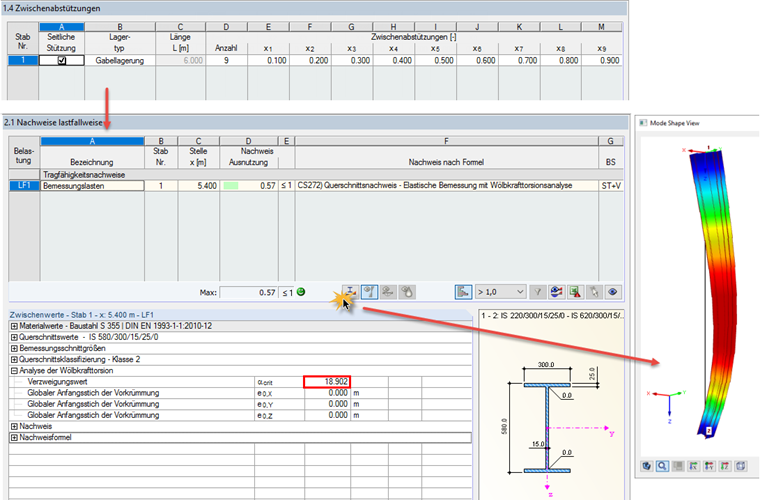
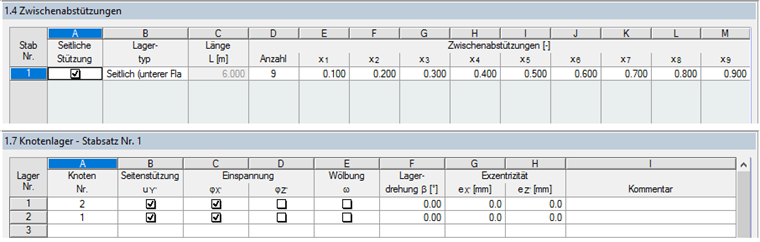
Die Ermittlung von α_cr soll hier mit RF-/STAHL EC3 und RF-/STAHL Wölbkrafttorsion erfolgen. Am besten erzeugt man dazu einen eigenen Modul-Fall und definiert für den Stabsatz Zwischenabstützungen, um die erste Eigenform mit "Knicken in Richtung der starken Achse" zu erzwingen.

Erste Eigenform

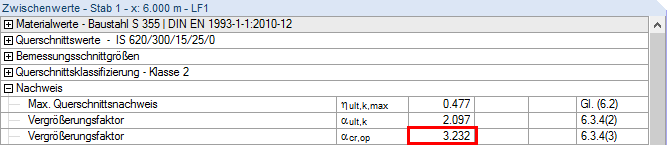
α_cr = 18,90 >10

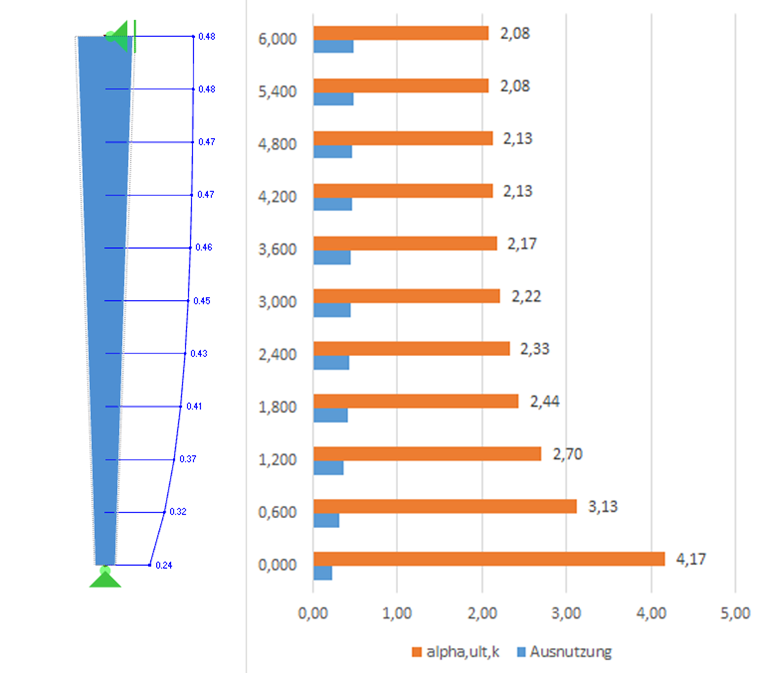
Die Querschnittsausnutzung und damit der Vergrößerungsfaktor α_ult,k können mit den Schnittgrößen nach Theorie I. Ordnung berechnet werden. Es ergeben sich dann über die Stablänge folgende Ausnutzungen und Vergrößerungsfaktoren.

Vergrößerungsfaktoren und Ausnutzungen

Bauteilschlankheit und Abminderungsfaktor χ_op

Zur Ermittlung des Abminderungsfaktors χ_op wird der Schlankheitsgrad λ_op, mit dem Biegeknicken oder Biegedrillknicken aus der Tragwerksebene berücksichtigt wird, benötigt. Dieser berechnet sich nach Gleichung (6.64) in [2] zu:

Beim Nachweis nach 6.3.4 ermittelt ein Eigenwertlöser in RF-/STAHL EC3 den kleinsten Faktor, mit dem die ideale Verzweigungslast mit Verformungen aus der Tragwerksebene erreicht wird. Das zugrunde liegende statische System beschreiben wir in den Masken 1.4 und 1.7 wie folgt.

Beschreibung des statischen Systems

In Anlehnung an die Fachliteratur wurde auf Wölbeinspannungen verzichtet, obwohl diese durch die Fußplatte und sicher auch eine vorhandene am Kopf gerechtfertigt wären. Die Berechnung ergibt:

Vergrößerungsfaktor α_(cr,op)

Es lässt sich damit nach [2] 6.3.4 folgende Bauteilschlankheit ermitteln:

Die Wahl der Knicklinie erfolgt gemäß nationalem Anhang (NDP zu 6.3.4 (1)) nach Tabelle NA.4:
Knicken, Tabelle 6.2 (geschweißtes I-Profil, t_f < 40 mm, Knicken in y): KL "c"
Biegedrillknicken, Tabelle 6.4 (h / b = 2,07 > 2): KL "d"

Bei kombinierter Beanspruchung ist der kleinere Abminderungsfaktor zu verwenden:
χ_op,z = 0,659 (Gl. 6.49)
χ_op,LT = 0,684 (Gl. 6.57)
χ_op = min {χ_op,LT; χ_op,z}
χ_op = 0,659

Bauteilnachweis

Der eigentliche Nachweis erfolgt nun nach [2] 6.3.4 (2) Gleichung (6.63):