Posouzení sloupu s náběhy podle EN 1993-1-1

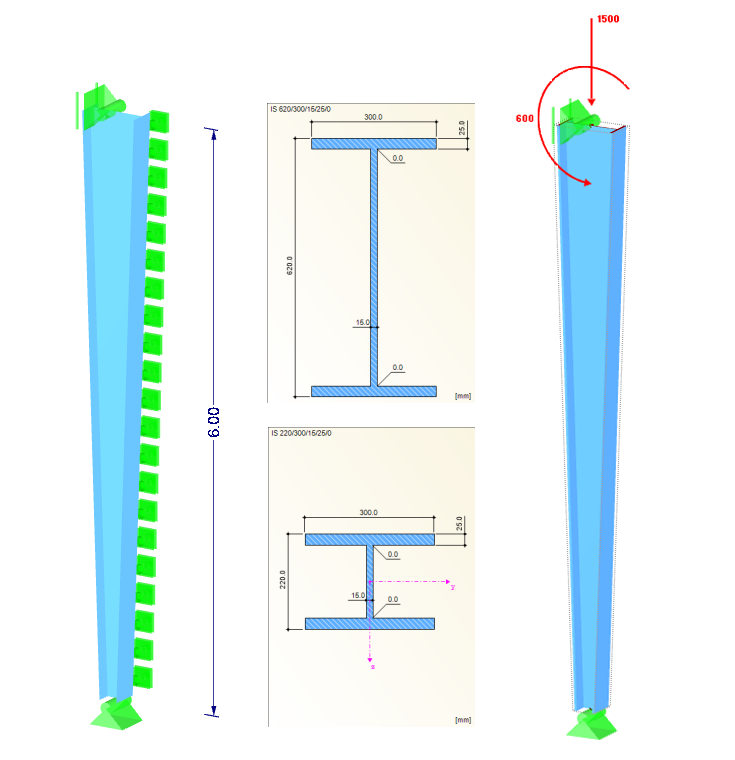
Systém

Průřezy: IS 220/300/15/25/0 (pata sloupu), IS 620/300/15/25/0 (hlava sloupu)
Materiál: S 355 (ČSN EN 1993-1-1)
Výška sloupu: 6,0 m
Na tažené straně průřezu bylo definováno spojité podepření ve směru Y (postranní vetknutí).

Zatížení

Návrhová zatížení:
N_Ed = 1 500 kN
M_Ed = 600 kNm

Systém

Klasifikace průřezů

Při působení návrhových zatížení nedosáhne průřez mezní křivky únosnosti. Vnitřní síly se tak musí zvýšit až do dosažení mezního stavu.
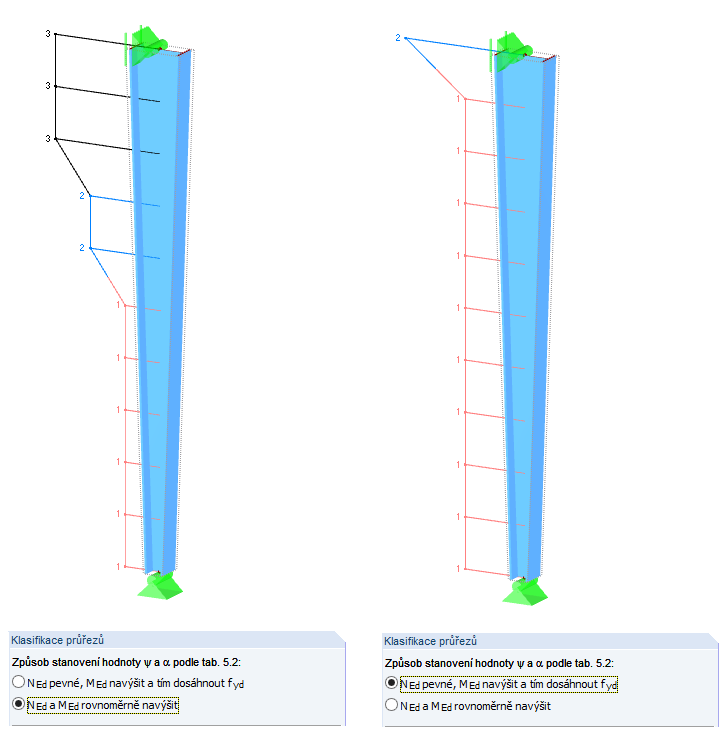
Nabízí se přitom dvě možnosti:

1. Rovnoměrně navýšit všechny vnitřní síly až do dosažení mezního stavu (viz obrázek vlevo, druhá (standardní) volba při nastavení detailů posouzení)
2. Navýšit pouze MEd až do dosažení mezního stavu (viz obrázek vpravo, první volba při nastavení detailů)

Klasifikace průřezů

Obě volby, respektive oba postupy vedou ke značně odlišným výsledkům: od ověření maximální pružné únosnosti v horní třetině sloupu až po možné plastické využití průřezu po celé výšce sloupu.

Při stabilitním selhání tu nedochází ke zvýšení normálové síly, pouze k nárůstu momentů vlivem počátečních přetvoření a analýzy druhého řádu. Proto zvolíme druhou možnost.

Nejmenší násobitel α_ult,k

Při výpočtu využití průřezu se v tomto případě uvažuje lineárně plastická interakce (viz [2], rovnice (6.2)). Je třeba ji aktivovat v nastavení detailů, protože v modulu RF-/STEEL EC3 se pro posouzení průřezů třídy 1 nebo 2 standardně používá rovnice (6.31) nebo (6.41) normy [2].

Následně může být v některých případech nezbytné podle článku 6.3.4. (2) normy [2] vypočítat nejmenší násobitel návrhového zatížení αult,k, při kterém se dosahuje charakteristická únosnost při namáhání průřezu v rovině, ale bez uvažování vzpěru z roviny nebo klopení. Přitom se však uvažují všechny příslušné účinky globálních a místních deformací a imperfekcí v rovině.

Do jaké míry deformace ovlivňují vnitřní síly, ověříme na základě rovnice 5.1 normy [2]:

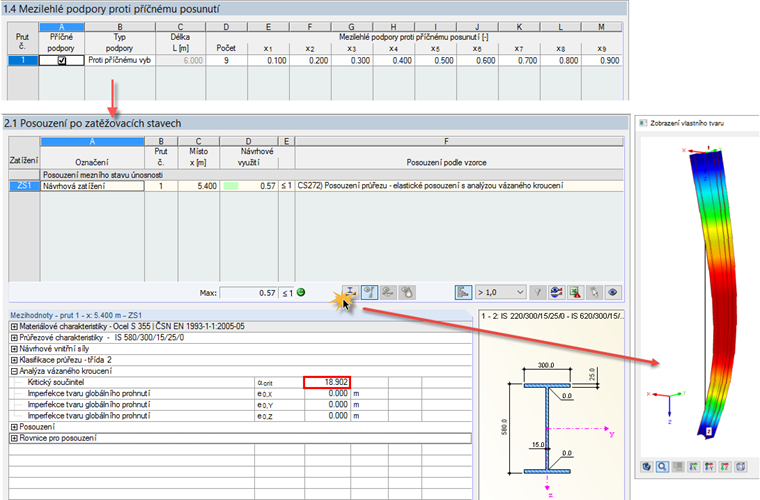
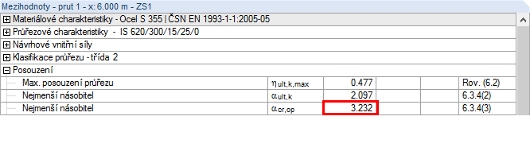
Hodnotu α_cr vypočítáme pomocí modulu RF-/STEEL EC3 a jeho rozšíření RF-/STEEL Warping Torsion. Nejlépe bude vytvořit si v modulu samostatný případ a zadat mezilehlé podpory pro sadu prutů, abychom dosáhli prvního vlastního tvaru s „vybočením ve směru osy s větší tuhostí“.

První vlastní tvar

α_cr = 18,90 >10

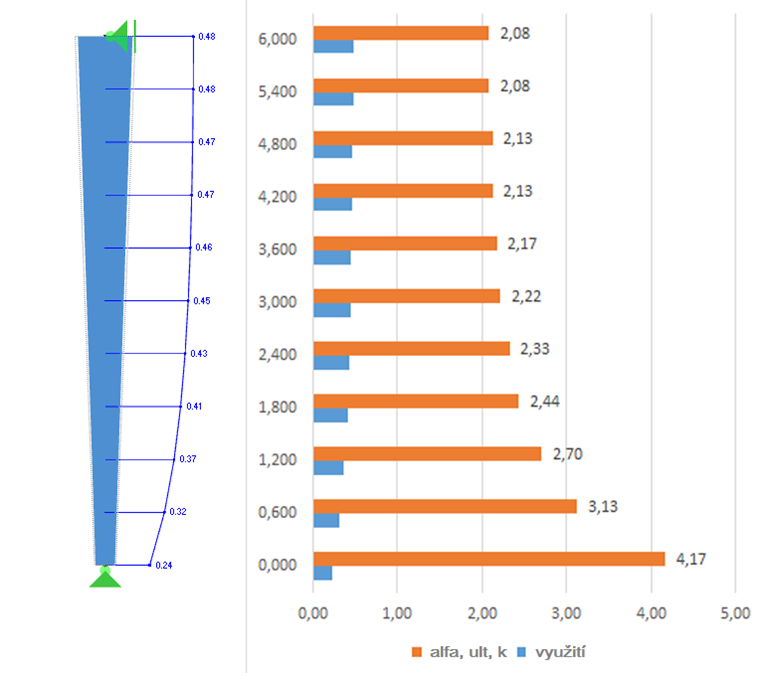
Při výpočtu využití průřezu a tím také nejmenšího násobitele α_ult,k můžeme vycházet z vnitřních sil podle teorie prvního řádu. Po délce průřezu se tak stanoví následující využití a nejmenší násobitele návrhového zatížení.

Faktory a poměry rozšíření

Štíhlost konstrukčního prvku a součinitel vzpěrnosti χ_op

Pro výpočet součinitele vzpěrnosti χ_op je zapotřebí poměrná štíhlost λ_op, zohledňující vzpěr z roviny a klopení. Stanoví se z výrazu (6.64) v [2]:

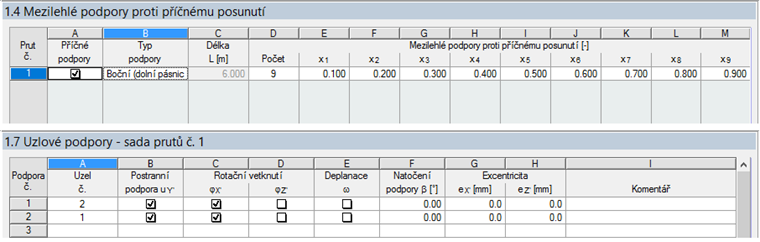
Při posouzení podle 6.3.4 vypočítá modul RF-/STEEL EC3 hodnotu nejmenšího násobitele, při kterém bude dosažena pružná kritická únosnost dílce, stanovená s ohledem na vzpěr z roviny a klopení. Vychází se přitom ze statického systému, který popíšeme v dialozích 1.4 a 1.7.

Beschreibung des statischen Systems

S odvoláním na příslušnou odbornou literaturu nezadáme vetknutí proti deplanaci, ačkoli by ho opodstatňovala patní deska a také vetknutí v hlavě sloupu. Výsledek výpočtu je znázorněn na následujícím obrázku:

Násobitel α_(cr,op)

Podle [2], čl. 6.3.4 tak lze stanovit následující poměrnou štíhlost konstrukčního prvku:

Křivku vzpěrné pevnosti zvolíme v souladu s tabulkou 6.2 a 6.4 normy [2]:
Vzpěr, tabulka 6.2 (svařovaný I-průřez, t_f < 40 mm, vzpěr v y): vzpěrnostní křivka „c“
Klopení, tabulka 6.4 (h / b = 2,07 > 2): křivka klopení „d“

Při kombinovaném namáhání je třeba použít menší součinitel vzpěrnosti:
χ_op,z = 0,659 (rovnice 6.49)
χ_op,LT = 0,684 (rovnice 6.57)
χ_op = min {χ_op,LT; χ_op,z}
χ_op = 0,659

Posouzení konstrukčního prvku

Vlastní posouzení se nyní provede podle [2], čl. 6.3.4 (2), rovnice (6.63):