墙体刚度的计算可以参考第二篇文章。
1
建筑物
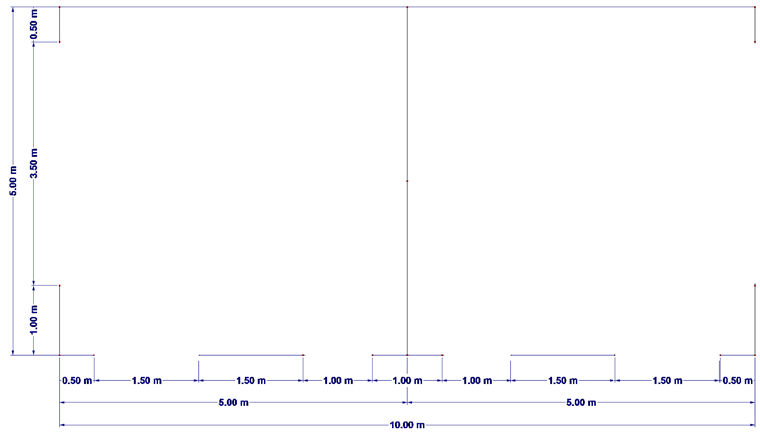
平面图
由于墙体刚度的不同，墙体刚度对楼板的总变形有很大的影响。 此外，墙体的非对称布置也会影响建筑物的变形。
这种影响通常通过二维位置的刚度来考虑。
示例
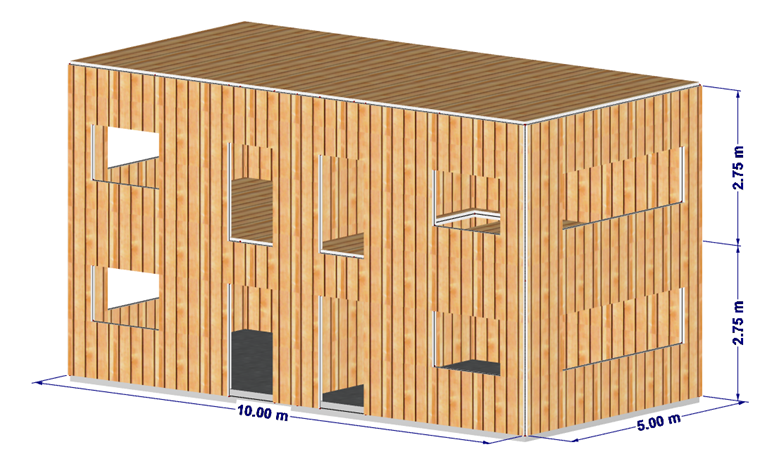
我们在一个简单的两层建筑中展示了这种效应。 该建筑的平面图很规则。 关于最小刚度刚度准则的更多信息请参见 [1]。
1
建筑物
系统
- 平面图 = 5 m ⋅ 10 m
- 简化计算，不包括窗户在内。
- 在墙的两端各放置一个拉杆。
- 墙体结构和刚度如本系列文章 2 中所述。
- 有限元网格尺寸 = 1.5 m
2
平面图
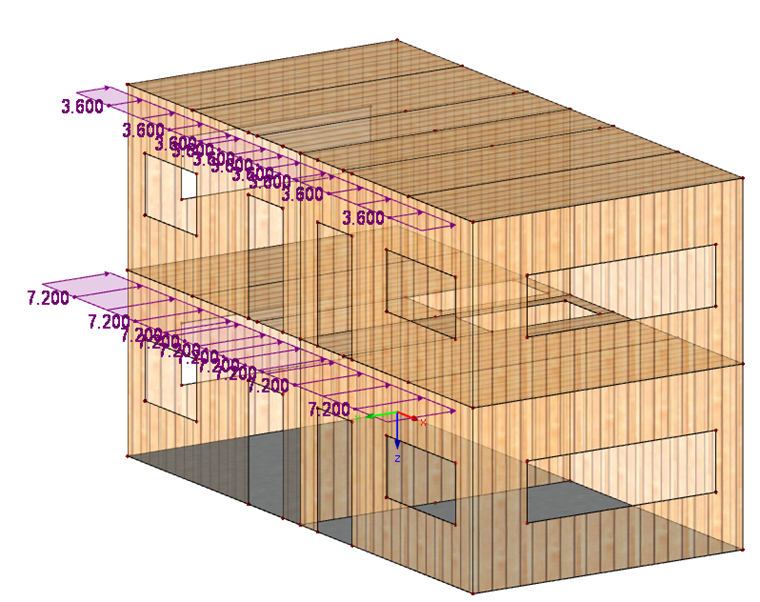
荷载工况/结果组合
- 自重和结构 = 2 kN/m²
- 全局 y 方向风荷载
- 武井2
- 高度=海拔100 m NN
- we+d = 0.46 + 0.74 = 1.2 kN/m²
- We,d = 1.2 kN/m² ⋅ 3 m = 3.6 kN/m
3
风荷载
组合
- CO1 = 1.0 LC1 + 1.5 LC2
墙刚度
这样就会产生四种不同的墙体长度。 为了简化计算，墙体刚度会被等效杆件计算。 刚度的确定同上一篇文章一样。
| 剪力墙 | 长度[m] | 弹性模量 [kN/cm²] | D66/D77 [kN/cm] | G 模量 [kN/cm²] | D88 [kN/cm] | 刚度支座 [kNcm/rad] |
|---|---|---|---|---|---|---|
| 1 | 0.5 | 792 | 9,504 | 0.47 | 6.5 | 64,499 |
| 2 | 1.0 | 396 | 4,752 | 0.80 | 11,0 | 257,995 |
| 3 | 1.5 | 264 | 3,168 | 1,04 | 14,3 | 580,489 |
| 4 | 2.5 | 158 | 1,901 | 1,36 | 18,8 | 1.612.469 |
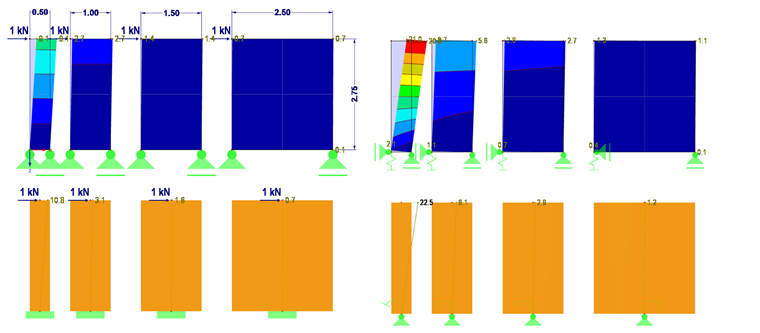
程序会根据这四种墙体长度来计算墙体刚度。 每面墙施加 1 kN 的单位荷载。 因为长度超过 2.5 m 和高度为 2.75 m 的墙体不可能制造，所以在中间将中间墙体划分开。
在附件 RFEM 模型文件 1 中，计算了所有墙长度上的变形，作为面和杆件的结果。 模型的上半部分是在没有设置墙锚固件的情况下计算的，下半部分是使用墙锚固件计算的。 图 04 中也对变形进行了比较。
由计算得出的每面墙的变形可以计算出每面墙的刚度。
例如，墙 1 长度为 50 cm，刚度如下：
C = F/u = 1 kN/22,5mm = 0,044 kN/mm
c = F/l ⋅ C = 1 kN/0.5 m ⋅ 0.044 kN/mm = 0.088 N/mm²
对于所有墙：
- 墙 | l = 0.5 m | c = 0.088 N/mm²
- 墙 | l = 1.0 m | c = 0.164 N/mm²
- 墙 | l = 1.5 m | c = 0.230 N/mm²
- 墙 | l = 2.5 m | c = 0.333 N/mm²
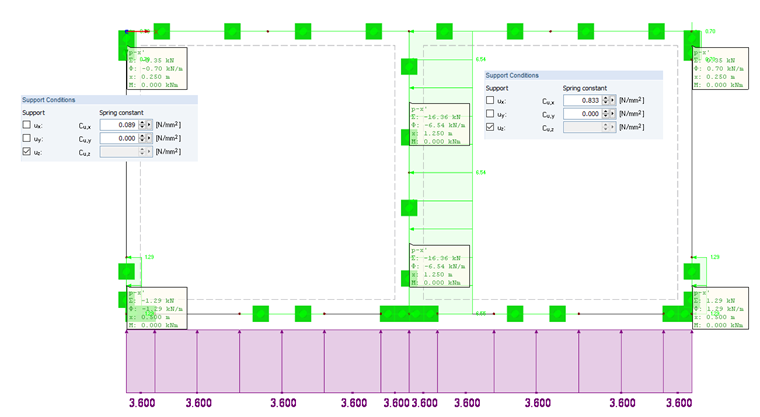
这些刚度在平面图上被分配给相应的线支座（见图 05）。 在随附的 RFEM 模型文件 2 中可以找到平面图。
5
支座反力和刚度
由于建筑物是对称的，所以不存在建筑物旋转。 本文对此进行了更详细的介绍：
所附视频显示了在非对称平面图中水平力是如何与荷载方向发展的。
概述总结
本文介绍了对木板结构的计算。 用户可以使用面单元或杆件单元来确定面的刚度。 考虑锚固产生的弹性。
请使用随附的 Excel 文件重新进行示例的计算。
本系列教程的最后一部分，由线支座反力确定反力的验算（见图 05）。
