变形的计算涉及到本系列的第一篇文章。
1
系统
墙的刚度
墙的刚度是在1 kN的单位荷载下计算的。有关此处使用的方程的进一步信息,请参见提供的 文献 [1] 以及本系列先前提到的文章。
示例
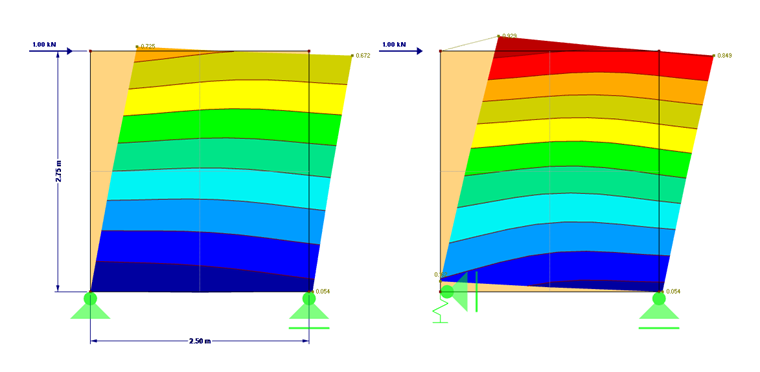
刚度计算通过图01中显示的尺寸来进行一个简单的示例。
2
系统
系统
- 墙长 l = 2.50 m
- 墙高 h = 2.75 m
- 立柱 C24 6/12 cm, ρm,T = 350 kg/m³
- OSB 3, t = 18 mm (单面), ρm,O = 439 kg/m³, G = 108 kN/cm²
- kser = 159N/mm
- bE = b+t = 12cm + 1.8cm = 13.8 cm
- 钉 d = 1.5 mm, t = 45 mm
- 钉距 av = 60 mm (单行)
- 网格 62.5 cm
- 固定螺栓用10个直径4.2 mm的钉固定
- FE网格大小为 1.3m(每片有4个元素)
刚度
- 连接件(钉)的柔度:
- 覆盖板的柔度:
- 肋的柔度:
- 锚的柔度:
- 柔度总和(不考虑锚):
转换为有效面积
计算的刚度转换为有效的正交各向异性板刚度。关于正交各向异性材料模型的背景信息可以在本文中找到。
- 常规刚度部分:
- 板平面内的剪切刚度:
锚可以在 RFEM 中直接定义为线性弹性弹簧,其弹簧刚度6,879.9 N/mm。在图1中显示了变形的比较。附加模型1中也可以看到差异。
对于三维计算而言,该方法在于定义板弯曲刚度上存在问题。关于正交各向异性材料模型的专文对此进行了详细介绍。
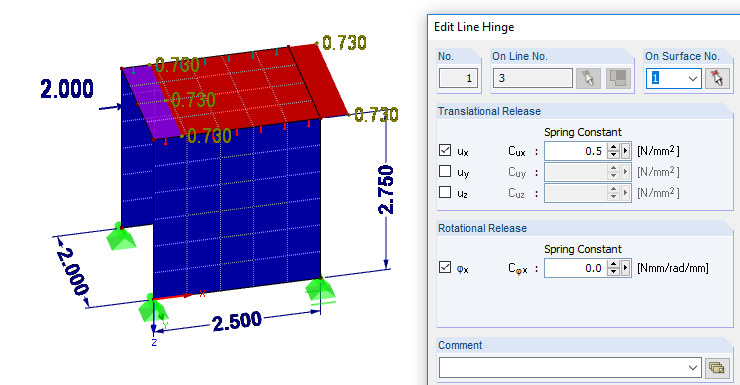
而不是通过面积来反映木板墙的刚度,在接下来的方法中,将计算的柔度转换为线关节进行说明。
3
空间模型
其优点在于可以将模型的表面特性视为刚性。
总结
在本文中,展示了通过有效的正交各向异性表面来计算木板。锚可以被直接定义为弹簧刚度。对于系统的二维线性计算,结果与 [1] 中的手工计算非常吻合。可进行实际的刚度计算。示例模型在下载中提供。
作为另一种选择,展示了将柔度转换为线性弹簧的线方法。对于空间模型,该方法更适合,因为它基本上排除了板弯及板面内弯的影响。对于此,此下载中也提供了模型。
在另一篇文章中,将展示平面图的2D抗震以及3D墙体板的计算。