Fundamentação teórica
O movimento vibratório de um sistema mecânico inicialmente não perturbado e depois excitado harmoniosamente, consiste numa vibração natural amortecida com amplitude decrescente e numa vibração forçada com amplitude constante. O processo transitório e o estado estacionário são descritos na seguinte fórmula.
|
t |
Zeit |
|
ω |
Erregerkreisfrequenz |
|
ωD |
Eigenkreisfrequenz |
|
ζ |
Dämpfung |
|
A |
Konstante |
|
B |
Konstante |
|
C |
Konstante |
|
D |
Konstante |
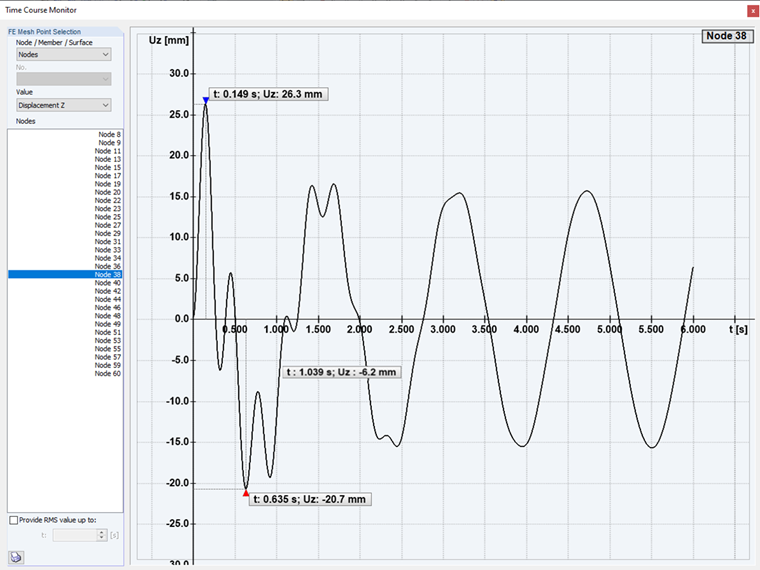
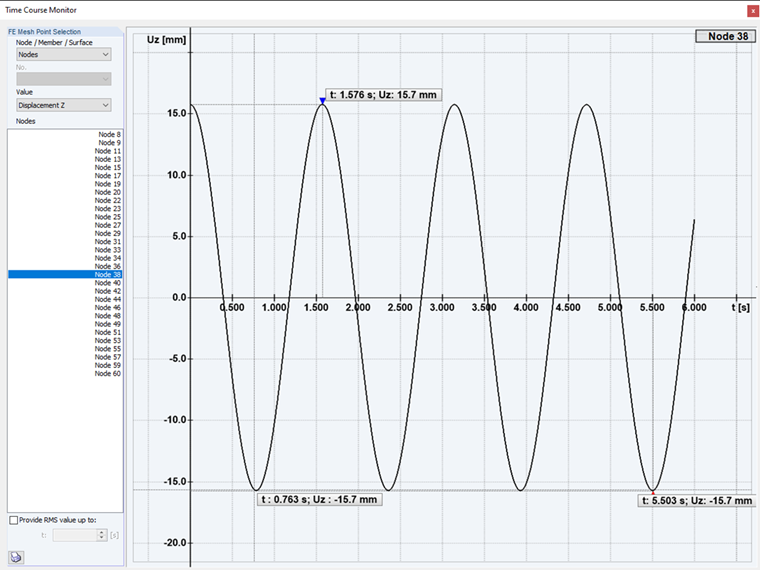
Se a relação de frequência for η < 1, o que é designado como excitação subcrítica, a vibração forçada é mais lenta do que a vibração natural amortecida e ocorre um processo transitório. Após alguns períodos de amortecimento da vibração natural, o sistema é sintonizado para a vibração forçada mais lenta que, em última análise, continua a ser o único componente de vibração.
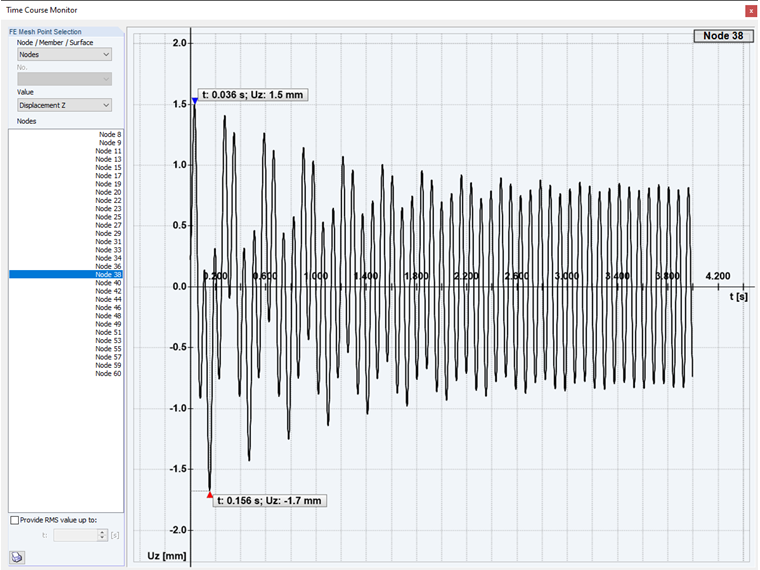
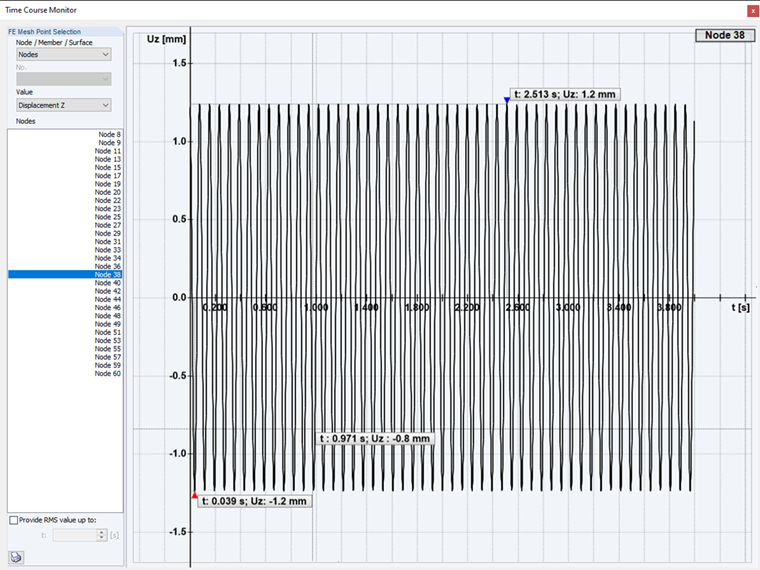
Se o caso é η > 1, agora chamado de excitação supercrítica, a vibração forçada é maior em frequência do que a vibração natural amortecida. Agora, a oscilação harmónica rápida ocorre em torno da oscilação natural mais lenta e amortecida até esta desaparecer completamente e, novamente, apenas permanecer o componente de vibração forçada pela excitação.
Uma vez que existe um amortecimento em todos os casos práticos, o que leva ao desvanecimento da vibração natural, é apenas de interesse, independentemente da relação de frequência, considerar e analisar adicionalmente o respetivo movimento de vibração forçada restante (parte do estado estacionário). Este movimento vibratório é designado por vibração (quase) estacionária e o estado correspondente do sistema é designado por estado estacionário.
A vibração natural tem a frequência angular ωD do sistema amortecimento, enquanto que o componente de vibração forçado pela excitação tem a frequência angular ω da excitação harmónica. Assim, a vibração global, que resulta da sobreposição destas duas vibrações parciais, segue uma direcção cuja ocorrência depende em grande medida da relação ω/ωD ; ou seja, na relação de frequências η.
Exemplo
O comportamento transitório é descrito a seguir, utilizando uma estrutura de aço. É assumido que esta estrutura é harmonicamente excitada. Na estrutura, são geradas excitações harmónicas para mostrar os diferentes processos transitórios. Para melhor corresponder a frequência da excitação harmónica com a estrutura, é primeiro criado um caso de vibração natural através do DYNAM Pro - Natural Vibrations. Como simplificação, apenas as formas próprias na direção Z global são consideradas nos casos de vibração natural.
Excitação subcrítica: No primeiro caso da análise de histórico de tempo, é realizada uma excitação subcrítica da estrutura. Com uma frequência de excitação inferior à forma própria.
Excitação supercrítica: No segundo caso da análise de histórico de tempo, é realizada uma excitação supercrítica da estrutura. Com uma frequência de excitação superior à forma própria.
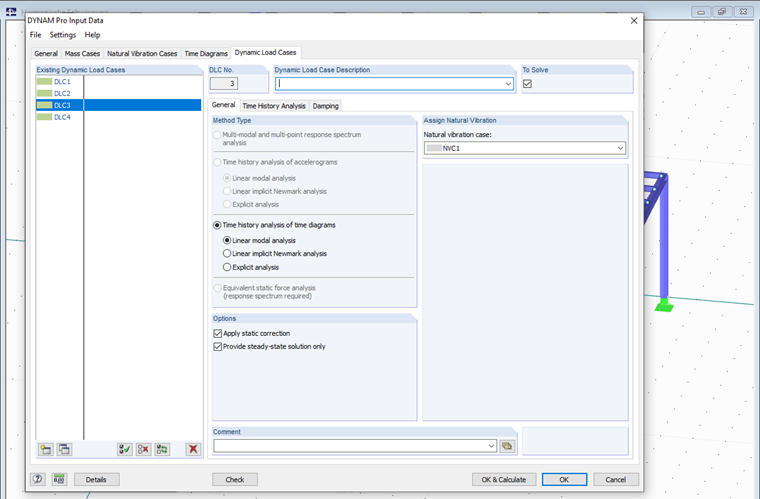
No terceiro e quarto casos, utilizamos a opção de módulo adicional para uma solução do estado estacionário para os dois casos de excitação criados anteriormente. Ao fazer isso, o estado estacionário é definido diretamente. Também é geralmente conhecido como estado estacionário.