Podstawy teoretyczne
Drgania układu mechanicznego, który jest początkowo niewzbudzony, a następnie poddany oddziaływaniu harmonicznemu, składa się z tłumionych drgań własnych o malejącej amplitudzie oraz drgań wymuszonych o stałej amplitudzie. Odpowiedź przejściowa i tzw. stan ustalony („steady state”) są opisane przez poniższy wzór.
| t | Czas |
| ω | Częstotliwość kątowa wzbudzenia |
| ωD | częstość kątowa |
| ζ | tłumienie |
| [LinkToImage04] | Stały |
| B | Stały |
| C | Stały |
| D | Stały |
| η | Stosunek częstotliwości |
| γM[LinkToImage09] | Częściowy współczynnik bezpieczeństwa dla nośności przekroju |
| ωD | częstość kątowa |
Jeżeli stosunek częstotliwości η Po kilku szybkich cyklach tłumionych drgań własnych cały układ przechodzi w stadium wolniejszych drgań wymuszonych, które ostatecznie pozostają jedyną składową drgań.
Jeżeli η 1, co nazywa się wzbudzeniem nadkrytycznym, drgania wymuszone mają większą częstotliwość niż tłumione drgania własne układu. Dochodzi do szybkich oscylacji harmonicznych nakładających się na wolniejsze, tłumione drgania własne. Trwa to do momentu, gdy składowa drgań własnych ulegnie całkowitemu wygaszeniu i ponownie pozostanie tylko składowa drgań wymuszona przez wzbudzenie.
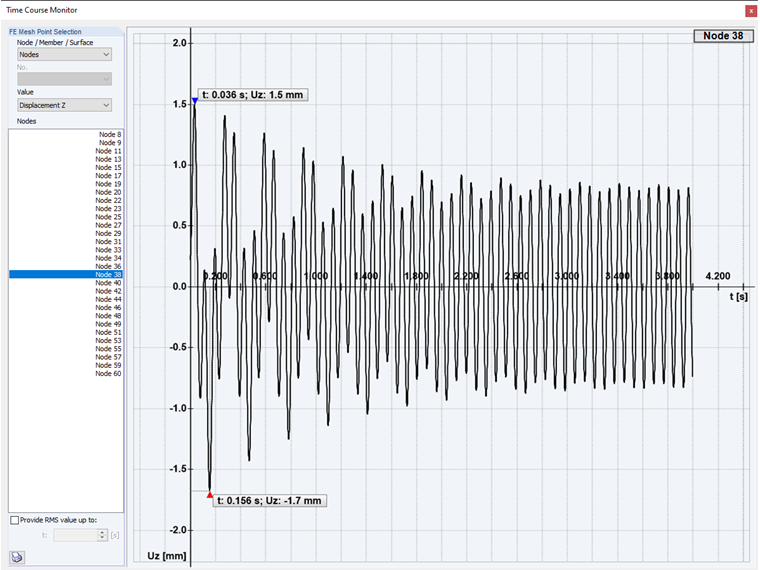
Ponieważ praktycznie w każdej konstrukcji występuje tłumienie, które prowadzi do zaniku drgań własnych, interesujące jest analizowanie jedynego pozostałego ruchu - drgań wymuszonych. Ten ruch drgający nazywany jest drganiami (quasi) stacjonarnymi, a odpowiadającym im stanem jest tzw. stanem ustalonym.
Drgania własne mają częstotliwość kątową ωD tłumionego układu, a składowa drgań wymuszonych przez wzbudzenie ma częstotliwość kątową ω wzbudzenia harmonicznego. W ten sposób drgania całkowite wynikające z superpozycji tych dwóch drgań częściowych przyjmują przebieg, którego wygląd zależy silnie od proporcji ω/ωD, czyli od stosunku częstotliwości η.
Przykład
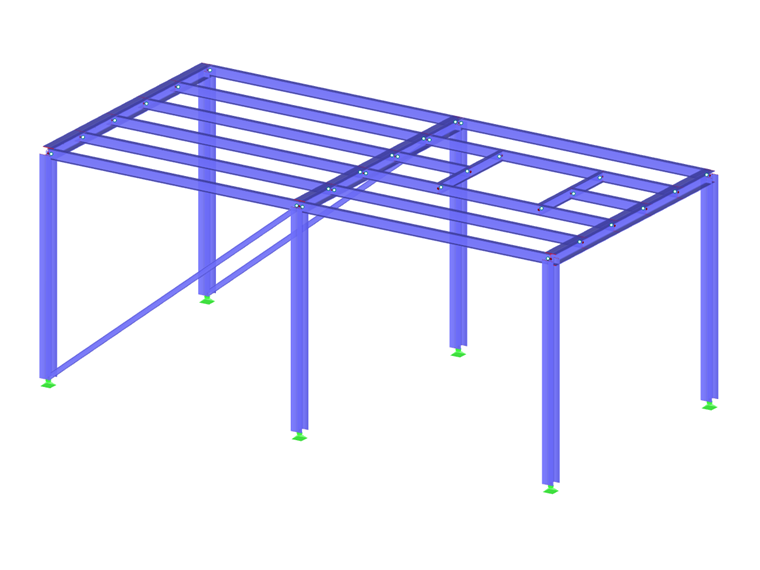
Poniżej wyjaśniono zachowanie odpowiedzi przejściowej przy użyciu konstrukcji stalowej. Zakłada się, że konstrukcja ta jest wzbudzana harmonicznie. W tym celu do konstrukcji przykładane są wzbudzenia harmoniczne, ukazujące różne efekty przejściowe. W celu lepszego dopasowania częstotliwości wzbudzenia harmonicznego do konstrukcji najpierw generowany jest przypadek drgań własnych za pomocą programu DYNAM Pro - Natural Vibrations. Dla uproszczenia, w przypadkach drgań własnych uwzględniane są tylko kształty drgań własnych w globalnym kierunku Z.
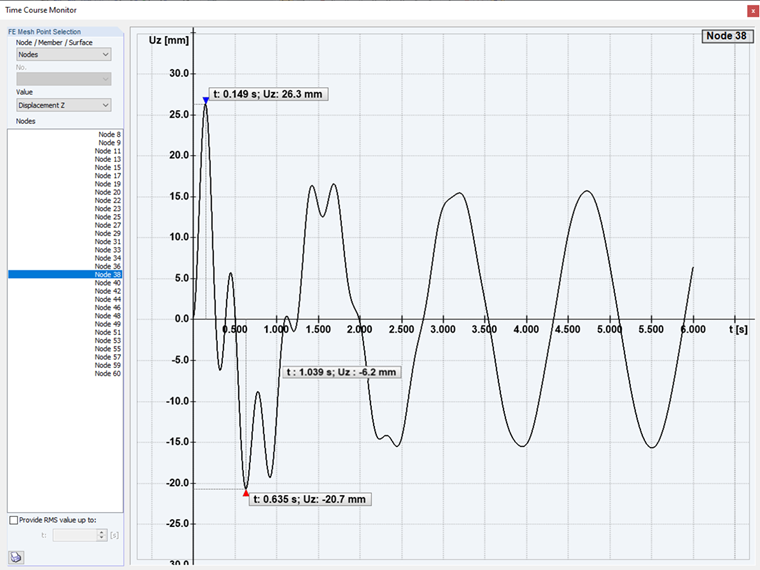
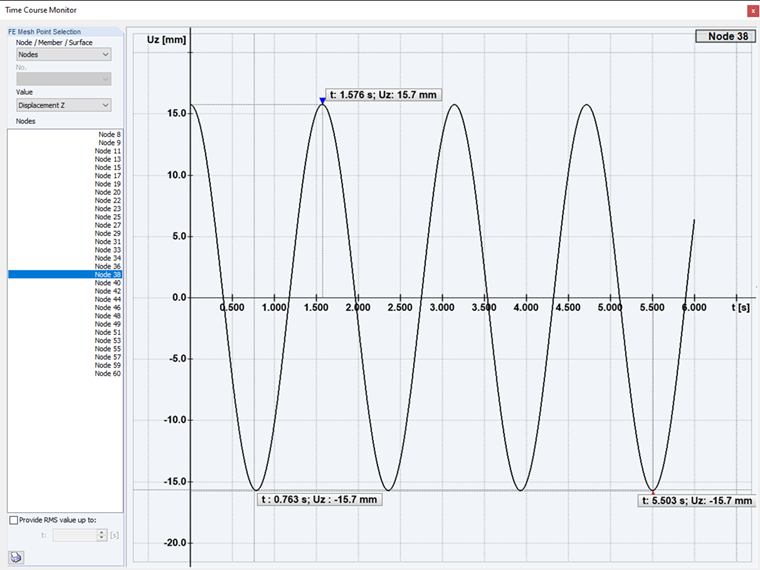
Wzbudzenie podkrytyczne: W pierwszym przypadku analizy czasowej zachodzi wzbudzenie podkrytyczne konstrukcji. Częstotliwość wzbudzenia jest mniejsza niż kształt drgań własnych.
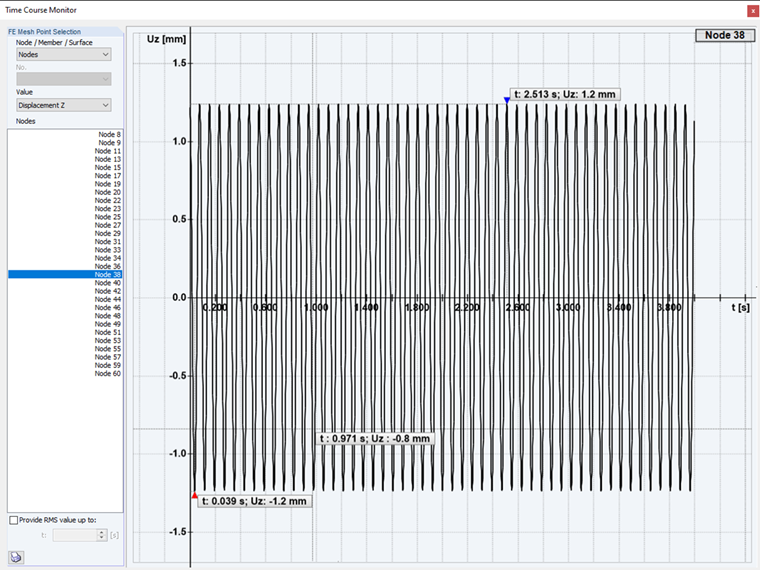
Wzbudzenie nadkrytyczne: W drugim przypadku analizy czasowej następuje tak zwane nadkrytyczne wzbudzenie konstrukcji. Częstotliwość wzbudzenia jest większa niż kształt drgań własnych.
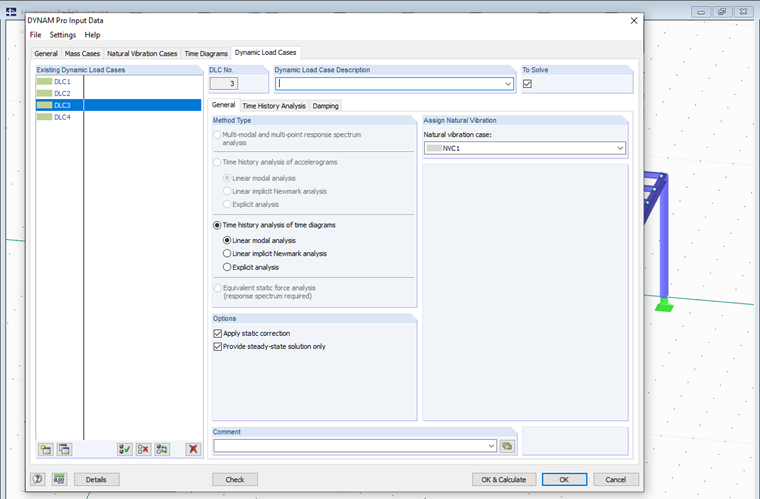
W trzecim i czwartym przypadku DYNAM Pro - Forced Vibrations wykorzystano opcję modułu dodatkowego dotyczącą stanu ustalonego dla dwóch poprzednio utworzonych przypadków. Uzyskujemy w ten sposób bezpośrednio postać drgań ustalonych. Jest on również ogólnie nazywany stanem ustalonym.
