Base teorica
Il movimento vibrazionale di un sistema meccanico inizialmente indisturbato, poi armonicamente eccitato è costituito da una vibrazione naturale smorzata con ampiezza decrescente e da una vibrazione forzata con ampiezza costante. Il processo transitorio e lo stato stazionario sono descritti nella seguente formula.
| t | Tempo |
| ω | Frequenza angolare di eccitazione |
| ωd | frequenza angolare |
| ζ | smorzamento |
| [LinkToImage01] | Costante |
| B | Costante |
| C | Costante |
| d | Costante |
| η | Rapporto di frequenza |
| γM[LinkToImage04] | Coefficiente di sicurezza parziale per la resistenza della sezione trasversale |
| ωd | frequenza angolare |
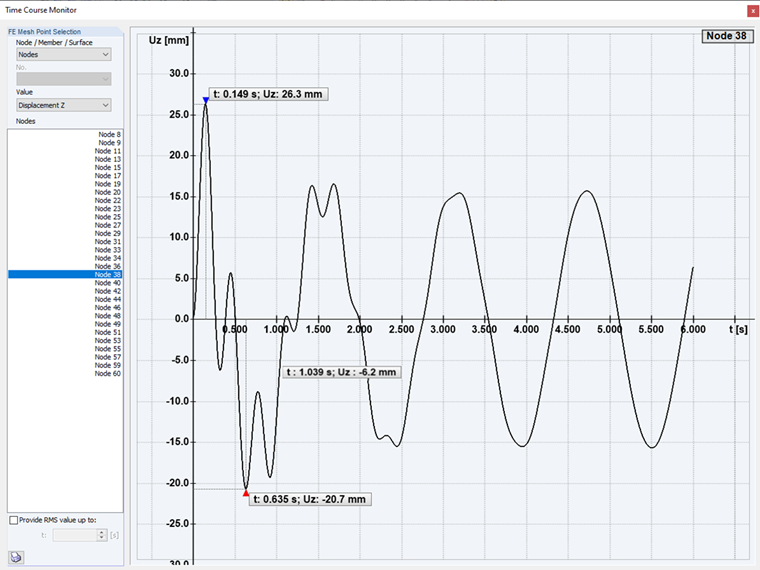
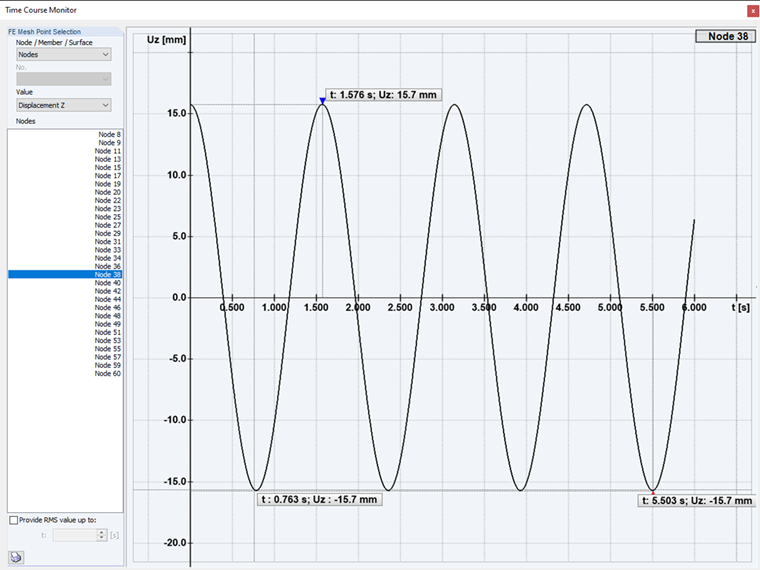
Se questo rapporto di frequenza è η < 1, che è indicato come eccitazione subcritica, la vibrazione forzata è più lenta della vibrazione naturale smorzata e si verifica un processo transitorio. Dopo alcuni brevi periodi di vibrazione naturale smorzata, il sistema è sintonizzato sulla vibrazione forzata più lenta, che alla fine rimane l'unica componente di vibrazione.
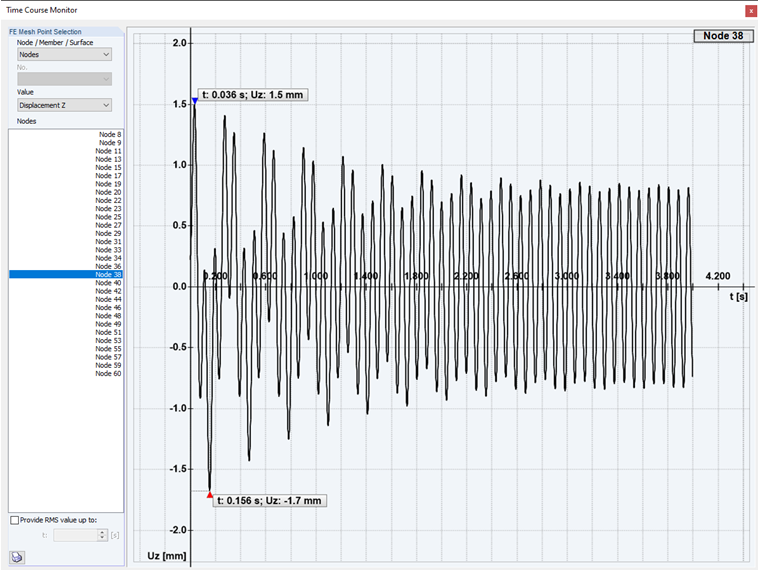
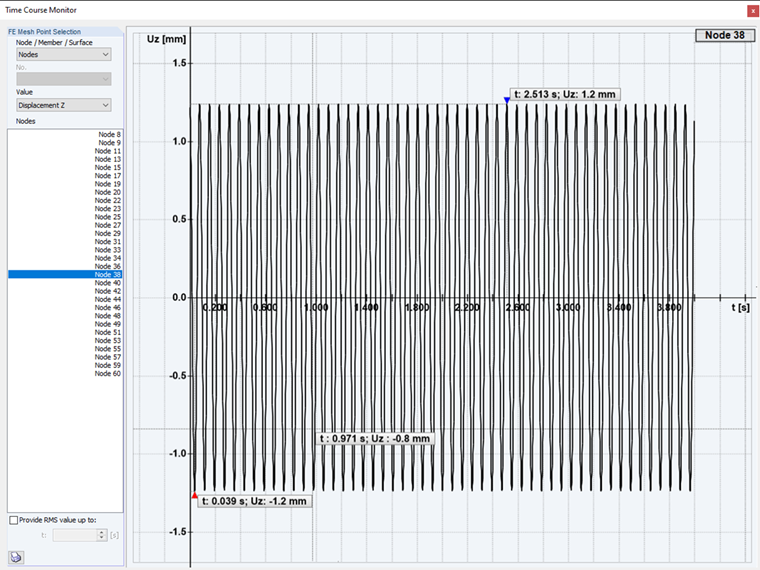
Se il caso è η > 1, ora chiamato eccitazione supercritica, la vibrazione forzata ha una frequenza maggiore della vibrazione naturale smorzata. Ora, l'oscillazione armonica veloce si verifica attorno all'oscillazione naturale più lenta e smorzata fino a quando non è completamente svanita, e di nuovo rimane solo la componente di vibrazione forzata dall'eccitazione.
Poiché c'è uno smorzamento in tutti i casi che si verificano praticamente, che porta allo sbiadimento naturale della vibrazione, è solo interessante, indipendentemente dal rapporto di frequenza, considerare e analizzare ulteriormente il movimento di vibrazione forzato rispettivamente rimanente (parte in stato stazionario). Questo movimento vibrazionale è chiamato vibrazione (quasi) stazionaria e lo stato corrispondente del sistema è chiamato stato stazionario.
La vibrazione naturale ha la frequenza angolare ωD del sistema smorzato, mentre la componente di vibrazione forzata dall'eccitazione ha la frequenza angolare ω dell'eccitazione armonica. Quindi la vibrazione complessiva, che risulta dalla sovrapposizione di queste due vibrazioni parziali, segue un andamento il cui aspetto dipende fortemente dal rapporto ω/ωD ; cioè sul rapporto di frequenza η.
Esempio
Il comportamento transitorio è descritto nel testo seguente, utilizzando una struttura in acciaio. Si presume che questa struttura sia eccitata armonicamente. Nella struttura, vengono generate eccitazioni armoniche per mostrare i diversi processi transitori. Al fine di sintonizzare meglio la frequenza di eccitazione armonica's alla struttura, viene prima creato un caso di vibrazione naturale mediante il modulo aggiuntivo DYNAM Pro - Natural Vibrations. Come semplificazione, nei casi di vibrazione naturale sono considerate solo le forme modali nella direzione Z globale.
Eccitazione subcritica: Nel primo caso dell'analisi time history, viene eseguita un'eccitazione subcritica della struttura. Con una frequenza di eccitazione inferiore alla forma modale.
Eccitazione supercritica: Nel secondo caso dell'analisi time history, viene eseguita un'eccitazione supercritica della struttura. Con una frequenza di eccitazione superiore alla forma modale.
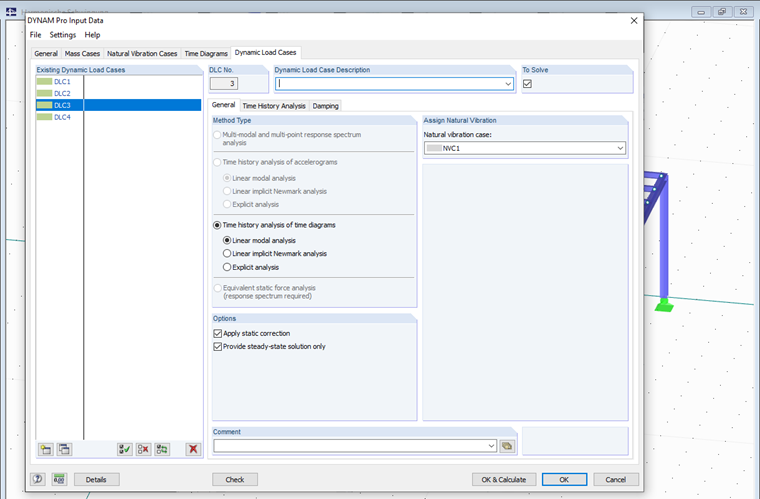
Nel terzo e nel quarto caso, utilizziamo l'opzione del modulo aggiuntivo per una soluzione in stato stazionario per entrambi i casi di eccitazione creati in precedenza. In questo modo, lo stato stazionario viene impostato direttamente. È anche generalmente indicato come stato stazionario.
