Теоретические основы
Колебательное движение первоначально невозмущенной, а затем гармонически возбуждаемой механической системы состоит из затухающих собственных колебаний с уменьшающейся амплитудой и вынужденного колебания с постоянной амплитудой. Процесс установления колебаний и установившееся состояние затем отражены в следующей формуле.
| t | Время |
| ω | Угловая частота возбуждения |
| ωd | угловая частота |
| ζ | затухание |
| I | Постоянная |
| B | Постоянная |
| C | Постоянная |
| d | Постоянная |
| η | Соотношение частот |
| γM0 | Частичный коэффициент надежности по прочности сечения |
| ωd | угловая частота |
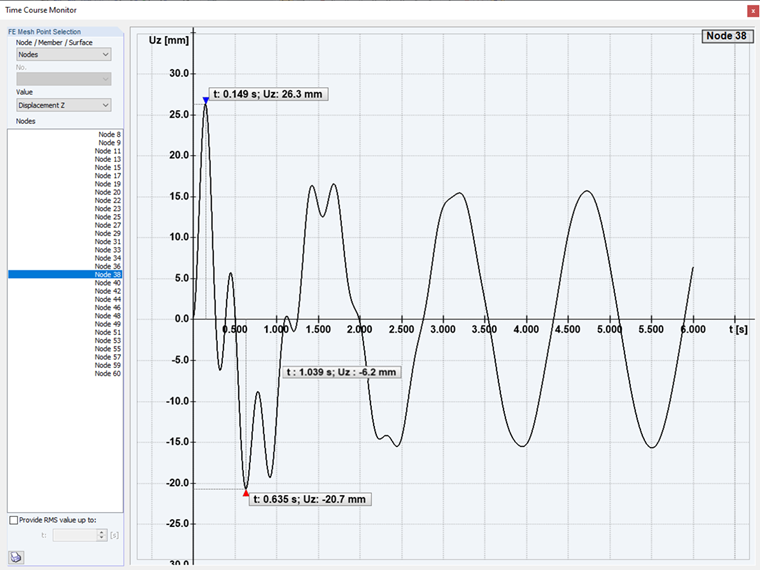
Если соотношение частот η < 1, то речь идет о докритическом возбуждении, т. е. вынужденное колебание медленнее затухающего собственного колебания и возникает процесс установления колебаний. После нескольких быстрых периодов затухающих собственных колебаний система устанавливается на более медленное вынужденное колебание, которое остается единственной составляющей колебаний.
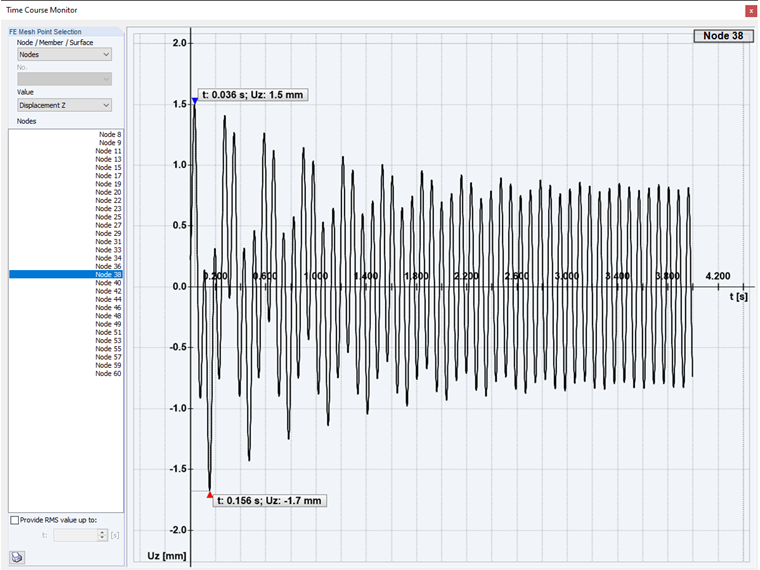
В случае, если η > 1, который называется сверхкритическим возбуждением, вынужденное колебание будет по частоте выше, чем затухающие собственные колебания. Тогда происходят быстрые гармонические колебания наряду с более медленным, затухающим собственным колебанием, пока оно полностью не затихнет и снова останется только составляющая колебания, вызванная возбуждением.
Поскольку во всех встречающихся на практике случаях присутствует затухание, которое приводит к окончанию собственных колебаний, то независимо от соотношения частот интерес представляет расчет и анализ остаточного движения вынужденных колебаний (установившейся составляющей). Данное колебательное движение обозначается как (квази)установившееся, а соответствующее состояние системы как установившееся состояние.
Собственное колебание имеет круговую частоту ωD затухающей системы, а составляющая вынужденных возбуждением колебаний - круговую частоту ω гармонического возбуждения. Общее колебание, возникающее в результате наложения этих двух частичных колебаний, имеет форму, характер которой сильно зависит от соотношения ω/ωD, то есть от соотношения частот η.
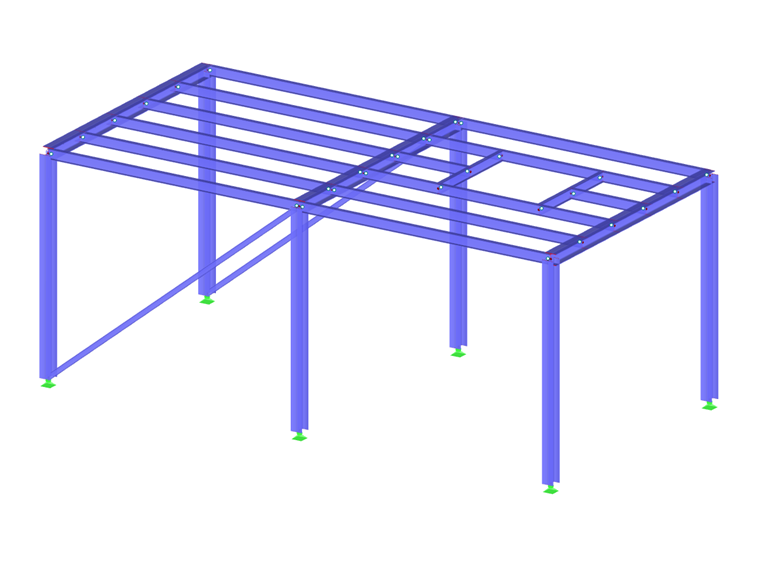
Пример
Параметры установления колебаний мы объясним на примере следующей стальной конструкции. Предполагается, что данная конструкция подвергается гармоническому возбуждению. Поэтому в конструкции формируются гармонические возбуждения для отображения различных процессов установления колебаний. Для лучшего соответствия частоты гармонического возбуждения данной конструкции создадим сначала случай собственных колебаний в модуле DYNAM Pro - Natural Vibrations. В рамках упрощения затем в случае собственных колебаний будут рассматриваться только собственные формы в общем направлении Z.
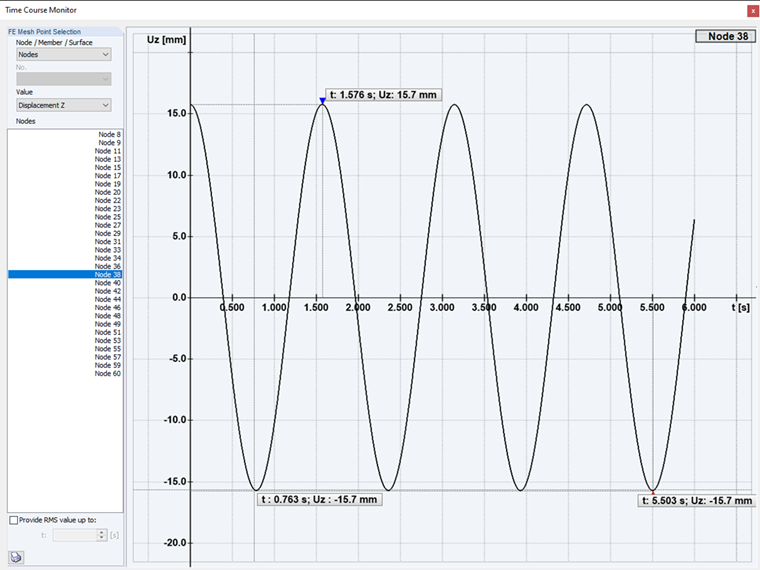
Докритическое возбуждение: В первом случае в анализе изменения параметров во времени выполняется так называемое докритическое возбуждение конструкции. С частотой возбуждения ниже, чем собственная форма.
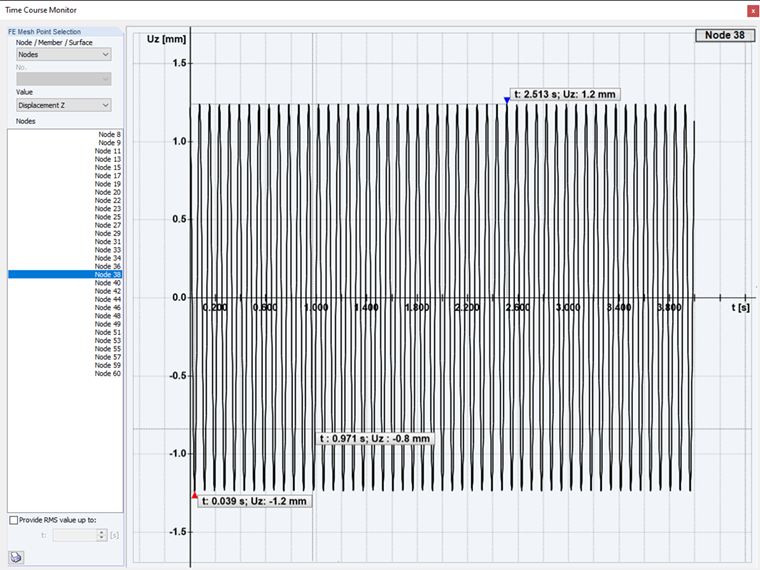
Сверхкритическое возбуждение: Во втором случае в анализе изменения параметров во времени используется так называемое сверхкритическое возбуждение конструкции. С частотой возбуждения выше, чем собственная форма.
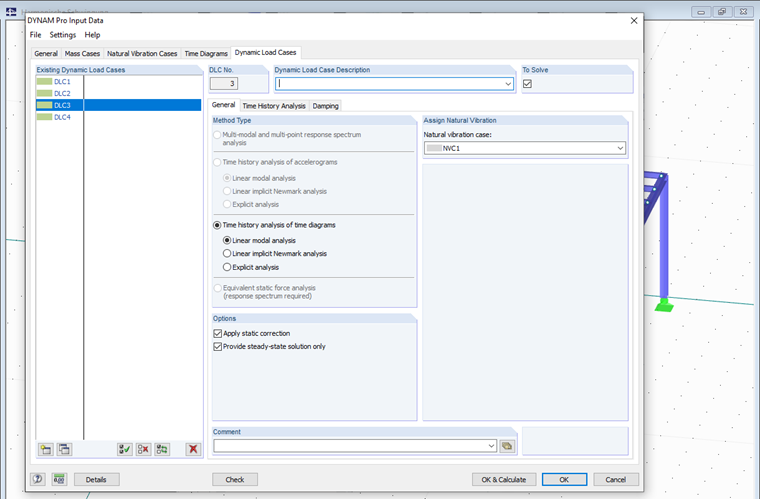
В третьем и четвертом случае в модуле DYNAM Pro - Forced Vibrations применяется вариант установившихся реакций для обоих ранее созданных случаев возбуждения. При этом напрямую задается стационарное состояние. Оно обычно также обозначается как установившееся состояние.
