理论背景
从最初的不受扰动的，然后是简谐激振的机械系统开始，它的振动由阻尼的振幅减小的固有振动和振幅恒定的强迫振动组成。 瞬态过程和稳态过程用下面的公式描述。
如果该频率比 η < 1，称为亚临界激励，强迫振动慢于阻尼的固有振动，并且出现一个瞬态过程。 在几个快速的阻尼自振周期之后，系统进入较慢的强迫振动阶段，这最终仍然是唯一的振动部分。
如果振型 η > 1，即超临界振型，则强迫振动的频率高于阻尼的固有振动频率。 现在，围绕较慢的、受阻尼的固有振动进行快速的谐振动，直到它完全减弱，只剩下由激励引起的振动分量。
因为在所有实际出现的情况下都存在阻尼，这会导致固有振动减弱，所以不管频率比如何，只有有意义的是分别考虑和分析剩余的强迫振动（稳态部分）。 这种系统的振动称为（准）稳态，相应的系统状态称为稳态。
自振的角频率为 ωD ，阻尼系统的角频率为 ω D 。 因此，总振动是这两个部分振动的叠加，其外观与ω/ωD密切相关。 ，即频数 η 。
示例
下文使用一个钢结构来说明该结构的瞬态特性。 假设该结构为简谐激振结构。 用户可以设置简谐激励来模拟不同的瞬态过程。 为了使结构的谐激励的频率更好地协调，首先使用附加模块 DYNAM Pro - 固有振动创建一个固有振动工况。 作为简化设计，在固有振动工况中只考虑全局 Z 方向上的振型。
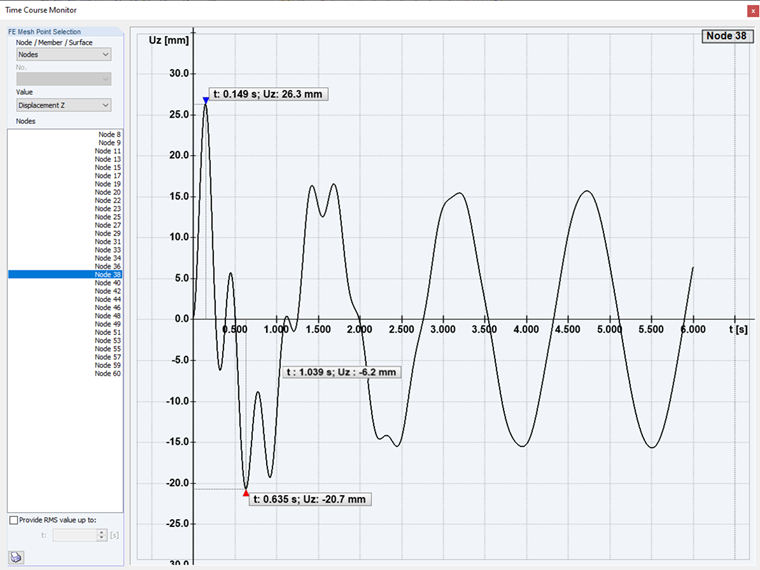
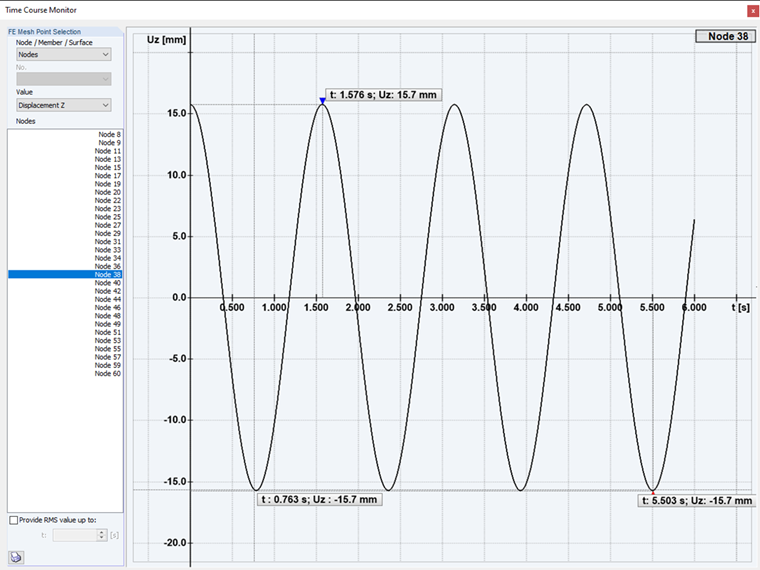
亚临界激振： 使用时程分析，可以考虑在第一种情况下，结构在亚临界激振作用下进行计算。 激励频率低于振型。
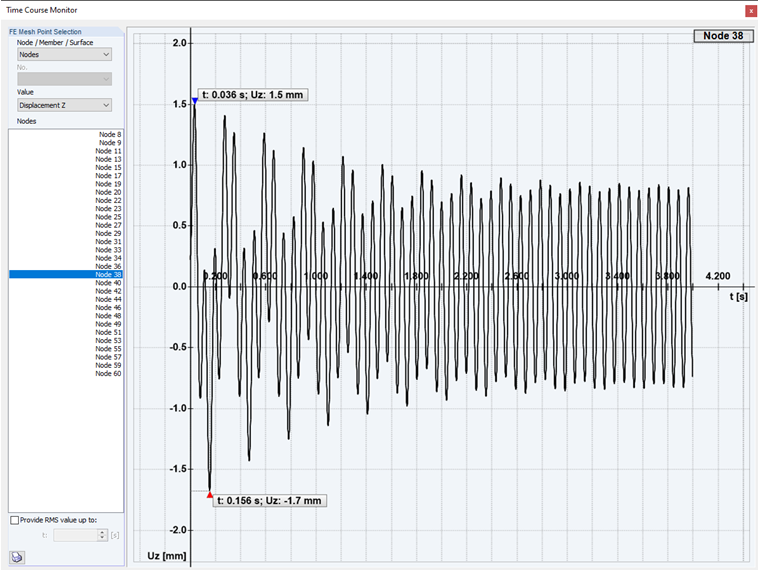
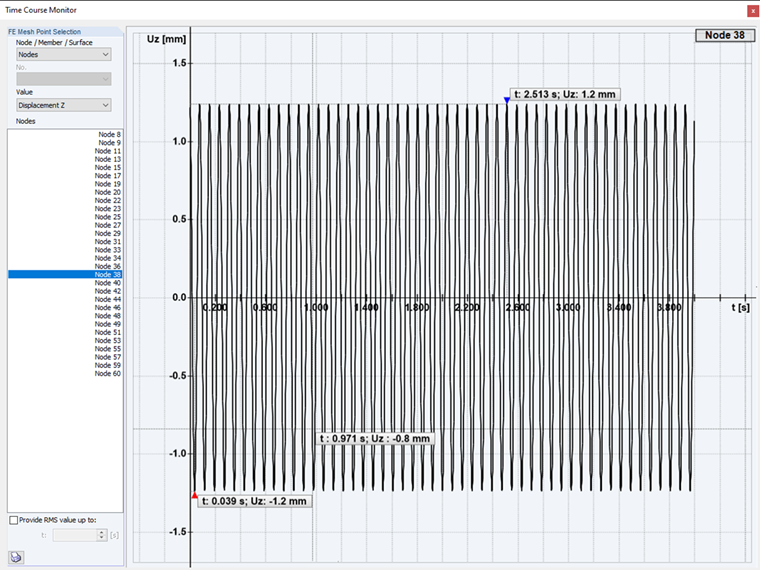
超临界激振： 第二种时程分析工况是对结构进行超临界激励， 激励频率高于振型。
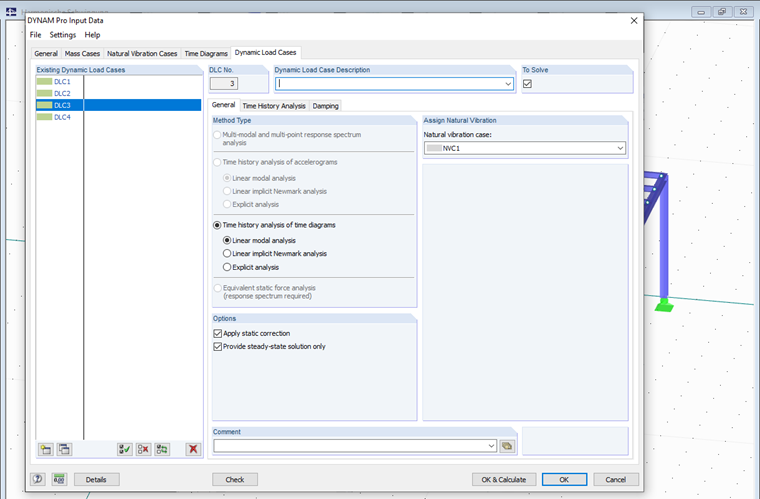
第三和第四种情况是我们之前创建的稳态解的附加模块选项。 程序默认设置为静态。 通常也称为稳态。
